A net of arectangular pyramidis shown. Therectangular base haslength 24 cm andwidth 21 cm. Thenet of the pyramidhas length 69.2 cmand width 64.6 cm.Find the surfacearea of the pyramid.
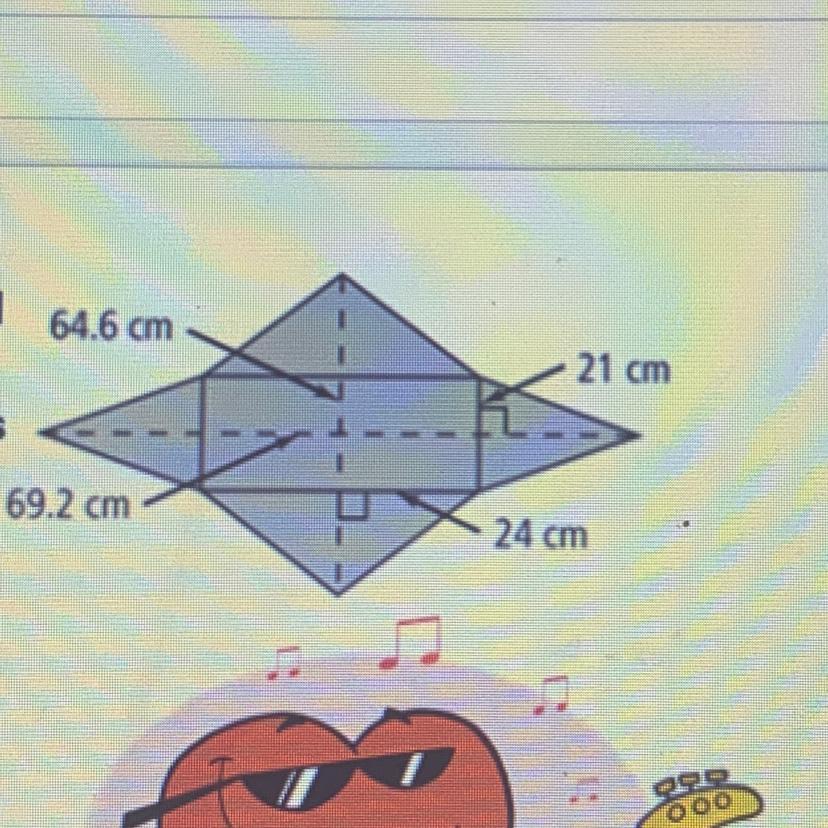
Answers
Solution
The Image will be of help
To find x
[tex]\begin{gathered} x+24+x=69.2 \\ 2x+24=69.2 \\ 2x=69.2-24 \\ 2x=45.2 \\ x=\frac{45.2}{2} \\ x=22.6 \end{gathered}[/tex]To find y
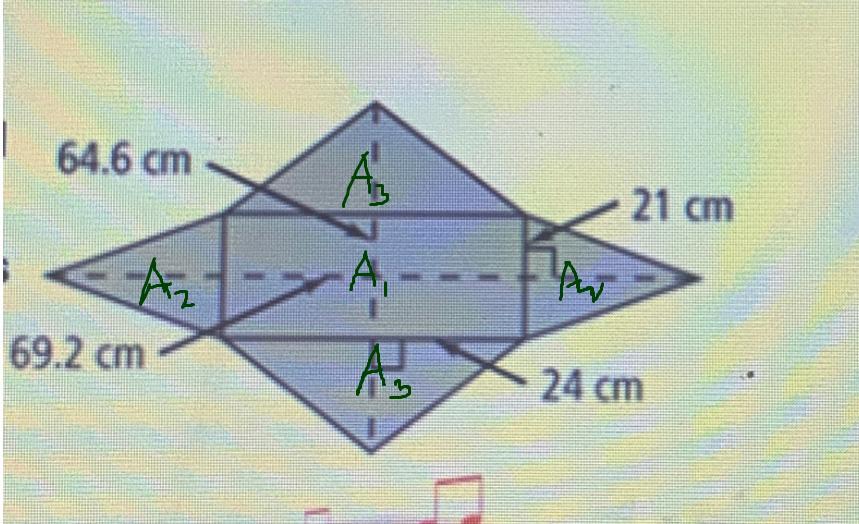
[tex]\begin{gathered} y+21+y=64.6 \\ 2y+21=64.6 \\ 2y=64.6-21 \\ 2y=43.6 \\ y=\frac{43.6}{2} \\ y=21.8 \end{gathered}[/tex]The diagram below will help us to find the Surface Area of the Pyramid
The surface area is
[tex]SurfaceArea=A_1+2A_2+2A_3[/tex]To find A1
[tex]A_1=24\times21=504[/tex]To find A2
[tex]\begin{gathered} A_2=\frac{1}{2}b\times h \\ 2A_2=b\times h \\ 2A_2=21\times22.6 \\ 2A_2=474.6 \end{gathered}[/tex]To find A3
[tex]\begin{gathered} A_3=\frac{1}{2}bh \\ 2A_3=b\times h \\ 2A_3=24\times21.8 \\ 2A_3=523.2 \end{gathered}[/tex]The surface Area
[tex]\begin{gathered} SurfaceArea=A_1+2A_2+2A_3 \\ SurfaceArea=504+474.6+523.2 \\ SurfaceArea=1501.8cm^2 \end{gathered}[/tex]Thus,
[tex]SurfaceArea=1501.8cm^2[/tex]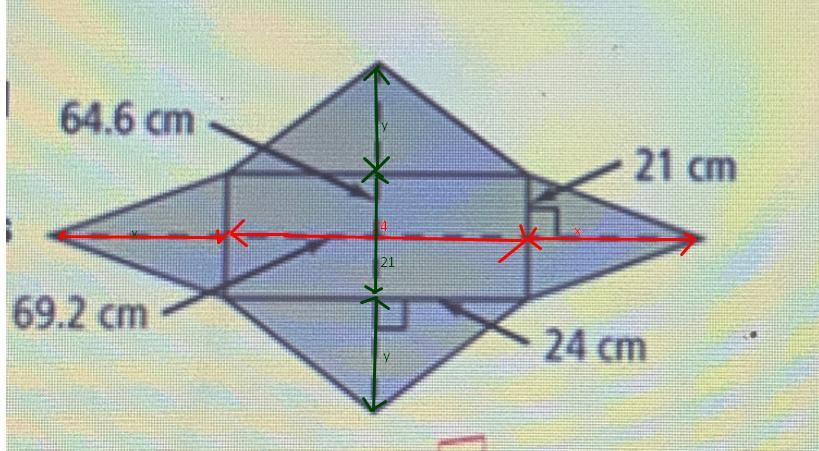
Related Questions
Good morning, I need help on this questions. Thanks :)
Answers
The observed values are given in the table shown in the question. The line of best fit is given to be:
[tex]y=-1.1x+90.31[/tex]where x is the average monthly temperature and y is the heating cost.
A residual is a difference between the observed y-value (from scatter plot) and the predicted y-value (from regression equation line). The formula will be:
[tex]Residual=Observed\text{ }y\text{ }value-Predicted\text{ }y\text{ }value[/tex]QUESTION A
The average monthly temperature is 24.9:
[tex]x=24.9[/tex]Observed cost:
[tex]y=51.00[/tex]Predicted cost:
[tex]\begin{gathered} y=-1.1(24.9)+90.31=-27.39+90.31 \\ y=62.92 \end{gathered}[/tex]Residual:
[tex]\begin{gathered} R=51.00-62.92 \\ R=-11.92 \end{gathered}[/tex]QUESTION B
The average monthly temperature is 35.9:
[tex]x=35.9[/tex]Observed cost:
[tex]y=67.00[/tex]Predicted cost:
[tex]\begin{gathered} y=-1.1(35.9)+90.31=-39.49+90.31 \\ y=50.82 \end{gathered}[/tex]Residual:
[tex]\begin{gathered} R=67.00-50.82 \\ R=16.18 \end{gathered}[/tex]Answer: Hl
Step-by-step explanation:
If f(x) = -3 and g(x) = 4x + 2x - 4, find (* + )(x).O A. 4x2 + x +1OB. 432 + x ->C.X2-12OD. 4x2+2x-7
Answers
You have the following functions:
[tex]\begin{gathered} f(x)=\frac{x}{4}-3 \\ g(x)=4x^2+2x-4 \end{gathered}[/tex]In order to find (g + f)(x) add like terms of each function. Remind that like terms are those terms with the same variable and same exponent.
Then, you have:
[tex]\begin{gathered} (f+g)(x)=4x^2+2x+\frac{x}{4}-3-4 \\ (f+g)(x)=4x^2+\frac{9}{4}x-7 \end{gathered}[/tex]Hence, the answer is
4x^2 + 9/4 x - 7
The diagram has a hollow cylindrical tube, of internal radius 4cm and external radius 6cm. How can I determine the area of an external curved surface, how can I get the area of the inner curved surface and how can I get the total surface area of the tube?
Answers
Given:
internal radius = 4cm
External radius = 6cm
Height = 20cm
Curved surface area of the external surface
The formula for the curved surface is:
[tex]\begin{gathered} =2\pi rh \\ \text{Where r is a radius} \\ \text{and h is the height of the cylinder} \end{gathered}[/tex]Hence, the curved surface area:
[tex]\begin{gathered} C\mathrm{}S\mathrm{}A\text{ of external surface = 2}\times\pi\times6\times20 \\ =753.982cm^2 \end{gathered}[/tex]Curved surface area of the inner surface:
[tex]\begin{gathered} C\mathrm{}S\mathrm{}A\text{ of inner surface = 2 }\times\pi\times4\times\text{ 20} \\ =502.654cm^2 \end{gathered}[/tex]The total surface area of the tube :
The total surface area can be found using the formula:
[tex]\text{Total Surface area = }2\pi(R^2-r^2)\text{ + }2\pi h(R\text{ + r)}[/tex]Where R is the radius of the external surface and r is the radius of the inner surface
Hence:
[tex]\begin{gathered} \text{Total Surface area = 2}\times\pi\times(6^2-4^2)\text{ + 2}\times\pi\times20\times(6\text{ + 4)} \\ =\text{ }1382.3cm^2 \end{gathered}[/tex]I need help with my homework pls be fast it’s 11pm for me and I couldn’t do this earlier because of family business
Answers
We have a linear function and we have to find the meaning of the slope.
The function is:
[tex]C=50h+35[/tex]In this function the slope is m=50, as it is the coefficient for h, the number of hours.
The slope usually represents the variation of the result variable (in this case, the cost in dollars) and the independent variable (in this case, h, the number of hours).
Then, we can think of the slope in this model as the marginal hourly rate he charges. This means that any additional hour of work will cost $50 more.
Then, from the options given, the correct one is: the charge per hour [Option D].
Consider the following data. The expected value is -2.1.Find the variance, standard deviation, P(X ≥ -1), and P(X ≤ -3).
Answers
Given
The data,
To find:
The variance, standard deviation, P(X ≥ -1), and P(X ≤ -3).
Explanation:
It is given that,
Then,
The variance is,
[tex]\begin{gathered} Var[x]=(-4-(-2.1))^2\times0.2+(-3-(-2.1))^2\times0.3+(-2-(-2.1))^2 \\ \times0.1+(-1-(-2.1))^2\times0.2+(0-(-2.1))^2\times0.2 \\ =(-4+2.1)^2\times0.2+(-3+2.1)^2\times0.3+(-2+2.1)^2\times0.1+(-1+2.1)^2 \\ \times0.2+(2.1)^2\times0.2 \\ =3.61\times0.2+0.81\times0.3+0.01\times0.1+1.21\times0.2+4.41\times0.2 \\ =0.722+0.243+0.001+0.242+0.882 \\ =2.09 \end{gathered}[/tex]And the standard deviation is,
[tex]\begin{gathered} SD=\sqrt{Var[x]} \\ =\sqrt{2.09} \\ =1.45 \end{gathered}[/tex]Also,
[tex]\begin{gathered} P\left(X≥-1\right)=P(X=-1)+P(X=0) \\ =0.2+0.2 \\ =0.4 \\ P\left(X≤-3\right)=P(-4)+P(-3) \\ =0.2+0.3 \\ =0.5 \end{gathered}[/tex]Hence, the answers are,
Variance is 2.09
Standard deviation is 1.45
P(X ≥ -1) is 0.4
P(X ≤ -3) is 0.5.
write each decimal in word form 302.78 and 15.023
Answers
Answer and Explanation:
302.78 can be written as THREE HUNDRED AND TWO AND SEVENTY EIGHT HUNDREDTHS or THREE HUNDRED AND TWO POINT SEVEN EIGHT.
15.023 can be written in word as FIFTEEN AND TWENTY THREE THOUSANDTHS or FIFTEEN POINT ZERO TWO THREE.
Solve the equation for y in terms of x. After that, replace y & solve with function notation f(x). Once you solve that, find f(4).y+3x^2=4f(x)=____f(4)=____
Answers
Given:
[tex]y+3x^2=4[/tex]We have that y f(x), so solve for f(x):
[tex]\begin{gathered} y+3x^2-3x^2=4-3x^2 \\ y=4-3x^2 \\ f(x)=4-3x^2 \end{gathered}[/tex]And for f(4):
[tex]f(4)=4-3(4)^2=4-3(16)=4-48=-44[/tex]Answer:
[tex]\begin{gathered} f(x)=4-3x^{2} \\ f(4)=-44 \end{gathered}[/tex]Amy's cookie shop had expenses of the following: flour $45.00sugar $92.00butter $53 she earns $12 per dozen. what is her profit,if she sells 9 dozen?what is the total dollar amount for expenses?what is the total dollar amount for earnings or revenue?
Answers
If she earns $12 per dozen, the following will be the profit if she sells 9 dozen:
[tex]9\cdot12=108[/tex]Profit would be $108.
*The dollar amount of expenses would be:
[tex]e=\frac{190\cdot108}{12}\Rightarrow e=1710[/tex]The expenses would be $1710 if she were to sell 9 dozen.
*The total amount of revenue would be $108 for the 9 dozen sold.
Yea I can see if it works if it’s okay
Answers
SOLUTION
We want to find the derivative of
[tex]y=sin(1.2t-3.7)[/tex](a) So, using chain rule, the inside function is u,
we have the inside:
[tex]u=1.2t-3.7[/tex]outside becomes
[tex]y=sin(u)[/tex](b) The derivative of
inside, we have
[tex]\frac{du}{dt}=1.2[/tex]derivative of the outside, we have
[tex]\frac{dy}{du}=cos(u)[/tex]chain rule we have
[tex]\begin{gathered} \frac{dy}{dt}=\frac{dy}{du}\times\frac{du}{dt} \\ =cos(u)\times1.2 \\ =cos(1.2t-3.7)\times1.2 \end{gathered}[/tex]Hence the answer is
[tex]\frac{dy}{dt}=1.2cos(1.2t-3.7)[/tex]Check off all of the equations that would give infinitely many solution
Answers
All of the equations that would give infinitely many solutions are given as follows:
[tex]\begin{gathered} 1)\text{ 3x + 12 = 3x + 12} \\ 2)\text{ 2\lparen3x - 4\rparen = 6x - 8} \end{gathered}[/tex]Thus the correct answer is option 3 and option 5.
A Ferris wheel at a carnival has a diameter of 72 feet. Suppose a passenger is traveling at 5 miles per hour. (A useful fact: =1mi5280ft.)
(a) Find the angular speed of the wheel in radians per minute.
(b) Find the number of revolutions the wheel makes per hour. (Assume the wheel does not stop.)
Answers
a) The Ferris wheel has an angular speed is 12.222 radians per minute.
b) The Ferris wheel makes 116.712 revolutions in an hour.
How to understand and analyze the kinematics of a Ferris wheel
Kinematics is a branch of mechanical physics that studies the motion of objects without considering its causes. In other words, kinematics studies displacements, velocities and accelerations in translation, rotation and combined motion. In this case we find a Ferris wheel rotating around its axis at constant rate.
a) Then, the angular speed (ω), in radians per minute, is determined by the following product:
ω = v / R
Where:
v - Linear velocity at the rim of the Ferris wheel, in feet per second.R - Radius of the Ferris wheel, in feet.Please notice that the length of the radius is the half of the length of the diameter.
If we know that v = 5 mi / h and R = 36 feet, then the angular speed of the wheel is:
ω = [(5 mi / h) · (1 h / 60 min) · (5280 ft / 1 mi)] / [(0.5) · (72 ft)]
ω = 12.222 rad / min
The angular speed is 12.222 radians per minute.
b) A revolution is equal to an angular displacement of 2π radians and an hour is equal to 60 minutes. Then, we can derive the number of revolutions in an hour by dimensional analysis:
n = (12.222 rad / min) · (1 rev / 2π rad) · (60 min / h)
n = 116.712 rev / h
There are 116.712 revolutions in an hour.
To learn more on Ferris wheels: https://brainly.com/question/16396069
#SPJ1
in a hurry! have to finish the practice test in 30mins, so I can take the real one!(CHECKING AWNSERS, SO ONLY NEED AWNSERS TO I CAN COMPARE)
Answers
The expression can be simplified as,
[tex]\begin{gathered} \frac{3}{x+2}+\frac{2}{x-3}=\frac{3(x-3)+2(x+2)}{(x-3)(x+2)} \\ =\frac{3x-9+2x+4}{(x-3)(x+2)} \\ =\frac{5x-5}{(x-3)(x+2)} \end{gathered}[/tex]Thus, option (D) is the correct option.
–2(1 – 5x) = 4 – 4(-2x)
Answers
-2(1 - 5x) = 4 - 4(-2x)
First, we eliminate the parentheses and solve the multiplications
-2*1 - 2*(-5x) = 4 + 8x
-2 + 10x = 4 + 8x
Now, we subtract 8x from both sides and add 2 to both sides
-2 + 10x - 8x + 2 = 4 + 8x - 8x + 2
2x = 6
Then, we divide both sides by 2
2x/2 = 6/2
x = 6/2
x = 3
a test has 20 Questions worth 100 points the test consists of true or false questions worth 3 points each and multiple choice questions worth 11 points each how many multiple choice questions are on the test
Answers
A test is to be conducted with certain types of questions and each type of question weighs certain number of points.
A test would consist of two types of questions. These two types will be assigned variables that will denote the number of questions respectively as follows:
[tex]\begin{gathered} \text{True and False: x} \\ \text{MCQS : y} \end{gathered}[/tex]We are given that the entire test will consits of 20 questions. We can express the total number of questions on the test in terms of number of True and False questions ( x ) and number of MCQS ( y ) as follows:
[tex]\begin{gathered} \text{Total number of Questions = True and False + MCQS} \\ \textcolor{#FF7968}{20}\text{\textcolor{#FF7968}{ = x + y }}\textcolor{#FF7968}{\ldots Eq1} \end{gathered}[/tex]Further information is given to us in the questions regarding the number of points aloted to each type. The total weightage of each type of question on the test can be expressed as a product of ( number of each type * point weight of each type ).
The point weights for each type of questions are:
[tex]\begin{gathered} \text{True and False ( x ) : 3 points each} \\ \text{MCQs ( y ) : 11 points each} \end{gathered}[/tex]The total weights of each types of questions are:
[tex]\begin{gathered} \text{True and False ( points ) = 3}\cdot x \\ \text{MCQS ( points ) = 11}\cdot x \end{gathered}[/tex]We are given that the entire test is worth ( 100 points ). We express the total number of points of the test in terms of total weight of each type of question as follows:
[tex]\begin{gathered} test\text{ points = True and False ( points ) + MCQS ( points )} \\ \textcolor{#FF7968}{100}\text{\textcolor{#FF7968}{ = 3}}\textcolor{#FF7968}{\cdot x}\text{\textcolor{#FF7968}{ + 11}}\textcolor{#FF7968}{\cdot y\ldots}\text{\textcolor{#FF7968}{ Eq2}} \end{gathered}[/tex]We have two equations that express the total number of questions ( Eq 1 ) and total points ( Eq2 ) of the test in terms of number of True and False questions ( x ) and number of MCQs on the test ( y ).
[tex]\begin{gathered} \textcolor{#FF7968}{x}\text{\textcolor{#FF7968}{ + y = 20 }}\textcolor{#FF7968}{\ldots Eq1} \\ \textcolor{#FF7968}{3x}\text{\textcolor{#FF7968}{ + 11y = 100 }}\textcolor{#FF7968}{\ldots}\text{\textcolor{#FF7968}{ Eq2}} \end{gathered}[/tex]We will solve the above two equations simultaneously using Elimination method.
Step1: Multiply Eq1 with ( -3 )
[tex]\begin{gathered} -3\cdot\text{ ( x + y ) = -3}\cdot20 \\ \textcolor{#FF7968}{-3x}\text{\textcolor{#FF7968}{ - 3y = -60 }}\textcolor{#FF7968}{\ldots}\text{\textcolor{#FF7968}{ Eq3}} \end{gathered}[/tex]Step2: Add Eq 3 into Eq 2
[tex]\begin{gathered} -3x\text{ - 3y = -60 } \\ 3x\text{ + 11y = 100} \\ =========== \\ 8y\text{ = 40 } \\ \textcolor{#FF7968}{y}\text{\textcolor{#FF7968}{ = 5}} \\ =========== \end{gathered}[/tex]Step3: Back susbtitue the value of ( y ) into ( Eq1 )
[tex]\begin{gathered} x\text{ + ( 5 ) = 20 } \\ \textcolor{#FF7968}{x}\text{\textcolor{#FF7968}{ = 15 }} \end{gathered}[/tex]Therefore, the number of each type of questions that must be put on the test should be.
[tex]\begin{gathered} \text{\textcolor{#FF7968}{True and False ( x ) = 15}} \\ \text{\textcolor{#FF7968}{MCQs ( y ) = 5}} \end{gathered}[/tex]3.615 x 4 regrouping
Answers
The perimeter of a rectangle is 36 cm and the length is twice the width. What are the dimensions of this rectangle? What’s the length and width?
Answers
Perimeter = 2x + 2x + x + x = 6x. 6x = 36, so x = 6. The rectangle is 6*12, so area = 72 sq cm.
INT. ALGEBRA: You have a coupon for $20 off the purchase of a calculator. At the same time, the calculator is offered with a discount of 20%, and no further discounts apply. For what price on the calculator do you pay the same amount for each discount?
Thank you for your help, and please do show work! I will be looking to give the Brainliest answer to someone!
Answers
Chen is opening a new account with a $1,200 deposit. She will be keeping money in the account, compounded monthly for no more than 3 years. the formula gives the value, V, of the account as a function of time, t. Which is a reasonable domain of this function?V(t)= 1,200(1 + 0.02)^t/12A) 0< or equal to t < or equal to 36B) 0C) 0 < or equal to t < or equal to 1,273.45D) 1,200 < or equal to t < or equal to 1,273.45
Answers
The Solution:
Given the function:
[tex]V(t)=1200(1+0.02)^{\frac{t}{12}}[/tex]We are required to find a reasonable domain for the given function.
The domain of the function V(t) is the range of values for t.
The question says Chen is will continue to keep money in the account for not more than 3 years, but the interest will be compound monthly.
Recall:
1 year = 12 months
So,
3 years will be
[tex]12\times3=36\text{ months}[/tex]This means that the range of values for t is:
[tex]0\leq t\leq36[/tex]Therefore, the correct answer is [option A]
Today's previewYou can solve this by rearranging to create asituation to use the method from the previouslesson, or you can solve this by thinking a littledifferently about how the variables below mightalso be described.... so solve it.y = 2x + 4x + y = 7
Answers
Let MF = 3x - 4 and BM = 5x - 5
Answers
Answer:
Explanation:
a)Here, we want to get the value of x
Mathematically, we know that for a triangle with median M, the length of one of the sides is two times the length of the other side of the median
We have this as:
[tex]BM\text{ }=\text{ 2MF}[/tex]Using the side lengths given, we have it that:
[tex]\begin{gathered} 5x-5\text{ = 2(3x-4)} \\ 5x-5\text{ = 6x-8} \\ 6x-5x=8-5 \\ x\text{ = 3} \end{gathered}[/tex]b) We want to find the length of MF. We just have to substitute the value of x in the expression for MP
Mathematically, we have this as:
[tex]MF\text{ = 3(3)-4 = 9-4 = 5}[/tex]c) We want to find the length of BM
[tex]5x-5\text{ = 5(3)-5 = 15-}5\text{ = 10}[/tex]d) Here, we want to find the length of BF
[tex]\begin{gathered} BF\text{ = BM + MF} \\ BF\text{ = 10 + 5 = 15} \end{gathered}[/tex]A ball is shot from a cannon into the air with an upward velocity of 40 ft/sec. The equation that give the height (h) of the ball at any time (t) is: h(t)= -16t^2 + 40t + 1.5. Find the maximum height attained by the ball. I need a clear explanation because I have to expose this
Answers
The height of the ball at any time t is given by
[tex]h(t)=-16t^2+40t+1.5[/tex]This is a quadratic equation, which attains its maximum value at time:
[tex]t=\frac{-b}{2a}[/tex]In the given equation, a = -16 and b = 40. substitute these values in the formula:
[tex]t=\frac{-40}{-16\times2}=\frac{-40}{-32}=\frac{5}{4}[/tex]Therefore, the ball attains its maximum height at t=5/4 seconds which is given below:
[tex]\begin{gathered} h(\frac{5}{4})=-16(\frac{5}{4})^2+40(\frac{5}{4})+1.5 \\ =-25+50+1.5 \\ =26.5 \end{gathered}[/tex]Thus, the maximum height attained by the ball is 26.5 feet.
Hello good night everyone I need help with number 6 I’m so lost I’m abt to cry
Answers
We have to add and substract this complex numbers.
In this type of problems, where we have to add or substract complex numbers, we need to have the real and imaginary terms separated.
In this case, we already have all the terms as real or imaginary.
Then, we can group the real terms on one side and the imaginary terms on the other side and simplify them. We can do it like this:
[tex]\begin{gathered} (7-2i)-(-1-4i)+3 \\ 7-2i+1+4i+3 \\ (7+1+3)+(-2i+4i) \\ 11+2i \end{gathered}[/tex]Answer: 11 + 2i
write the expression using exponents 7•7•7•7•7•7• (–3)•(–3)•(–3)•(–3)
Answers
We have the number 7 multiplying itself 6 times, and the number (-3) multiplying itself 5 times, so writing the expression using exponents, we have:
[tex]\begin{gathered} 7\cdot7\cdot7\cdot7\cdot7\cdot7=7^6 \\ (-3)\cdot(-3)\cdot(-3)\cdot(-3)\cdot(-3)=(-3)^5 \\ \\ 7\cdot7\cdot7\cdot7\cdot7\cdot7\cdot(-3)\cdot(-3)\cdot(-3)\cdot(-3)\cdot(-3)=7^6\cdot(-3)^5 \end{gathered}[/tex]So the final expression is 7^6 * (-3)^5
if you could please answer quickly my brainly app keeps crashing
Answers
In this case, we'll have to carry out several steps to find the solution.
Step 01:
Data:
diagram:
circle and chords
Step 02:
congruent chords:
Congruent chords are equidistant from the center of a circle.
x = 7 + 7
x = 14
The answer is:
x = 14
Solve the system by substitution:y=-6x-77x+y=-3(__ , __)
Answers
Substitute -6x-7 for y in the equation 7x+y=-3 to obtain the value of the of x.
[tex]\begin{gathered} 7x-6x-7=-3 \\ x=-3+7 \\ =4 \end{gathered}[/tex]Substitute 4 for x in the equation y=-6x-7 to obtain the value of the y.
[tex]\begin{gathered} y=-6\cdot4-7 \\ =-24-7 \\ =-31 \end{gathered}[/tex]So solution of the equation is (4,-31).
2) seperate 90 into two parts (the sum of two numbers is 90)so that one part Cone number) is four times the other part (the other number)
Answers
The sum of two parts equal 90.
Also,
one part is 4 times the other part.
Let the normal part be "x", so the 4 times part would be "4x".
Their sum is 90, thus we can write:
[tex]x+4x=90[/tex]Solving for x (a part):
[tex]\begin{gathered} x+4x=90 \\ 5x=90 \\ x=\frac{90}{5} \\ x=18 \end{gathered}[/tex]The other part is:
90 - 18 = 72
So,
The two parts we separate 90 into are "18 and 72".
A hummingbird's brain has a weight of approximately 2.94 x 10- ounces. An elephant's brain has a weight ofapproximately 1.76 x 102 ounces.Approximately how many times heavier is the elephant's brain than the hummingbird's brain?A) 60B) 600C) 6,000D) 60,000
Answers
Given the information on the problem,we have to divide the weight of the elephant's brain by the weight of the bird's brain, then, using the rules of exponents, we have the following:
[tex]undefined[/tex]in the sophomore class at Summit High School the number of students taking French is 2/3 of the number taking Spanish. how many students are studying each language if the total number of students in French and Spanish is 310 ?This is Homework
Answers
From the information given in the statement let be
[tex]\begin{gathered} f=\frac{2}{3}s\text{ (1)} \\ f+s=310\text{ (2)} \end{gathered}[/tex]Where
*f: number of students taking a French class
*s: number of students taking a Spanish class
So, you have a system of linear equations, which you can use the substitution method.
To do this, replace the value of the first equation in the second equation and solve for s
[tex]\begin{gathered} f+s=310\text{ (2)} \\ \frac{2}{3}s+s=310 \\ \frac{5}{3}s=310 \\ \text{ Multiply by }\frac{3}{5}\text{ on both sides of the equation} \\ \frac{3}{5}\cdot\frac{5}{3}s=310\cdot\frac{3}{5} \\ s=186 \end{gathered}[/tex]Now,
What is the quotient of 2.592 x 10^7 and 7.2 x 10^4 expressed in scientific notation?
Answers
Answer:
Explanation:
Given the expression:
[tex]\frac{2.592\times10^7}{7.2\times10^4}[/tex]We can rewrite it as:
[tex]\frac{2592\times10^{-3}\times10^7}{72\times10^{-1}\times10^4}[/tex]Combine all powers of 10:
[tex]\begin{gathered} =\frac{2592\times10^{-3+7}}{72\times10^{-1+4}^{}} \\ =\frac{2592\times10^4}{72\times10^3} \\ =\frac{2592}{72^{}}\times\frac{10^4}{10^3} \\ =36\times10 \\ =3.6\times10^1\times10^1 \\ =3.6\times10^{1+1} \\ =3.6\times10^2 \end{gathered}[/tex]The quotient expressed in scientific notation is 3.6 x 10².
Mario ordered a pizza for dinner. WHEN IT Came Mario quickly ate 1/8 of the pizza. While Mario was getting napkins, his pet poodle ate 1/3 of the pizza.
Answers
Mario ordered a pizza for dinner. when pizza came, Mario quickly ate 1/8 of the pizza and his pet ate 1/3 of the pizza, then the remaining fraction of pizza left is 13/24
The fraction of pizza that Mario eat = 1/8
The fraction of pizza that his pet eat = 1/3
Total fraction = (1/8) + (1/3)
= 11/24
The remaining fraction of pizza = 1 - 11/24
= 13/24
Hence, Mario ordered a pizza for dinner. when it came, Mario quickly ate 1/8 of the pizza and his pet ate 1/3 of the pizza, then the remaining fraction of pizza left is 13/24.
The complete question is :
Mario ordered a pizza for dinner. When it Came Mario quickly ate 1/8 of the pizza. While Mario was getting napkins, his pet poodle ate 1/3 of the pizza. What is the fraction of pizza that left?
Learn more about fraction here
brainly.com/question/2115640
#SPJ1