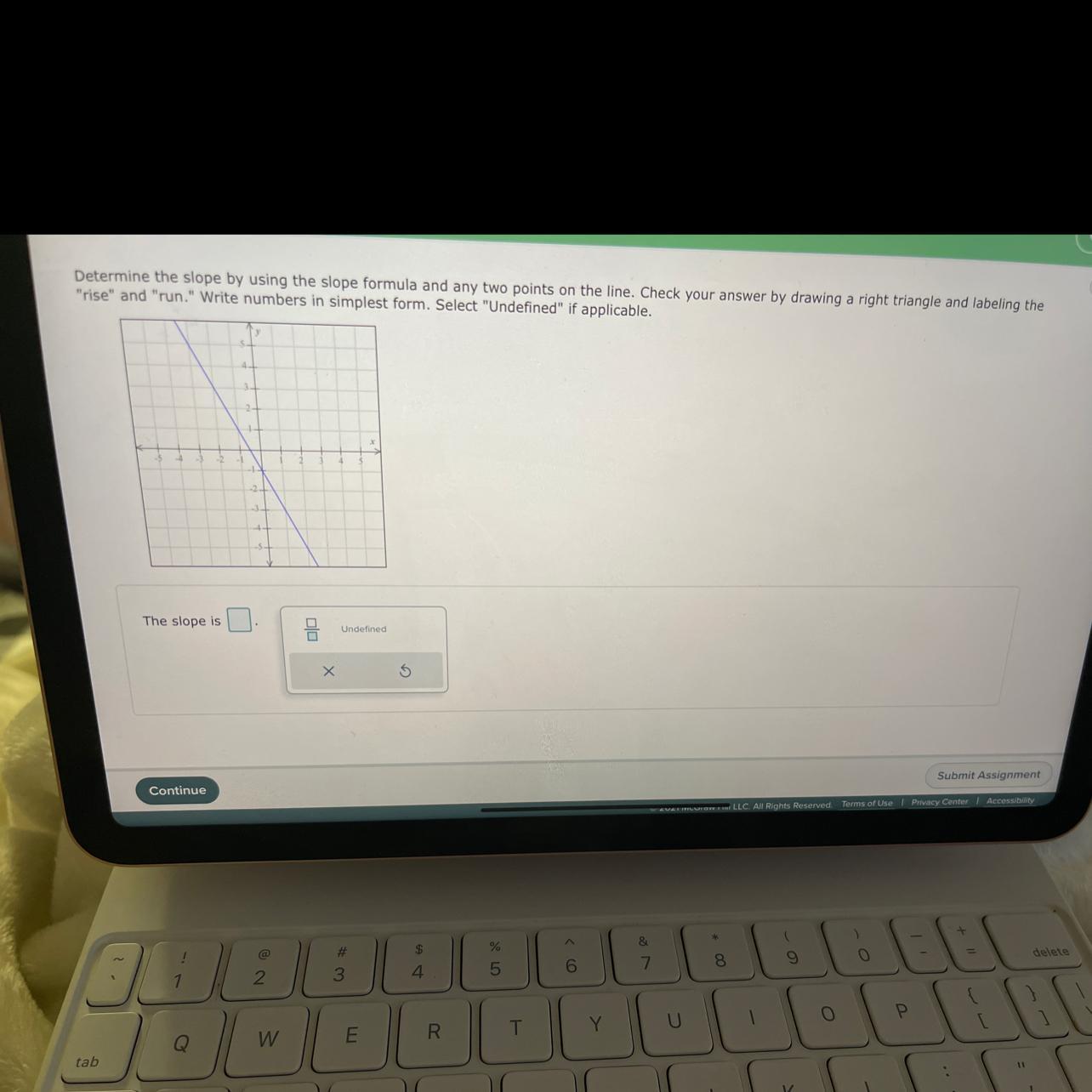
Determine the slope by using the slope formula and add two points on the line check your answer by drawing a right triangle and labeling the rise and run right numbers in simplest form select undefined if Applicable
Answers
Answer:
The slope is -2
Explanation:
The slope can be calculated as
[tex]m=\frac{y_2-y_1}{x_2-x_1}[/tex]Where (x1, y1) and (x2, y2) are the coordinates of two points in the line.
Replacing (x1, y1) by ( 0, -1) and (x2, y2) by (1, -3), we get:
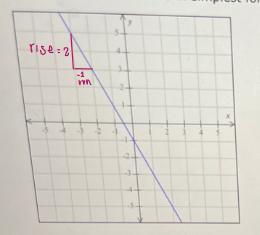
[tex]m=\frac{-3-(-1)}{1-0}=\frac{-3+1}{1}=\frac{-2}{1}=-2[/tex]Now, we can check the answer using the following drawing
Since rise over run is also equal to 2/(-1) = -2. We can say that the slope is -2.
Related Questions
algebra 2 question..
Answers
We are supposed to solve the equation
[tex]6(2x-1)-12=3(7x+4)[/tex]Here, we need to apply the distributive laws on both sides.
Comment: The distributive laws say that
[tex]a(b+c)=ab+ac\text{ and }(b+c)a=ba+ca[/tex]Using this comment we get
[tex]6(2x-1)=6(2x)+6(-1)=12x-6[/tex][tex]3(7x+4)=3(7x)+3(4)=21x+12[/tex]Then, our equation becomes
[tex](12x-6)-12=21x+12[/tex][tex]12x-18=21x+12[/tex]Now, let's apply the rule: terms with x on the right-hand side, and the rest on the left-hand side, to obtain
[tex]-18-12=21x-12x[/tex][tex]-30=9x[/tex][tex]x=\frac{-30}{9}=-\frac{10}{3}[/tex]I got the picture and will send it to you show the coordinates of the points that create the shape of the image
Answers
We have the following:
[tex]\begin{gathered} P(1-1,-3+3)\rightarrow P^{\prime}(0,0) \\ Q(3-1,-1+3)\rightarrow Q^{\prime}(2,2) \\ R(4-1,-3+3)\rightarrow R^{\prime}(3,0) \end{gathered}[/tex]now,
The answer is:
Use the remainder theorem to find P (1) for P(x) = 2x - 3x' + 3x -3.Specifically, give the quotient and the remainder for the associated division and the value of P (1).미미2Quotient = 0Х$2Remainder =0P(1) =
Answers
Using the remainder theorem, we must find P(1) for:
[tex]P(x)=2x^4-3x^3+3x-3[/tex]1) Because we want to evaluate P(x) for x = 1, we must compute
[tex]\frac{2x^4-3x^3+3x-3}{x-1}[/tex]2) Now we make the synthetic division by putting a 1 in the division box:
The remainder from the division is:
[tex]R=-1[/tex]The quotient of the division is:
[tex]2x^3-x^2+2x+2[/tex]3) From the synthetic division we get a remainder R = -1, applying the Remainder Theorem we get that:
[tex]P(1)=R=-1[/tex]Summary
The answers are:
1)
[tex]Quotient=2x^3-x^2+2x+2[/tex]2)
[tex]Remainder=-1[/tex]3)
[tex]P(1)=-1[/tex]The length of the diagonal of a Rectangle is 14cm,and it forms a 30 degree angle in one corner of the rectangle.What is the area of the rectangle.(A=LxW)
Answers
We can find W and L using the sine and the cosine functions:
[tex]\begin{gathered} \sin (30)=\frac{W}{14} \\ so\colon \\ W=14\cdot\sin (30) \\ --------- \\ \cos (30)=\frac{L}{14} \\ so\colon \\ L=14\cdot\cos (30) \end{gathered}[/tex]Therefore:
[tex]\begin{gathered} A=L\cdot W \\ A=14\cdot\cos (30)\cdot14\cdot\sin (30) \\ A=49\sqrt[]{3} \\ A\approx84.87cm^2 \end{gathered}[/tex]Answer:
84.87 cm²
Tristan tried his luck with the lottery. He can win $85 if he can correctly choose the 3 numbers drawn. If order matters and there are 13 numbers in the drawing, how many different ways could the winning numbers be drawn?
Answers
The ways to select the winning numbers is 286
How to determine the ways the winning numbers could be drawn?From the question, we have
Total numbers, n = 13Numbers to select, r = 3The winning numbers could be drawn is calculated using the following combination formula
Total = ⁿCᵣ
Where
n = 13 and r = 3
Substitute the known values in the above equation
Total = ¹³C₃
Apply the combination formula
ⁿCᵣ = n!/(n - r)!r!
So, we have
Total = 13!/10!3!
Evaluate
Total = 286
Hence, the number of ways is 286
Read more about combination at
https://brainly.com/question/11732255
#SPJ1
[tex]8.25 \div 6[/tex]8.25 divid by 6
Answers
We want to calculate the following number
[tex]\frac{8.25}{6}[/tex]To make the calcul.ation easier, we will transform the number 8.25 into a fraction. Recall that
[tex]8.25=\frac{825}{100}[/tex]So, so far, we have
[tex]\frac{8.25}{6}=\frac{\frac{825}{100}}{6}[/tex]Also, recall that
[tex]6=\frac{6}{1}[/tex]So, we have
[tex]\frac{\frac{825}{100}}{6}=\frac{\frac{825}{100}}{\frac{6}{1}}[/tex]Now, recall that when we divide fractions, we have
[tex]\frac{\frac{a}{b}}{\frac{c}{d}}=\frac{a\cdot d}{b\cdot c}[/tex]In this case, we have a=825,b=100,c=6,d=1.
So we have
[tex]undefined[/tex]question 5 only. determine the missing side length QP. the triangles are not drawn to scale.
Answers
This is a simple question.
First, we can see both triangles are proportional, it means it has the same relation between its sides even if one is in a large scale and the other on a a small scale.
Now we can identify which side corresponds to which side. Once side AC is the longest one for triangle ABC it means its equivalent for triangle PQR is the side RP, so the equivalent for side AB is side QP. Once we know that we can write the following relation and calculate:
Write the equation of a quadratic in general form, given its solutions.x=4 ; x=-1
Answers
The given solutions of the quadratic equation:
x = 4 and x = -1
First we make them factors of the equation:
x= 4 becomes:
[tex]x-4\text{ = 0}[/tex]and x = -1 becomes:
[tex]x\text{ + 1 = 0}[/tex]So (x-4) and (x+1) are the factors.
To get the general quadratic equation, we would expand the factors
[tex]\begin{gathered} (x-4)(x+1)\text{ = 0 } \\ x(x+1)\text{ -4(x+1) = 0} \\ x^2+x\text{ -4x-4 = 0} \end{gathered}[/tex][tex]\begin{gathered} Adding\text{ like terms} \\ x^2-3x-4\text{ = 0} \end{gathered}[/tex]The general quadratic equation:
[tex]x^2\text{ - 3x - 4 = 0}[/tex]Find the equation of the line passing through the points (-11,-18) and (-22,-16). Write your answer in the
form y = mx + b.
Answer: y =
Write your answers as integers or as reduced fractions in the form A/B.
Answers
Answer:
y=−2/11x−20
Step-by-step explanation:
NO LINKS!! Please help me with this probability question 2a
Answers
====================================================
Work Shown:
A = he eats pizza
B = he drinks cola
P(A) = 0.40
P(B) = 0.60
P(A and B) = 0.30
Then apply the conditional probability formula.
P(A given B) = P(A and B)/P(B)
P(A given B) = 0.30/0.60
P(A given B) = 0.5 exactly
P(A given B) = 50%
If we know for certain he drinks cola, then there's a 50% chance of him eating pizza.
Can you Help me with this i cannot do ir
Answers
To translate f(x) 4 units down we subtract 4 from f(x):
[tex]f(x)-4.[/tex]Now, to reflect f(x)-4 over the x-axis we multiply by -1:
[tex]-1(f(x)-4)=-f(x)+4.[/tex]Answer:
[tex]g(x)=-\sqrt[3]{x-2}+4.[/tex]identify the slope: 6x - 2y = -6
Answers
The slope = 3
Explanations:Note that:
The slope - Intercept form of the equation of a line takes the form y = mx + c
where m is the slope and
c is the intercept
The given equation is:
6x - 2y = -6
The equation can be re-written as:
2y = 6x + 6
2y / 2 = 6x/2 + 6/2
y = 3x + 3
The slope, m = 3
The intercept, c = 3
Y intercept=3
I need help me answering #10 I'm really bad with ratios. (also sorry for the bad lighting in the picture)
Answers
The ratio of Perch to total fish is:
3 ( Number of perch that he caught)
------------------------------------------------------
9 ( The result of the addition of all values)
Simplifying, we have:
1
---
3
So, the answer would be 1 : 3
n a recent poll, a random sample of adults in some country (18 years and older) was asked, "When you see an ad emphasizing that a product is "Made in our country," are you more likely to buy it, less likely to buy it, or neither more nor less likely to buy it?" The results of the survey, by age group, are presented in the following contingency table. Complete parts (a) through (c).
Purchase likelihood
Total
Total
Question content area bottom
Part 1
(a) What is the probability that a randomly selected individual is years of age, given the individual is to buy a product emphasized as "Made in our country"?
The probability is approximately
0.134.
(Round to three decimal places as needed.)
Part 2
(b) What is the probability that a randomly selected individual is to buy a product emphasized as "Made in our country," given the individual is years of age?
The probability is approximately
Answers
a) The probability that a randomly selected individual is 45-54 years of age, given the individual is neither more nor less likely to buy is 0.206
b) The probability that a randomly selected individual is neither more nor less likely to buy, given the individual is 45-54 years of age is 0.309
c) 18-34 year olds are less likely to buy a product emphasized as "Made in our country" than individuals in general.
Hence, the answer is no.
A random sample is one that is drawn at random from the population, meaning that every member of the population has an equal chance of being picked for the sample. The probability sampling approach is the practice of choosing people at random.
a. Total number of individuals that are neither more nor less likely to purchase = 786
Total number of individuals aged 45-54 that are neither more nor less likely to purchase = 162
The probability that a randomly selected individual is 45-54 years of age, given the individual is neither more nor less likely to buy =
= Total number of individuals aged 45-54 neither more or less likely to purchase./ Total number of individuals more or less likely to purchase.
= 162/786
= 0.206
b. Total number of individuals 45-54 years of age = 524
Total number of individuals aged 45-54 that are neither more nor less likely to purchase = 162
The probability that a randomly selected individual is neither more nor less likely to buy, given the individual is 45-54 years of age
= Total number of individuals aged 45-54 neither more or less likely to purchase./ Total number of individuals 45-54 years of age.
= 162/524
= 0.309
c. The number of 18-34 year old individuals more likely to buy = 204
The total number of 18-34 year old individuals = 523
The proportion of 18-34 year old individuals more likely to buy = 204/523
= 0.390
= 39%
The total number of individuals more likely to buy = 1266
The total number of all individuals in the survey = 2123
The proportion of individuals, in general, more likely to buy = 1266/2123
= 0.596
= 59.6%
Therefore, 18-34 year olds are less likely to buy a product emphasized as "Made in our country" than individuals in general.
Hence, the answer is no.
Learn more about Probability here:
https://brainly.com/question/24756209
#SPJ1
Your question is incomplete. Please find the missing content below.
In a recent poll, a random sample of adults in some country (18 years and older) was asked, "When you see an ad emphasizing that a product is "Made in our country," are you more likely to buy it, less likely to buy it, or neither more nor less likely to buy it?" The results of the survey, by age group, are presented in the following contingency table. Complete parts (a) through (c).
Purchase likelihood 18-34 35-44 45-54 55 and over Total
More likely 204 318 334 410 1266
Less likely 27 5 28 11 71
Neither more nor less 292 210 162 122 786
Total 523 533 524 543 2123
a) What is the probability that a randomly selected individual is 45-54 years of age, given the individual is neither more nor less likely to buy a product emphasized as "Made in our country"? The probability is approximately _____. (round to three decimal places)
b) What is the probability that a randomly selected individual is neither more nor less likely to buy a product emphasized as "Made in our country", given the individual is 45-54 years of age? The probability is approximately _____. (round to three decimal places)
c) Are 18-34-year-olds more likely to buy a product emphasized as "Made in our country" than individuals in general? Yes or no
The cost C (in dollars) of producing x units of a product is given by the following. C= 2.6. Square root of x + 600
Answers
The marginal cost in dollars of producing x units is given by the next equation:
[tex]C=2.6\sqrt[]{x}+600[/tex]a)
To find the marginal cost (in dollars per unit) when x= 9.
Then, we need to replace x=9 on the derivation of the cost equation:
So:
[tex]\frac{d}{dx}C=\frac{1.3}{\sqrt[]{x}}[/tex]Where:
[tex]\frac{d}{dx}2.6\sqrt[]{x}=2.6\frac{d}{dx}\sqrt[]{x}=2.6\frac{d}{dx}^{}x^{\frac{1}{2}}=2.6\cdot\frac{1}{2}x^{\frac{1}{2}-1}=1.3\cdot x^{-\frac{1}{2}}=\frac{1.3}{\sqrt[]{3}}[/tex]and, the derivate of a constant is equal to zero.
[tex]\frac{d}{dx}600=0[/tex]Replacing x= 9
[tex]\frac{d}{dx}C=\frac{1.3}{\sqrt[]{9}}[/tex]Hence, the marginal cost is equal to:
[tex]\frac{d}{dx}C=0.43[/tex]b) Now, when the production increases 9 to 10. It's the same as the cost of producing one more machine beyond 9.
Then, it would be x=10 on the cost equation:
[tex]C=2.6\sqrt[]{x}+600[/tex][tex]C=2.6\sqrt[]{10}+600[/tex][tex]C=608.22[/tex]and x= 9
[tex]C=2.6\sqrt[]{9}+600[/tex][tex]C=2.6(3)+600[/tex][tex]C=607.8[/tex]Then, we calculate C(10) - C(9) =
[tex]608.22-607.8[/tex][tex]=0.43[/tex]C)
Both results are equal.
Hence, the marginal cost when x=9 is equal to the additional cost when the production increases from 9 to 10.
12. A teacher weighed 148 lbs. in 1999 and weighs 190 lbs. In 2020. What was the rate ofchange in weight?
Answers
Given,
The weight of the teacher in 1999 is 148 lbs.
The weight of the teacher in 2020 is 190 lbs.
The rate of change in weight is,
[tex]\begin{gathered} \text{Rate of change=}\frac{190-148}{2020-1999} \\ =\frac{42}{21} \\ =2 \end{gathered}[/tex]The teacher gained 2 pounds per year.
Hence, option A is correct.
There are 6 dogs and 2 mice. Write a ratio for the number of ears to th number of paws. * 6:2 3 people are in a room. Write a ratio to represent the number of finger
Answers
each dog has 4 paws, then 6 dogs have 6*4 = 24 paws
each mouse has 4 paws, then 2 mice have 2*4 = 8 paws
Total number of paws: 24 + 8 = 32 paws
each dog has 2 ears, then 6 dogs have 6*2 = 12 ears
each mouse has 2 ears, then 2 mice have 2*2 = 4 ears
total number of ears: 12 + 4 = 16 ears
The ratio for the number of ears to the number of paws: 16/32 = 1/2 or 1:2
A Geiger counter counts the number of alpha particles from radioactive material. Over a
long period of time, an average of 16 particles per minute occurs. Assume the arrival of
particles at the counter follows a Poisson distribution. Round your answers to four decimals.
a) Find the probability of exactly 21 particles arrive in a particular one minute period.
0.0426053 O
b) Find the probability of exactly one particle arrives in a particular one second period.
0.20424755689724
Answers
a) The probability of exactly 21 particles arrive in a particular one minute period is 0.0426
b) The probability of exactly one particle arrives in a particular one second period is 0.2042
What is probability?Probability is the ratio of the total number of conceivable outcomes to the number of outcomes in an exhaustive set of equally likely alternatives that result in a particular occurrence.
The probability is given by:
P(X=x) = (e⁻ⁿ nˣ)/x!
a) The probability of exactly 21 particles arrive in a particular one minute period is given by :
P(X=21) = (e⁻16 × 16²¹)/21!
P(X=21) = (2.176746853×10¹⁸)/51090942171709440000
P(X=21) = 0.0426
b) The probability of exactly one particle arrives in a particular one second period is :
1 min = 16 particles
1 sec = 16/60 particles
1 sec = 0.2667 particles
P(X=1) = (e⁻⁽¹⁶/⁶⁰⁾ × (16/60)¹)/1!
P(X=1) = 0.2042
To know more about Probability please visit:
https://brainly.com/question/11234923
#SPJ13
what is 5/6 converted to decimal form
Answers
5/6 in decimal form is
[tex]\frac{5}{6}=0.8\bar{3}[/tex]Khalid is investigating two linear functions. The first linear function is defined by the equation 2x + 3y = 12. The second linear functionpasses through the points (3,-2) and (-2, k).For the case where the two linear functions have the same y-intercept, what must be the value of k?k=
Answers
According to the given data we have the following:
first linear function is defined by the equation 2x + 3y = 12
second linear function passes through the points (3,-2) and (-2, k)
the two linear functions have the same y-intercept
k?
To calculate k first we have to do the following:
we would have to use the formula y=mx +b
the two linear functions have the same y-intercept, therefore, b=12.
So, y=mx +12
As second linear function passes through the points (3,-2) we are going to substitue the x and y with 3 and -2.
So, -2=m*3+12
-2-12=m*3
-14=m*3
m=-14/3
m=-4
Finally we would calculate k by writiing the equation of the line that passes through each pair of points as follows:
y2-y1/x2-x1=m
So
[tex]\frac{k\text{ -(-2)}}{\text{-2 - 3}}\text{ }=\text{ -4}[/tex]So, k +2/-5=-4
k+2=20
k=20-2
k=18
(8-4) mulitiply (3-2)=
Answers
Solve the problem. Use 3.14 as the approximate value of pie
Answers
The volume of a cylinder is calculated using the formula:
[tex]V=\pi r^2h[/tex]where r is the radius of the cylinder and h is the height.
From the question, we have the following parameters:
[tex]\begin{gathered} diameter=4.8 \\ \therefore \\ r=\frac{4.8}{2}=2.4 \\ and \\ h=6.66 \end{gathered}[/tex]Therefore, we c n calculae tehe volume of a cylinder to be:
[tex]\begin{gathered} V=3.14\times2.4^2\times6.66 \\ V=120.455424 \end{gathered}[/tex]For four cylinders, the combined volume will be:
[tex]\begin{gathered} V=120.455424\times4 \\ V=481.821696 \end{gathered}[/tex]The volume i 481 .82 cubic inches.
a. Create a perfect square trinomial.
b. Factor the perfect square trinomial you created in 1a.
a. Create a difference of two squares.
b. Factor the difference of two squares you created in 2a.
a. Describe at least one similarity between the perfect square trinomial and the difference of squares. You can use either the form you wrote in 1a and 2a, or you can use their factored form from 1b and 2b. Write your answer using complete sentences.
b. Describe at least one difference between the perfect square trinomial and the difference of squares. You can use either the form you wrote in 1a and 2a, or you can use their factored form from 1b and 2b. Write your answer using complete sentences.
A factored perfect square might look like (x+a)(x+a) or (x-a)(x-a) [or (ax+b)(ax+b) but keep it simple]. Then, distribute.
A factored difference of two squares might look like (x+a)(x-a). Then, distribute.
(pick a number for a)
Answers
1.
a. One example of a perfect square trinomial is: x² + 6x + 9.
b. The factored trinomial above is: (x + 3)².
2.
a. One example of a difference of two squares is: x² - 4.
b. The factored difference of squares above is: (x - 2)(x + 2).
3.
a. The similarity is that the first term is positive for both cases.
b. The difference is that the final term is positive for perfect square trinomials and negative for the difference of squares.
Perfect square trinomialsThere are two examples of perfect square trinomials, the square of the sum and the square of the subtraction, as follows:
Square of the sum: (a + b)² = a² + 2ab + b².Square of the subtraction: (a - b)² = a² - 2ab + b².The left side is the factored form and the right side is the expanded form.
Hence one example of a perfect square trinomial is given as follows:
(x + 3)² = x² + 6x + 9.
Difference of two squaresA difference of two squares is factored as follows:
x² - y² = (x + 2)(x - 2)
Hence one possible example is:
x² - 4 = (x + 2)(x - 2).
Compared to the perfect square trinomial, we have that:
The similarity is that the first term in any of the two polynomials will always be positive.The difference is in the last term, for the perfect square it will always be positive (+ b²) and for the difference of two squares it will always be negative (- b²).More can be learned about perfect square trinomials at https://brainly.com/question/14584348
#SPJ1
Drag each tile to the correct box.The figures in the graph below can be shown to be similar by a sequence of transformations.Choose the correct sequence of transformations that take figure A to figure B.
Answers
Answer
Rotate 270 degrees clockwise about the origin → Translate 3 units right and 3 units up → Dilate by a scale factor of 3
Step-by-step explanation
Rotation 270 degrees clockwise about the origin transforms the point (x, y) into (-y, x). Applying this rule to the vertices of figure A, we get:
(-5, 5) → (-5, -5)
(-4, 4) → (-4, -4)
(-5, 1) → (-1, -5)
(-4, 1) → (-1, -4)
Translation 3 units right and 3 units up transform the point (x, y) into (x+3, y+3). Applying this rule to the previous points, we get:
(-5, -5) → (-5+3, -5+3) → (-2, -2)
(-4, -4) → (-4+3, -4+3) → (-1, -1)
(-1, -5) → (-1+3, -5+3) → (2, -2)
(-1, -4) → (-1+3, -4+3) → (2, -1)
Dilation by a factor of 3 transforms the point (x, y) into (3x, 3y). Applying this rule to the previous points, we get:
(-2, -2) → (3x-2, 3x-2) → (-6, -6)
(-1, -1) → (3x-1, 3x-1) → (-3, -3)
(2, -2) → (3x2, 3x-2) → (6, -6)
(2, -1) → (3x2, 3x-1) → (6, -3)
These vertices coincide with the vertices in figure B
look at the screenshots
Answers
Answer:
c for the first one and a for the second
55mL of hardener to each container of resin. How much hardener should be added to 14 containers of resin?Write your answer in liters.
Answers
The amount of hardener added to 1 container of resin = 55mL.
The amount of hardener added to 14 containers is calculated as,
[tex]\begin{gathered} \text{Amount of hardener = 55 }\times\text{ 14 } \\ \text{Amount of hardener = 770 mL} \\ \text{Amount of hardener = 0.770 L} \end{gathered}[/tex]Thus 0.770 litres of hardener must be added to 14 containers of resin.
A sector of a circle has a central angle of 60∘ . Find the area of the sector if the radius of the circle is 9 cm.
Answers
Step-by-step explanation:
area of a sector is theta ÷360 ×πr²
Note: Enter your answer and show all the steps that you use to solve this problem in the space provided
Answers
From the given picture we can see
ACB is a right triangle at C
AC = b
CB = a
AB = c
Since mSince a = 5 ft
Then to find b and c we will use the trigonometry ratios
[tex]\begin{gathered} \sin A=\frac{a}{c} \\ \sin 60=\frac{5}{c} \end{gathered}[/tex]Substitute the value of sin 60
[tex]\begin{gathered} \sin 60=\frac{\sqrt[]{3}}{2} \\ \frac{\sqrt[]{3}}{2}=\frac{5}{c} \end{gathered}[/tex]By using the cross multiplication
[tex]\begin{gathered} \sqrt[]{3}\times c=2\times5 \\ \sqrt[]{3}c=10 \end{gathered}[/tex]Divide both sides by root 3
[tex]\begin{gathered} \frac{\sqrt[]{3}c}{\sqrt[]{3}}=\frac{10}{\sqrt[]{3}} \\ c=\frac{10}{\sqrt[]{3}} \end{gathered}[/tex]To find b we will use the tan ratio
[tex]\begin{gathered} \tan 60=\frac{a}{b} \\ \tan 60=\frac{5}{b} \end{gathered}[/tex]Substitute the value of tan 60
[tex]\begin{gathered} \tan 60=\sqrt[]{3} \\ \sqrt[]{3}=\frac{5}{b} \end{gathered}[/tex]Switch b and root 3
[tex]b=\frac{5}{\sqrt[]{3}}[/tex]The exact values of b and c are
[tex]\begin{gathered} b=\frac{5}{\sqrt[]{3}} \\ c=\frac{10}{\sqrt[]{3}} \end{gathered}[/tex]What is the product of 11/12 and its reciprocal?
Answers
Answer:
The product of 11/12 is 0.916.This as as a fraction would be 0.916/1.00. This means it's reciprocal is 1.
Step-by-step explanation:
The reciprocal is basically the bottom part, denominator, of the fraction, being siwtched to on top of the fraction (numerator, and vice versa. The fraction would be 0.916/ 1.00 because the closest whole number to 0.916 is 1, meaning the fraction would be 0.916 out of 1. DO NOT MISTAKE THIS FOR 100. When you do the final step, finding the recirprocal of 0.916/1.00, we siwtch the numerator and denominators position, making out answer:
The product of 11/12 is 0.916 which is 0.916/1.00 in fraction form. The reciprocal of this is 1.00/0.916. Hope this helped!
the sales tax is 47 on the purchase of a dining room set for 940. find the sales tax rate.
Answers
The sales tax formula is used to determine how much businesses need to charge customers based on taxes in their area. State and local governments across the United States use a sales tax to pay for things like roads, healthcare and other government services. Sales tax applies to most consumer product purchases and exists in most states.
The sales tax formula is simply the sales tax percentage multiplied by the price of the item. It's important for businesses to know how to use the sales tax formula so that they can charge their customers the proper amount to cover the tax. For consumers, it's good to know how the sales tax formula works so that you can properly budget for your purchases
The sales tax formula is as shown below:
[tex]\text{sales tax=sales tax percentage }\times Price\text{ of the items}[/tex]Given that
Sales tax = 47
price of the dining room = 940
Sales tax rate= unknown
To find the sales tax rate, we would substitute into the formula above
[tex]\begin{gathered} 47=\text{sales tax rate }\times940 \\ \text{sales tax rate = }\frac{47}{940}\times100\text{ \%} \\ \text{sales tax rate = }\frac{1}{20}\times100=0.05\times100\text{ \%} \\ \text{sales tax rate= 5 \%} \end{gathered}[/tex]Hence, the sales tax rate is 5%