Answers
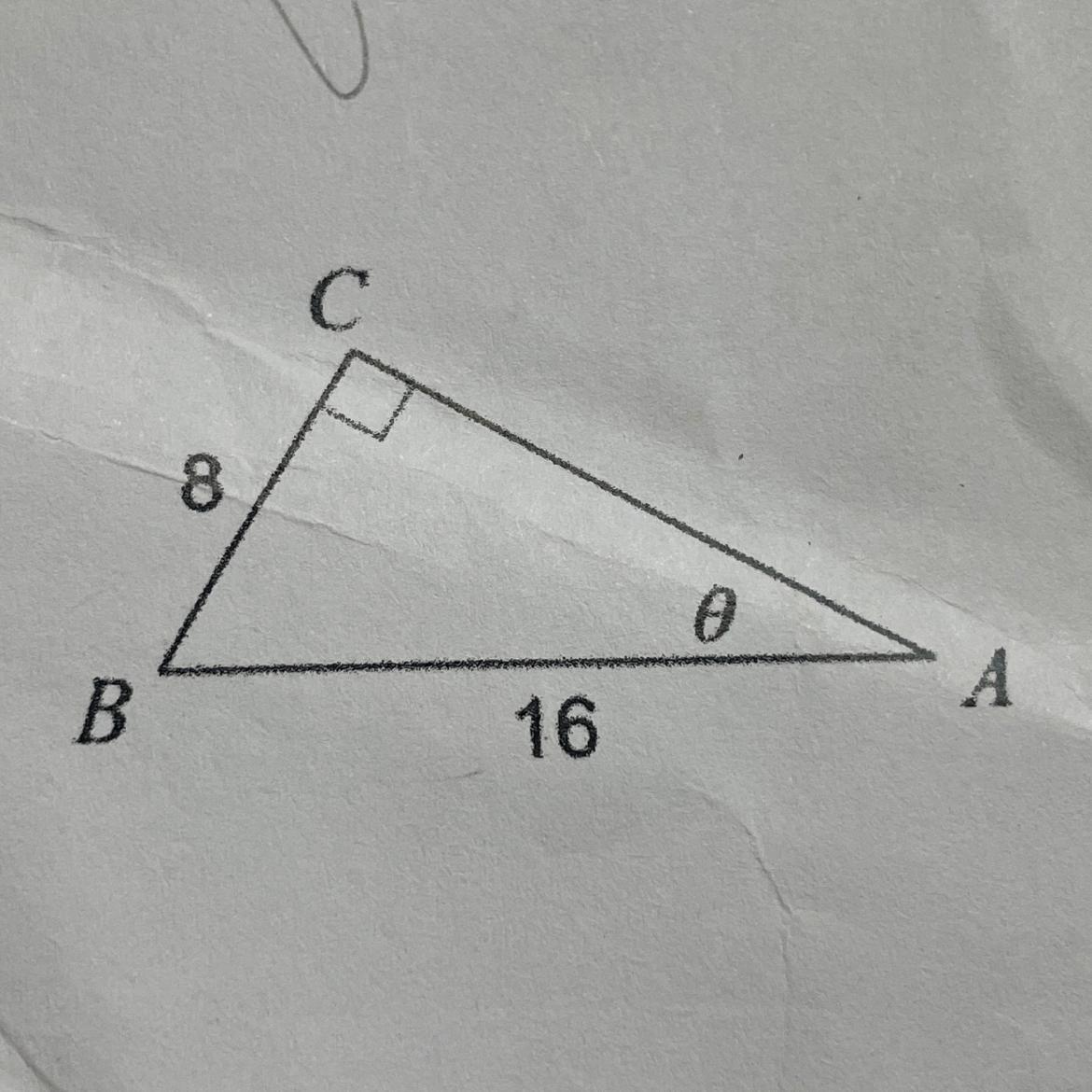
The measure of angle A and angle B are 30° and 60° respectively.
What is the measure of angle A and angle B?The figure in the image is a right-triangle.
To find the measure of angle A and angle B, we use the trigonometric ratio.
Solving for the measure of angle A:
sinθ = opposite / hypotenuse
opposite of angle A = 8
hypotenuse = 16
Plug in the values
sinθ = 8/16
sinθ = 1/2
θ = sin⁻¹( 1/2 )
θ = 30°
Solving for angle B
cosB = adjacent / Hypotenuse
adjeacent of angle B = 8
Hypotenuse = 16
Plug in the given values
cosB = 8/16
cosB = 1/2
B = cos⁻¹( 1/2 )
B = 60°
Therefore angle A is 30 degrees and angle B is 60 degree.
Learn more about trigonometric ratio here: brainly.com/question/28016662
#SPJ1
Related Questions
Your cousin bought a used car. He paid a total of $12,755 for the car. The total cost includes: • The list price of the car, x • A 7% sales tax on the list price . Plus $450 in additional fees.
What is the price of the car your cousin bought?
List price:
Answers
Let's use the variable x to represent the list price of the car.
The total cost your cousin paid for the car is the list price plus a 7% sales tax on the list price, plus $450 in additional fees.
We can write this as an equation:
Total cost = List price + 0.07(List price) + 450
We know that the total cost your cousin paid was $12,755, so we can substitute that into the equation:
12,755 = x + 0.07x + 450
Simplifying the right side:
12,755 = 1.07x + 450
Subtracting 450 from both sides:
12,305 = 1.07x
Dividing both sides by 1.07:
x = 11,500
Therefore, the list price of the car your cousin bought was $11,500.
The list price of the car your cousin bought was $11,500.
What is an expression?An expression contains one or more terms with addition, subtraction, multiplication, and division.
We always combine the like terms in an expression when we simplify.
We also keep all the like terms on one side of the expression if we are dealing with two sides of an expression.
Example:
1 + 3x + 4y = 7 is an expression.com
3 + 4 is an expression.
2 x 4 + 6 x 7 – 9 is an expression.
33 + 77 – 88 is an expression.
We have,
Let's start by setting up an equation to represent the total cost of the car:
Total cost = List price + 7% of List price + $450
We know that the total cost is $12,755, so we can substitute that in:
$12,755 = List price + 0.07(List price) + $450
Simplifying this equation, we get:
$12,755 = 1.07(List price) + $450
Subtracting $450 from both sides, we get:
$12,305 = 1.07(List price)
Dividing both sides by 1.07, we get:
List price = $11,500
Therefore,
The list price of the car your cousin bought was $11,500.
Learn more about expressions here:
https://brainly.com/question/3118662
#SPJ2
John buys new baseball equipment for $2000. The purchase made is with a credit card that has a 19% APR. John makes a $150 payment monthly. How many months will it take John to pay off the balance?
Answers
It will take John approximately 17 months to pay off the balance.
What is simple interest?
Simple Interest (S.I.) is the method of calculating the interest amount for a particular principal amount of money at some rate of interest.
Assuming that John does not use the credit card for any other purchases and that the credit card company uses a simple interest calculation method, we can use the following steps to calculate the number of months it will take John to pay off the balance:
Calculate the monthly interest rate by dividing the annual percentage rate (APR) by 12:
Monthly interest rate = 19% / 12 = 0.01583
Calculate the monthly finance charge by multiplying the outstanding balance by the monthly interest rate:
Monthly finance charge = $2000 x 0.01583 = $31.66
Subtract the monthly payment from the monthly finance charge to get the amount that will be applied to the outstanding balance:
Payment applied to balance = $150 - $31.66 = $118.34
Divide the outstanding balance by the payment applied to balance to get the number of months it will take to pay off the balance:
Number of months to pay off balance = $2000 / $118.34 = 16.9
(rounded up to the nearest whole number)
Therefore, it will take John approximately 17 months to pay off the balance.
To learn more about the simple interest visit:
brainly.com/question/20690803
#SPJ1
do less republicans (group a) than democrats (group b) favor the government investing billions of dollars to improve the country's train system? one thousand republicans and one thousand democrats were asked if they favored spending billions to improve the country's train system. how would we write the alternative hypothesis?
Answers
The alternative hypothesis can be written as H₁: pA < pB.
The alternative hypothesis would be that there is a difference in the proportion of Republicans (Group A) and Democrats (Group B) who favor the government investing billions of dollars to improve the country's train system. Expressly, it would state that the proportion of Republicans who favor this investment is less than the proportion of Democrats who favor it:
H₁: pA < pB
where pA denotes the proportion of Republicans who favor the investment and pB denotes the proportion of Democrats who favor the investment.
In the alternative hypothesis, we actually create the relationship between the variables which are being tested in that situation. According to these, we come across the comparison among the variables and how much they differ from each other. The alternative hypothesis is the statement the researcher tries to prove by conducting a statistical analysis.
Learn more about alternative hypothesis;
https://brainly.com/question/26185548
#SPJ4
Let s be the set of all orderd pairs of real numbers. Define scalar multiplication and addition on s by
Answers
In the 8 Axioms, 4 and 6 axioms fails to holds and S is not a vector space. Rest of the axioms try to hold the vector space.
To demonstrate that S is not a vector space, we must demonstrate that at least one of the eight vector space axioms fails to hold. Let us examine each axiom in turn:
Closure under addition: For any (x₁, x₂) and (y₁, y₂) in S, their sum (x₁ + y₁, 0) is also in S. This axiom holds.Commutativity of addition: For any (x₁, x₂) and (y₁, y₂) in S, (x₁ + y₁, 0) = (y₁ + x₁, 0). This axiom holds.Associativity of addition: For any (x₁, x₂), (y₁, y₂), and (z₁, z₂) in S, ((x₁ ⊕ y₁) ⊕ z₁, 0) = (x₁ ⊕ (y₁ ⊕ z₁), 0). This axiom holds.The Identity element of addition: There exists an element (0, 0) in S such that for any (x₁, x₂) in S, (x₁, x₂) ⊕ (0, 0) = (x₁, x₂). This axiom fails because (x₁, x₂) ⊕ (0, 0) = (x₁, 0) ≠ (x₁, x₂) unless x₂ = 0.Closure under scalar multiplication: For any α in the field of real numbers and (x₁, x₂) in S, α(x₁, x₂) = (αx₁, αx₂) is also in S. This axiom holds.Inverse elements of addition: For any (x₁, x₂) in S, there exists an element (-x₁, 0) in S such that (x₁, x₂) ⊕ (-x₁, 0) = (0, 0). This axiom fails because (-x₁, 0) is not well-defined as the inverse of (x₁, x₂) because (x₁, x₂) ⊕ (-x₁, 0) = (0, 0) holds only if x₂=0.Distributivity of scalar multiplication over vector addition: For any α in the field of real numbers and (x₁, x₂), (y₁, y₂) in S, α ((x₁, x₂) ⊕ (y₁, y₂)) = α(x₁ + y₁, 0) = (αx₁ + αy₁, 0) = α(x₁, x₂) ⊕ α(y₁, y₂). This axiom holds.Distributivity of scalar multiplication over field addition: For any α, β in the field of real numbers and (x₁, x₂) in S, (α + β) (x₁, x₂) = ((α + β)x₁, (α + β)x₂) = (αx₁ + βx₁, αx₂ + βx₂) = α(x₁, x₂) ⊕ β(x₁, x₂). This axiom holds.Therefore, axioms 4 and 6 fail to hold, and S is not a vector space.
Learn more about Scalar Multiplication:
https://brainly.com/question/28890483
#SPJ4
The correct question:
Let S be the set of all ordered pairs of real numbers. Define scalar multiplication and addition on S by α(x₁, x₂) = (αx₁, αx₂); (x₁, x₂) ⊕ (y₁, y₂) = (x₁ + y₁, 0). We use the symbol ⊕ to denote the addition operation for this system in order to avoid confusion with the usual addition x + y of row vectors. Show that S, together with the ordinary scalar multiplication and the addition operation ⊕, is not a vector space. Which of the eight axioms fail to hold?
SALES An automobile company sold 2.3 million new cars in a year. If the average price per car was $21,000, how
much money did the company make that year? Write your answer in scientific notation.
Answers
Therefore, the company made $48.3 million (written in scientific notation as 4.83 x 10⁷) that year from selling new cars.
What is equation?An equation is a mathematical statement that shows that two expressions are equal. It consists of two sides, the left-hand side (LHS) and the right-hand side (RHS), separated by an equals sign (=). The expressions on both sides of the equals sign must have the same value for the equation to be true. Equations can involve a wide range of mathematical operations such as addition, subtraction, multiplication, division, exponents, and roots. They are used to solve problems in various fields such as physics, engineering, economics, and many others.
Here,
To find the total revenue generated by the company, we need to multiply the number of new cars sold by the average price per car. We can do this as follows:
Total revenue = number of new cars sold x average price per car
Total revenue = 2.3 million x $21,000
To multiply these two numbers, we can use the distributive property:
Total revenue = (2.3 x 10⁶) x ($21,000)
Total revenue = 2.3 x $21 x 10⁶
Multiplying 2.3 by 21 gives us 48.3, which we can write in scientific notation as 4.83 x 10¹. We can then add the exponents to get:
Total revenue = 4.83 x 10¹ x 10⁶
Total revenue = 4.83 x 10⁷
To know more about equation,
https://brainly.com/question/28243079
#SPJ1
Using Trig to find a side.
Solve for x. Round to the nearest tenth, if necessary.
Answers
Answer:
[tex]\large\boxed{\tt x \approx 95.6}[/tex]
Step-by-step explanation:
[tex]\textsf{We are asked to solve for x by using \underline{Trigonometric Identities}.}[/tex]
[tex]\large\underline{\textsf{What are Trigonometric Identities?}}[/tex]
[tex]\boxed{\begin{minipage}{20 em} \\ \underline{\textsf{\large Trigonometric Identities;}} \\ \\ \textsf{Trigonometric Identities are trigonometric ratios determined with what's given in order to find a missing value. For a Right Triangle, the Trigonometric Identities are Sine, Cosine, and Tangent. These are used to find missing sides.} \\ \\ \tt Sine = \tt $ \tt \frac{Opposite}{Hypotenuse} \\ \\ Cosine = \frac{Adjacent}{Hypotenuse} \\ \\ Tangent = \frac{Opposite}{Adjacent} \end{minipage}}[/tex]
[tex]\textsf{We should determine whether Sine, Cosine, or Tangent will actually help us}[/tex]
[tex]\textsf{determine x. We are given a Right Triangle that has 1 15}^{\circ} \ \textsf{angle, and a side with}[/tex]
[tex]\textsf{a length of 99. Because this side is opposite of the right angle, this side is called}[/tex]
[tex]\textsf{the \underline{Hypotenuse}.}[/tex]
[tex]\textsf{The side labeled x is \underline{Adjacent}, which means that it's touching the given angle.}[/tex]
[tex]\textsf{Using what was given to us, we should use Cosine since we are asked for the}[/tex]
[tex]\textsf{Adjacent Angle when given the Hypotenuse.}[/tex]
[tex]\large\underline{\textsf{Solving;}}[/tex]
[tex]\textsf{Remember that;}[/tex]
[tex]\tt \cos(15^{\circ}) =\frac{Adjacent}{Hypotenuse}[/tex]
[tex]\textsf{We're given;}[/tex]
[tex]\tt \cos(15^{\circ}) =\frac{x}{99}[/tex]
[tex]\textsf{To find the value of x, we first should remove the fraction using cancellation.}[/tex]
[tex]\textsf{We are able to use the \underline{Multiplication Property of Equality} to prove that the}[/tex]
[tex]\textsf{equation remains equal.}[/tex]
[tex]\underline{\textsf{Multiply both expressions by 99;}}[/tex]
[tex]\tt 99 \cos(15^{\circ}) =\not{99} \frac{x}{\not{99}}[/tex]
[tex]\tt 99 \cos(15^{\circ}) =x[/tex]
[tex]\underline{\textsf{Evaluate;}}[/tex]
[tex]\tt 99 \cos(15^{\circ}) \approx \boxed{\tt 95.6}[/tex]
[tex]\large\boxed{\tt x \approx 95.6}[/tex]
in general, if sample data are such that the null hypothesis is rejected at the a 5 1% level of significance based on a two-tailed test, is h0 also rejected at the a 5 1% level of significance for a corresponding onetailed test? explain.
Answers
The directionality of the alternative hypothesis and the support offered by the sample data determine whether the null hypothesis is likewise rejected at the 5% level of significance for a related one-tailed test.
When the two-tailed test rejects the null hypothesis, it means that the sample data, regardless of how we look at it, support the null hypothesis.. A one-tailed test, however, simply considers the evidence in one way. As a result, the null hypothesis should be used if the sample data only show evidence that the alternative hypothesis is true in one direction (for example, greater than).
To know more about Null hypothesis, visit,
https://brainly.com/question/4436370
#SPJ4
1. Find the square root of each of the following numbers: (i) 152.7696
Answers
1. Start by making pairs of digits from the right: 15, 27, 69, 6.
2. Find the largest integer whose square is less than or equal to the first pair, which is 15. Since 3^2 = 9 < 15 and 4^2 = 16 > 15, the integer we are looking for is 3.
3. Write the digit 3 as the first digit of the square root.
4. Subtract the square of 3 from 15 to get 6.
5. Bring down the next pair of digits, 27, and append them to 6 to get 627.
6. Double the first digit of the current root estimate (which is 3) to get 6.
7. Find the largest digit to fill in the blank in "3_ × _ = 6" such that the resulting product is less than or equal to 627. This digit is 7, since 3×7 = 21 < 627 and 3×8 = 24 > 627.
8. Write down the digit 7 as the second digit of the root estimate.
9. Subtract the square of 37 from 627 to get 60.
10. Bring down the next pair of digits, 69, and append them to 60 to get 6069.
11. Double the first digit of the current root estimate (which is 37) to get 74.
12. Find the largest digit to fill in the blank in "37_ × _ = 606" such that the resulting product is less than or equal to 6069. This digit is 1, since 37×1 = 37 < 6069 and 37×2 = 74 > 6069.
13. Write down the digit 1 as the third digit of the root estimate.
14. Subtract the square of 371 from 6069 to get 152.769.
Therefore, the square root of 152.7696 is approximately 12.36 (rounded to two decimal places).
brainlist
show all steps nd i will make u brainlist
Answers
Step-by-step explanation:
Again, using similar triangle ratios
7.2 m is to 2.4 m
as AB is to 12.0 m
7.2 / 2.4 = AB/12.0 Multiply both sides of the equation by 12
12 * 7.2 / 2.4 = AB = 36.0 meters
Suppose that $18,000 is invested at 5. 2% compounded. Find the total amount of this investment after 7 years
Answers
If $18,000 is invested at 5. 2% compounded then the full sum of the investment after 7 long years is roughly $24,810.89.
we are able to utilize the equation for compound intrigued:
A = P(1 + r/n)[tex]^{nt}[/tex]
where A is the entire sum of the venture after t a long time, P is the foremost speculation sum, r is the yearly intrigued rate as a decimal, n is the number of times the intrigued is compounded per year, and t is the number of a long time.
In this case, P = $18,000, r = 0.052 (since the intrigued rate is 5.2%), n = 1 (since the intrigued is compounded every year), and t = 7 (since we need to discover the full sum after 7 a long time). Substituting these values into the equation, we get: A = 18000(1 + 0.052/1)[tex]^{1*7}[/tex]
= 18000(1.052)[tex]^{7}[/tex]
= $24,810.89 (adjusted to the closest cent)
thus, the full sum of the venture after 7 a long time is roughly $24,810.89.
To learn about investment visit:
https://brainly.com/question/15105766
#SPJ4
Habib drew a new diagram that has an area of [tex]6+4s^2[/tex].
What is the area of Habib's diagram when [tex]s=1/2[/tex]?
Answers
The area of Habib's diagram when s = 1/2 is 7.
What is circle?
A circle is a geometric shape that consists of all points in a plane that are equidistant from a fixed point called the center. It can also be defined as the set of points that are a fixed distance (called the radius) away from the center point. The distance around the circle is called its circumference, and the distance across the circle passing through the center is called its diameter.
To find the area of Habib's diagram when s = 1/2, we just need to substitute s = 1/2 into the expression for the area:
Area = 6 + 4s²
Area = 6 + 4(1/2)²
Area = 6 + 4(1/4)
Area = 6 + 1
Area = 7
Therefore, the area of Habib's diagram when s = 1/2 is 7.
To learn more about circle from the given link:
https://brainly.com/question/29142813
#SPJ1
Find the length of the side labeled x. Explain.
Answers
The value of the length marked x is 61.5
What is trigonometrical ratio?Trigonometric ratios in trigonometry relate the ratio of sides of a right triangle to the respective angle. The basic trigonometric ratios are sine, cosine, and tangent ratios. The other important trig ratios, cosec, sec, and cot can be derived using the sin, cos and tan respectively.
First using left hand side
Cos = Adj/Hypo
Cos22 = Adj/50
Adj = 50 * Cos 22
The adj = 50*0.9272
The adj = 46.4
The to find x, using
Cos 41 = 46.4/x
xCos41 =46.4
x = 46.4/Cos41
x = 46.4/.0755
Therefore the value of x = 61.5
Learn more about trigonometrical ratios on https://brainly.com/question/25122825
#SPJ1
solve -3(x-3)≤ 5(1-x)
Answers
-3x+9<5-5x
The collect the like terms
-3x+5x<5-9
The compute the numbers
2x<-4
The cancel to 2 by 2 to make x only
2x<-4
—- —
2 2
And finally you will find the answer
X=-2
When Ranim started karate, her highest kick went
11
0
∘
110
∘
110, degrees from the ground. Her instructor asked her to practice until her highest kick goes
15
5
∘
155
∘
155, degrees from the ground. Which equation will tell us the measure of the additional angle,
a
aa, that Ranim's kick needs to go to reach
15
5
∘
155
∘
155, degrees from the ground?
Choose 1 answer:
Answers
The equation that will tell us measure of additional angle, a, that Ranim's kick needs to go to reach 155 degrees from the ground is given option 155 - 110 = a.
Highest kick went when Ranim started karate from the ground is
= 110 degrees
Highest kick limit given by instructor from the ground = 155 degrees
This equation represents the difference between the final desired angle of 155 degrees and the initial angle of 110 degrees.
Which Ranim's kick went when she started karate.
The result of this subtraction will give us the measure of the additional angle, a.
That Ranim needs to add to her kick to reach the new desired angle.
Therefore, equation representing the measure of the additional angle a, of Ranim karate kick is equal to 155 - 110 = a.
Learn more about measure here
brainly.com/question/16482000
#SPJ4
The above question is incomplete, the complete question is:
When Ranim started karate, her highest kick went 110 degrees from the ground. Her instructor asked her to practice until her highest kick goes 155 degrees from the ground. Which equation will tell us the measure of the additional angle, a, that Ranim's kick needs to go to reach 155 degrees from the ground?
155−110=a
155+110=a
180−110=a
155+90=a
5(2x - 1) + 3(x - 3) = -(4x - 6) + 2(13 - 3x)
Answers
Answer:
The value of x is 2.
Step-by-step explanation:
5(2x -1) + 3(x -3) = -(4x - 6) + 2(13 -3x)
Expand both sides of the equation to remove parenthesis
10x - 5 + 3x - 9 = -4x + 6 + 26 - 6x
Transpose all terms with x as the coefficient on the left side of the equation and transpose the constants to the right.
10x + 3x + 4x + 6x = 6 + 26 + 5 + 9
Simplify
23x = 46
Divide both sides of the equation by 23
23x/23 = 46/23
x = 2
suppose the customers arrive at a starbucks shop at an average rate of 1/min. use a poisson process to model the arrival of customers. what is the probability that at least one customer arrives at the shop during a one-minute interval? 0.736 0.368 0.632 0.264
Answers
The probability that at least one customer arrives at the shop during a one-minute interval is 0.632.
Since the arrival of customers at a Starbucks shop can be modeled as a Poisson process with an average rate of 1/min, the probability of exactly k customers arriving in a one-minute interval is given by the Poisson probability mass function:
P(k arrivals) = (λ^k * e^(-λ)) / k!
where λ is the average rate of arrivals (in this case, 1/min), e is the mathematical constant e, and k! is the factorial of k.
To find the probability that at least one customer arrives during a one-minute interval, we can use the complement of the probability that zero customers arrive (i.e., the probability of at least one arrival is 1 minus the probability of zero arrivals).
Thus, the probability of at least one customer arriving during a one-minute interval is:
P(at least one arrival) = 1 - P(0 arrivals)
P(at least one arrival) = 1 - [([tex]1^{0}[/tex] * [tex]e^{-1}[/tex]) / 0!] = 1 - [tex]e^{-1}[/tex] = 0.632
Therefore, the probability that at least one customer arrives at the shop during a one-minute interval is 0.632.
Learn more about Poission;
https://brainly.com/question/30992240
#SPJ4
what is the 4th term/number of (a+b)^9, pascal’s triangle?
Answers
Step-by-step explanation:
hope this will help you Thanks
Helppp on this problem
Answers
The missing angles of the diagram are:
∠1 = 118°
∠2 = 62°
∠3 = 118°
∠4 = 30°
∠5 = 32°
∠6 = 118°
∠7 = 30°
∠8 = 118°
How to find the missing angles?Supplementary angles are defined as two angles that sum up to 180 degrees. Thus:
∠1 + 62° = 180°
∠1 = 180 - 62
∠1 = 118°
Now, opposite angles are congruent and ∠2 is an opposite angle to 62°. Thus: ∠2 = 62°.
Similarly: ∠3 = 118° because it is congruent to ∠1
Alternate angles are congruent and ∠5 is an alternate angle to 32°. Thus:
∠5 = 32°
Sum of angle 4 and 5 is a corresponding angle to ∠2 . Thus:
∠4 + ∠5 = 62
∠4 + 32 = 62
∠4 = 30°
This is an alternate angle to ∠7 and as such ∠7 = 30°
Sum of angles on a straight line is 180 degrees and as such:
∠8 = 180 - (30 + 32)
∠8 = 118° = ∠6 because they are alternate angles
Read more about Missing Angles at: https://brainly.com/question/28293784
#SPJ1
there are 90 people in the restaurant. the probability of someone ordering a drink with the food is 60%. use normal approximation of binomial distribution to answer the following 6 questions. 1. what is the mean of the normal distribution? 2. what is the standard deviation of the normal distribution? 3. what is the probability that exactly 50 people will order a drink? 4. what the probability that more than 50 people will order a drink? 5. what is the probability that less than 50 people will order a drink? 6. what is the probability that between 52 or more and 56 or less people will order a drink?
Answers
1. Mean = 54
2. Standard Deviation = 6.3
3. Probability = 0.077
4. Probability = 0.845
5. Probability = 0.155
6. Probability = 0.323
Find all of the cube roots of 216i and write the answers in rectangular (standard) form.
Answers
The cube roots of 216 written in the rectangular (standard) form are 3 + 3√3, -3+3√3, and 6.
What is a cube root?In mathematics, the cube root formula is used to represent any number as its cube root, for example, any number x will have the cube root 3x = x1/3. For instance, 5 is the cube root of 125 as 5 5 5 equals 125.
3√216 = 3√(2x2x2)x(3x3x3)
= 2 x 3 = 6
the prime factors are represented as cubes by grouping them into pairs of three. As a result, the necessary number, which is 216's cube root, is 6.
Therefore, the cube roots of 216 are 3 + 3√3, -3+3√3, and 6.
Learn more about cube root, here:
https://brainly.com/question/31153573
#SPJ1
Callie owns a business and wants to know if the majority of her customers are satisfied. She surveys a random sample of 25 customers, and 17 customers report being satisfied. In a second random sample of 25 customers, 12 customers report being satisfied. The results of the third and fourth surveys of random samples of 25 customers finds 14 and 9 satisfied customers, respectively. Which statement BEST describes the sample mean absolute deviation for this data set?
Answers
Therefore, the statement "The sample mean absolute deviation is likely to be higher for the samples with lower satisfaction rates" would be the BEST description of the MAD for this data set.
To calculate the mean absolute deviation (MAD), we first need to find the mean of each sample.
Sample 1:[tex]17/25 = 0.68[/tex]
Sample 2: [tex]12/25 = 0.48[/tex]
Sample 3: [tex]14/25 = 0.56[/tex]
Sample 4: [tex]9/25 = 0.36[/tex]
Next, we calculate the deviation of each observation from its respective sample mean:
Sample 1: |0.68 - x1|, |0.68 - x2|, ..., |0.68 - x25|
Sample 2: |0.48 - x1|, |0.48 - x2|, ..., |0.48 - x25|
Sample 3: |0.56 - x1|, |0.56 - x2|, ..., |0.56 - x25|
Sample 4: |0.36 - x1|, |0.36 - x2|, ..., |0.36 - x25|
where xi is the satisfaction rating (0 or 1) of the Ith customer in the sample.
The MAD is the average of these deviations:
MAD = (|0.68 - x1| + |0.68 - x2| + ... + |0.36 - x25|)/100
Since we don't know the actual ratings of the customers, we cannot calculate the MAD exactly. However, we can say that the MAD is likely to be higher for samples 2 and 4, which have lower satisfaction rates, compared to samples 1 and 3, which have higher satisfaction rates. Therefore, the statement "The sample mean absolute deviation is likely to be higher for the samples with lower satisfaction rates" would be the BEST description of the MAD for this data set.
To know more about average visit:
https://brainly.com/question/27646993
#SPJ1
Jose is wrapping a stack of 100 coins in a paper holder. Each coin is 18
inch thick and has a diameter of
1 inch. How many square inches of paper will Jose need to cover the stack of coins?
Answers
Jose needs 61.23 square inches of paper to cover the stack of coins.
How many square inches of paper will Jose need to cover the stack of coins?The total thickness of the stack of 100 coins is 100 x 0.18 = 18 inches. The diameter of each coin is 1 inch, so the radius of each coin is 0.5 inches.
To find the amount of paper needed to cover the stack of coins, we need to calculate the total surface area of the stack.
The area of each circle is given by:
πr^2 where r is the radius of the coin.
The area of the top and bottom circles is:
2 x π x (0.5)^2 = 0.5π
The circumference of the circle is given by:
2πr
So, the circumference of each coin is:
2π(0.5) = π
The height of the stack is 18 inches, so the area of the curved surface is:
π x 18 = 18π
Therefore, the total surface area of the stack is:
1.5π + 18π = 19.5π
To cover the stack of coins with paper, Jose will need 19.5π square inches of paper.
19.5π ≈ 19.5 x 3.14 ≈ 61.23 square inches.
Therefore, Jose will need approximately 61.23 square inches of paper to cover the stack of coins.
Read more about area at
https://brainly.com/question/24487155
#SPJ1
Find the missing side.
Answers
The measure of the unknown side from the given triangle is 14.48.
Solving trigonometry identityThe given triangle is a right triangle with the following sides;
Hypotenuse = 15
Adjacent = x
Acute angle = 52 degrees
We are to determine the measure of the unknown side using trigonometry identity
Cos 15 = Adjacent/Hypotenuse
Cos 15 = x/15
x = 15cos15
x = 15(0.9659)
x = 14.48
Hence the measure of the unknown side is 14.48
Learn more on trigonometry identity here: https://brainly.com/question/24496175
#SPJ1
Given C(2, −8), D(−6, 4), E(0, 4), U(1, −4), V(−3, 2), and W(0, 2), and that △CDE is the preimage of △UVW, represent the transformation algebraically.
Answers
Rotate triangle △C'D'E' counterclockwise by approximately -0.785 radians about the origin:
[tex]x1' = 1 \times cos(-0.785) - (-4) \times sin(-0.785) \approx 0.436[/tex]
[tex]y1' = 1 \times sin(-0.785) + (-4) \times cos(-0.785) \approx -3.678[/tex]
[tex]x2' = -7 \times cos(-0.785) - 8[/tex]
What is the coordinate of the point?The given point [tex]s C(2, -8), D(-6, 4),[/tex] and [tex]E(0, 4)[/tex] form the triangle △CDE, and the points U(1, -4), V(-3, 2), and W(0, 2) form the triangle △UVW, with △CDE being the preimage of △UVW.
To represent the transformation algebraically, we can use a combination of translations and rotations.
Translation:
To translate a point (x, y) by a vector (h, k), we add h to the x-coordinate and k to the y-coordinate of the point.
To transform triangle △CDE to triangle △UVW, we can first translate triangle △CDE by a vector (h, k) to obtain triangle △C'D'E', where C' = C + (h, k), D' = D + (h, k), and E' = E + (h, k).
Since the coordinates of C are (2, -8) and the coordinates of U are (1, -4), we can calculate the translation vector (h, k) as follows:
[tex]h = 1 - 2 = -1[/tex]
[tex]k = -4 - (-8) = 4[/tex]
So the translation vector is [tex](-1, 4).[/tex]
Rotation:
To rotate a point (x, y) by an angle θ counterclockwise about the origin, we use the following formulas:
[tex]x' = x \times \cos(\theta) - y times \sin(\theta)[/tex]
[tex]y' = x \times \sin(\theta) + y \times \cos(\theta)[/tex]
To transform triangle △C'D'E' to triangle △UVW, we can apply a rotation of angle θ counterclockwise about the origin to triangle △C'D'E', where C' = (x1', y1'), D' = (x2', y2'), and E' = (x3', y3'). Since the coordinates of C' are (2, -8) after translation, and the coordinates of U are (1, -4), we can calculate the rotation angle θ as follows:
[tex]\theta = atan2(y1' - y2', x1' - x2') - atan2(y1 - y2, x1 - x2)= atan2((-8 + 4) - (-4), (2 + 1) - (-6 + 3)) - atan2((-8) - (-4), 2 - (-6))[/tex]
Using a calculator, we can find θ to be approximately -0.785 radians.
So, the algebraic representation of the transformation that maps triangle [tex]\triangle CDE[/tex] to triangle [tex]\triangle UVW[/tex] is:
Translate triangle △CDE by the vector (-1, 4) to obtain triangle △C'D'E':
[tex]C' = (2, -8) + (-1, 4) = (1, -4)[/tex]
[tex]D' = (-6, 4) + (-1, 4) = (-7, 8)[/tex]
[tex]E' = (0, 4) + (-1, 4) = (-1, 8)[/tex]
Therefore, Rotate triangle △C'D'E' counterclockwise by approximately -0.785 radians about the origin:
[tex]x1' = 1 \times cos(-0.785) - (-4) \times sin(-0.785) \approx 0.436[/tex]
[tex]y1' = 1 \times sin(-0.785) + (-4) \times cos(-0.785) \approx -3.678[/tex]
[tex]x2' = -7 \times cos(-0.785) - 8[/tex]
Learn more about coordinate here:
https://brainly.com/question/16634867
#SPJ1
Decide if the following situation is a permutation or combination and solve. A coach needs five starters from the team of 12 players. How many different choices are there?
Answers
Answer: This situation involves choosing a group of 5 players out of a total of 12 players, where the order in which the players are chosen does not matter. Therefore, this is an example of a combination problem.
The number of ways to choose a group of 5 players out of 12 is given by the formula for combinations:
n C r = n! / (r! * (n-r)!)
where n is the total number of players, r is the number of players being chosen, and "!" represents the factorial operation.
In this case, we have n = 12 and r = 5, so the number of different choices of starters is:
12 C 5 = 12! / (5! * (12-5)!)
= 792
Therefore, there are 792 different choices of starters that the coach can make from the team of 12 players.
Step-by-step explanation:
a blanket measures 1 1/4 yards on each side. how many square yards does the blanket cover?
Answers
Answer:
Add 1 1/4 x 1 1/4
Step-by-step explanation:
hat is the maximum speed of a point on the outside of the wheel, 15 cm from the axle?
Answers
It depends on the rotational speed of the wheel. To calculate this speed, we need to know the angular velocity of the wheel.
The maximum speed of a point on the outside of the wheel, 15 cm from the axle, if we assume that the wheel is rotating at a constant rate, we can use the formula v = rω, where v is the speed of the point on the outside of the wheel, r is the radius of the wheel (15 cm in this case), and ω is the angular velocity of the wheel. Therefore, the maximum speed of a point on the outside of the wheel would be directly proportional to the angular velocity of the wheel.
The formula to calculate the maximum linear speed (v) is:
v = ω × r
where v is the linear speed, ω is the angular velocity in radians per second, and r is the distance from the axle (15 cm, or 0.15 meters in this case).
Once you have the angular velocity (ω) of the wheel, you can plug it into the formula and find the maximum speed of a point on the outside of the wheel.
Learn more about rotational speed here: brainly.com/question/17025846
#SPJ11
if x is a matrix of centered data with a column for each field in the data and a row for each sample, how can we use matrix operations to compute the covariance matrix of the variables in the data, up to a scalar multiple?
Answers
To compute the covariance matrix of the variables in the data, the "matrix-operation" which should be used is ([tex]X^{t}[/tex] × X)/n.
The "Covariance" matrix is defined as a symmetric and positive semi-definite, with the entries representing the covariance between pairs of variables in the data.
The "diagonal-entries" represent the variances of individual variables, and the off-diagonal entries represent the covariances between pairs of variables.
Step(1) : Compute the transpose of the centered data matrix X, denoted as [tex]X^{t}[/tex]. The "transpose" of a matrix is found by inter-changing its rows and columns.
Step(2) : Compute the "dot-product" of [tex]X^{t}[/tex] with itself, denoted as [tex]X^{t}[/tex] × X.
The dot product of two matrices is computed by multiplying corresponding entries of the matrices and summing them up.
Step(3) : Divide the result obtained in step(2) by the number of samples in the data, denoted as "n", to get the covariance matrix.
This step scales the sum of the products by 1/n, which is equivalent to taking the average.
So, the covariance matrix "C" of variables in "centered-data" matrix X can be expressed as: C = ([tex]X^{t}[/tex] × X)/n.
Learn more about Covariance Matrix here
https://brainly.com/question/30481066
#SPJ4
The given question is incomplete, the complete question is
Let X be a matrix of centered data with a column for each field in the data and a row for each sample. Then, not including a scalar multiple, how can we use matrix operations to compute the covariance matrix of the variables in the data?
Kelly went to a store to purchase a coffee pot. She will use a coupon for 20% off. She can calculate the cost before sales tax using the following expression, where c
represents the original cost of the coffee pot.
c−0.2c
Which other expression could Kelly use to calculate her cost before sales tax?
A. 0.8c
B. 1.2c
C.1.8c
D.80c
Answers
Solve for y in the two equations below using substitution.
3x - 9y = 9
-2x - 2y = 8
Answers
Answer:
C
Step-by-step explanation:
3x - 9y = 9 → (1)
- 2x +2y = 8 ( subtract 2y from both sides )
- 2x = - 2y + 8 ( divide through by - 2 )
x = y - 4
substitute x = y - 4 into (1)
3(y - 4) - 9y = 9
3y - 12 - 9y = 9
- 6y - 12 = 9 ( add 12 to both sides )
- 6y = 21 ( divide both sides by - 6 )
y = [tex]\frac{21}{-6}[/tex] = - [tex]\frac{7}{2}[/tex]