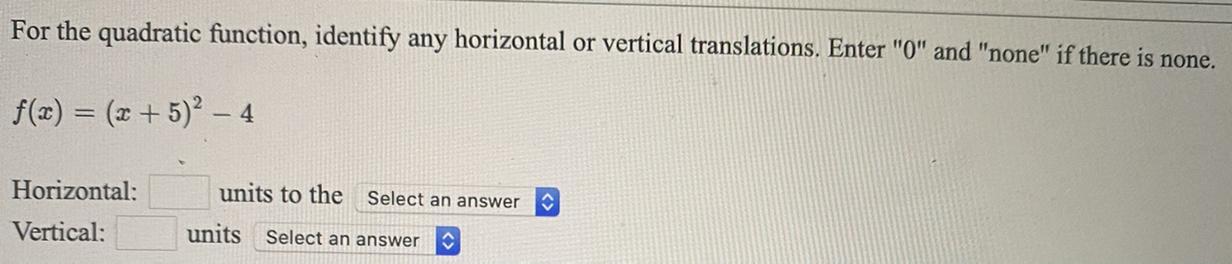
For the quadratic function, identify any horizontal or vertical translations. Enter "0" and "none" if there is none.f(x) = (x + 5)² - 4Horizontal:__ units to the (Select an answer (right, left, none)Vertical:__ units to the (Select an answer ( up, down, none)

2r + 7 = 4r - 13

subtract 4 from both-side of the equation

2r - 4r + 7 = 4r - 4r - 13

-2r + 7 = -13

subtract 7 from both-side of the equation

-2r + 7 = -13 - 7

-2r = -20

divide both-side of the equation by -2

r = 10

In summary, the respective values of the unknown variables in the equations are 42, 280, and 1800.

We have the arithmetic progression given by

if n = 1 we have the first term, n = 2 the second one and, so on, to find the 32nd term we just do n = 32, therefore

The 32nd term is 440.

Answer:

1310 cubic feet per minute

Explanation:

Let x represent the value in cubic feet per minute

Note that;

1 cubic meter per second = 2118.87997 cubic feet per minute

Given 0.618 cubic meter per second, to be able to solve for x, we'll go ahead and set the proportions as seen below;

Let's go ahead and cross-multiply;

It is required to find:

Note that any number divided by zero is undefined.

This implies that division 4/0 is undefined.

The same goes for:

The correct answer is undefined for both divisions.

Answer:

3056 can be be formed as the smallest four digit number

The vertex form of a parabola is:

where (h, k) is the vertex of the parabola and a is some constant.

From the graph, the vertex is located at (1, 4), that is, h = 1 and k = 4.

Substituting with these values and the point (0, 3), we get:

Then, the equation of the function is:

Answer:

The amount that should be invested is $1621.16

Explanation:

The formula for continuous compound interest is:

Where:

A is the amount of money after t years

P is the invested amount (what we want to find, in this case)

r is the rate of compounding in decimal

t i the amount of time compounding, in years

Then, in this case:

A = $2000

r = 0.07 (to convert percentage to decimal, we divide by 100: 7% / 100 = 0.07)

t = 3 years

Then:

To the nearest cent, P = $1621.16

The product of given complex number that is 8i and 4i will be -32 by the properties of complex number that states i*i will be -1 and 8*4 will be 32.

Every complex number can be expressed in the form a + bi, where a and b are real numbers. A complex number is an element of a number system that extends the real numbers with a specific element denoted I also known as the imaginary unit, and satisfying the equation i²=-1.

Commutative, Associative, Distributive Properties: All complex numbers are commutative and associative under addition and multiplication, and multiplication distributes over addition.

Here,

The product of 8i*4i=-32

as 8*4=32

and i²=-1

32*-1=-32

Due to the properties of complex numbers, which state that i*i will be -1 and 8*4 will be 32, the product of the given complex number, which is 8i and 4i, will be -32.

To know more about complex numbers,

https://brainly.com/question/28964590

#SPJ13

First, we need to find the sides of the triangle.

The base of the triangles is 8ft - 5ft = 3ft.

The height for the triangle is 7ft - 4ft = 3ft

Now, we need to find the area of the triangle:

Replacing the values:

Then

Now, we need to find the area for the rectangle:

Area for a rectangle = Length * Width

In this case:

Length = 8ft

Width = 7ft

Therefore:

Then

Finally, to find the area of the shaded region we need to subtract the triangle area from the rectangle area:

Therefore:

Hence, the area for the shaded region is 51.5 ft².

If he paid $57 monthly for 14 months, the total amount paid is:

He paid $798 in total

Given:

The coordinates of Quadrilateral ABCD is A(-2, 2), B(-2, 4), C(2, 4), and D(2, 2).

The quadrilateral is transformed with the rule,

It becomes,

Now, join the corresponding vertices of both the quadrilateral with the line segment.

After joining the vertices of the quadrilateral ABCD and A'B'C'D'. it gives the 3-dimensional shape- a rectangular prism.

Given:

Betsy has $400 in a personal bank account, and then withdraws $14 per

week.

Carlos has $25 in a personal bank account, and then deposits $61

earned from babysitting each week.

Required:

The same amount will they have in the bank after how many week.

Explanation:

After 5 weeks Betsy will have $330 in her account.

Since

After 5 weeks Carlos will have $330 in her account.

Since

Hence, after 5 weeks they will have the same amount of money $330 in the bank.

Final Answer:

After 5 weeks they will have the same amount of money $330 in the bank.

To find the angle measure "n", we proceed as follows:

Step 1: Recall that the sum of angles at a point is 360 degrees, as below:

Therefore, the meas

1. Divide the first term of the dividend into the first term of the divisor:

2. Multiply the result above by the divisor:

3. Subtract the result above from the divident to get a new polynomial:

4. Repeat the process with the new polynomial:

The coordinates can be obtained using section formula

The x coordinate of E is 7 and y coordinate is 8.

step 1

Find the slope m

we need two points

so

(200,100) and (80,220)

m=(220-100)/(80-200)

m=120/-20

m=-6

step 2

Find the equation of the line in point slope form

y-y1=m(x-x1)

we have

m=-6

(x1,y1)=(200,100)

substitute

y-100=-6(x-200)

Convert to slope intercept form

y-100=-6x+1200

step 3

Find the equation in standard form

Ax+By=C

where

A is a positive integer

B and C are integers

so

y=-6x+1300

The bar graph is attached below.

The heights of the rectangular bars in a bar graph, which displays complete data, are proportionate to the values they indicate. The graph's bars can be displayed either vertically or horizontally. Bar graphs, commonly referred to as bar charts, are a visual depiction of groups of data. It is one method of processing data. A bar graph is a great tool for representing data that are unrelated to one another and do not need to be displayed in any particular sequence. The bars provide a visual representation for comparing amounts in several categories. The x and y axes, commonly known as the horizontal and vertical axes, the title, labels, and a bar graph are all included.

Hence we frame the desired bar graph.

Learn more about bar graph here:

brainly.com/question/24741444

#SPJ1

For two binomials, the distributive property is:

So, let's solve this problem.

Step 01: Multiply the first term of the binomial (x - 3) by both terms of the binominal (4x + 2).

Step 02: Multiply the second term of the binomial (x - 3) by both terms of the binominal (4x + 2).

Step 03: Multiply the terms.

Step 04: Add like terms.

Answer:

In this case, we'll have to carry out several steps to find the solution.

Step 01:

Data

s = 50in

d = 20in

surface area of a cone = ?

Step 02:

surface area of a cone

SA = πr² + πrs

r = d/2 = 20in / 2 = 10in

SA = 3.14*(10in)² + 3.14*50in*10in

SA = 314in² + 1570in²

SA = 1884in²

The answer is:

SA = 1884in²

Let the number of miles I can travel for $33 be x;

The total cost of taxi ride from the airport is;

Flat fee + Tolls fee + Charge/Mile = Total cost

Flat fee = $2.00

Toll fee = $3.50

Charge per mile = 0.50x

Total cost = $33.00

Thus, we have;

Thus, the number of miles

Answer:

Explanation:

From the information given, 3

First, we compute the 16% of $850 and the 7% of $850:

Then, after deductions, Aldo gets paid $850-$136-$59.5=$654.5 biweekly. Therefore, since he gets paid biweekly we multiply $654.5 per 26 and get that Aldo earns $17017 per year.

Answer: Option C.

Answer:

-11

Step-by-step explanation:

1-4x(-3)+8x(-3)=

first you multiple

-4x(-3)=12

8x(-3)= -24

bring down the 1

1+12-24=

now we add

13-24=

then subtract and we get

-11

It could be assembled a rectangular prism

and

Solution:

Let t be the number of hours Mai works as a tutor.

Given that She earns $12 a hour as a tutor, this implies that for t number of hours, she will earn

For the month, she worked a combined total of 85 hours. This implies that

Her total eranings for the month is expressed as

Recall that she earnes $7 an hour while working as a waitress.

Thus, we have her combined total amount in dollars expressed as

Hence, the expression is

Considering this year as the last year in the table which is 2013

Therefore,

The number of students to attend this year's talent show will be calculated by

Hence.

The attendance for this year is 342 students