Answers
Answer:
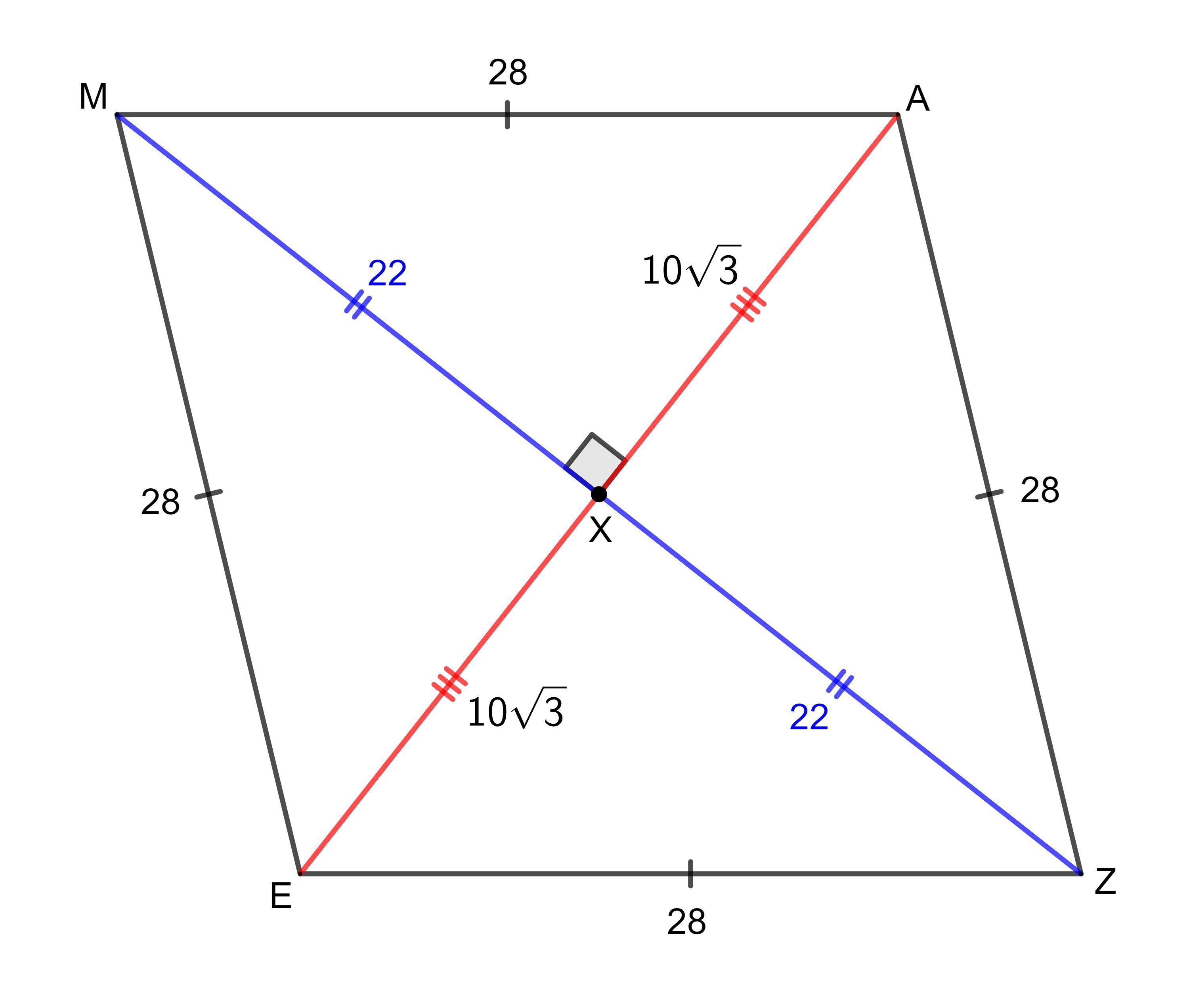
[tex]\textsf{1.}\quad \sf \overline{AZ} = 28 \; meters[/tex]
[tex]\textsf{2.}\quad \sf \overline{AM} = 28 \; meters[/tex]
[tex]\textsf{3.}\quad b = \sf 4[/tex]
[tex]\textsf{4.}\quad \sf Perimeter = 112\; meters[/tex]
[tex]\textsf{5.}\quad \sf \overline{MX} = 22\; meters[/tex]
[tex]\textsf{6.}\quad \sf \overline{AX} = 10\sqrt{3}\; meters[/tex]
[tex]\textsf{7.}\quad \sf \overline{EX} = 10\sqrt{3}\; meters[/tex]
[tex]\textsf{8.}\quad \sf \overline{AE} = 20\sqrt{3}\; meters[/tex]
Step-by-step explanation:
Side lengths and value of bAll sides of a rhombus are the same length. Therefore, for rhombus MAZE:
[tex]\sf \overline{AZ} = \overline{AM} = \overline{ZE} = \overline{EM}[/tex]
Given:
[tex]\overline{\sf AZ} =8b-4[/tex][tex]\overline{\sf AM} =5b+8[/tex]As the sides of a rhombus are the same length, we can equate the expressions for sides AZ and AM, and solve for b:
[tex]\begin{aligned}\overline{\sf AZ}&=\overline{\sf AM}\\8b-4&=5b+8\\8b-4-5b&=5b+8-5b\\3b-4&=8\\3b-4+4&=8+4\\3b&=12\\3b \div 3&=12 \div 3\\b&=4\end{aligned}[/tex]
Therefore, the value of b is 4.
To find the length of AZ and AM, substitute the found value of b into one of the expressions:
[tex]\begin{aligned}\overline{\sf AZ}&=8b-4\\&=8(4)-4\\&=32-4\\&=28\end{aligned}[/tex]
Therefore, as AZ = AM, then AZ = 28 and AM = 28.
[tex]\hrulefill[/tex]
PerimeterAs the sides of a rhombus are equal in length, each side length is 28 meters (as found previously).
The perimeter of rhombus MAZE is the sum of its side lengths. Therefore:
[tex]\begin{aligned}\sf Perimeter\;MAZE&=\sf \overline{AZ} +\overline{AM} +\overline{ZE}+ \overline{EM}\\&=28+28+28+28\\&=112\; \sf meters\end{aligned}[/tex]
Therefore, the perimeter of rhombus MAZE is 112 meters.
[tex]\hrulefill[/tex]
DiagonalsThe point of intersection of the diagonals of rhombus MAZE is point X.
As the diagonals of a rhombus are perpendicular bisectors of each other, then:
[tex]\sf \overline{AX}=\overline{EX}\quad and \quad \overline{AX}+\overline{EX}=\overline{AE}[/tex]
[tex]\sf\overline{MX}=\overline{ZX}\quad and \quad\overline{MX}+\overline{ZX}=\overline{MZ}[/tex]
Given MZ = 44 meters, and MX is half of MZ, then:
[tex]\sf \overline{MX}=\overline{ZX}=22\;meters[/tex]
As the diagonals bisect each other at 90°, m∠MXA= 90°. Therefore, ΔMXA is a right triangle with hypotenuse AM = 28 and leg MX = 22.
As we know the lengths hypotenuse AM and leg MX, we can use Pythagoras Theorem to calculate the length of the other leg, AX:
[tex]\begin{aligned}\sf \overline{AX}^2+\overline{MX}^2&=\sf \overline{AM}^2\\\sf \overline{AX}^2+22^2&=\sf 28^2\\\sf \overline{AX}^2&=\sf 28^2-22^2\\\sf \overline{AX}&=\sqrt{\sf 28^2-22^2}\\\sf \overline{AX}&=\sf 10\sqrt{3}\; meters\end{aligned}[/tex]
As the diagonals bisect each other, AX = EX. Therefore:
[tex]\sf \overline{EX}=\sf 10\sqrt{3}\; meters[/tex]
The length of diagonal AE is the sum of segments AX and EX. Therefore:
[tex]\begin{aligned}\sf \overline{AE}&=\sf \overline{AX}+\overline{EX}\\&=\sf 10\sqrt{3}+10\sqrt{3}\\&=\sf 20\sqrt{3}\; meters\end{aligned}[/tex]
[tex]\hrulefill[/tex]
Note: The attached diagram is drawn to scale.
Related Questions
Find what percentage of $6500 is $4250
Answers
Step-by-step explanation:
To find the percentage that $4250 represents of $6500, we can use the following formula:
percentage = (part / whole) x 100%
where "part" is $4250 and "whole" is $6500.
Substituting these values into the formula, we get:
percentage = (4250 / 6500) x 100%
percentage = 0.6538 x 100%
percentage = 65.38%
Therefore, $4250 represents 65.38% of $6500.
Answer: It is approximately 65%
Step-by-step explanation: Divide $4,250 by $6,500 and your answer without rounding is 65.3846%
Hodgman Honest is evaluating a new project for her firm, Basket Wonders (BW). She has determined that the after-tax cash flows for the project will be $10,000; $12,000; $15,000; $10,000; and $7,000, respectively, for each of the Years I through 5. The initial cash outlay will be $40.000. For this project, assume that it is independent of any other potential projects that Basket Wonders may undertake. The management of Basket Wonders has set a maximum PBP of 3.5 years for projects of this type. Required: Evaluate this project using payback period technique and advise the management accordingly.
Answers
Answer:
To calculate the payback period (PBP) for this project, we need to determine how long it will take for the initial cash outlay of $40,000 to be recovered from the after-tax cash flows.
Year 1 cash flow = $10,000
Year 2 cash flow = $12,000
Year 3 cash flow = $15,000
Year 4 cash flow = $10,000
Year 5 cash flow = $7,000
Total cash inflows for year 1 and year 2 = $10,000 + $12,000 = $22,000
Total cash inflows for year 3 = $15,000
Total cash inflows for year 4 = $10,000
Total cash inflows for year 5 = $7,000
Cumulative cash inflows for year 1 and year 2 = $22,000
Cumulative cash inflows for year 3 = $37,000
Cumulative cash inflows for year 4 = $47,000
Cumulative cash inflows for year 5 = $54,000
It can be seen that the cumulative cash inflows reach the initial cash outlay of $40,000 after year 2, and therefore the payback period for this project is 2 years. Since the payback period is less than the maximum PBP of 3.5 years set by management, this project can be considered acceptable.
So, Hodgman Honest should recommend that Basket Wonders should accept this project as it has a payback period of only 2 years, which is less than the maximum PBP of 3.5 years set by management.
BEAINEST IF CORRECT
if x= 60 would they be similar or not? explain ur answer.
Answers
Answer: no they wouldn't be similar
Step-by-step explanation: if x=60 if triangle 1 then the third angle would be (180-(58+60)) =180-118=62
if we decide to calculate the third angle in triangle 2 we will have 180-(50+58) = 180-108=72
therefore not all angles in 1 are similar to angles in 2 so the triangles aren't similar
1. You purchase a car using a $12,500 loan with a 5.6% simple interest rate.
(a) Suppose you pay the loan off after 6 years. How much interest do you pay on your loan? Show your work.
(a) Suppose you pay the loan off after 3 years. How much interest do you save by paying the loan off sooner? Show your work.
Answers
The interest that is paid on the loan in 6 years will be $4,200.
The amount of interest that is saved is $2,100.
What is the interest on the loan?The simple interest is a linear function of the number of years of the loan, value of the loan and the duration of the loan. The higher either of these values are, the higher the simple interest.
Simple interest = loan x time x interest rate
Simple interest if the loan is paid off after 6 years: $12,500 x 6 x 0.056 = $4,200
Simple interest if the loan is paid off after 3 years: $12,500 x 3 x 0.056 = $2100
Interest saved = $4200 - $2100 = 2100
To learn more about simple interest, please check: https://brainly.com/question/27328409
#SPJ1
Select the correct answer. The product of two numbers is 21. If the first number is -3, which equation represents this situation and what is the second number? A. The equation that represents this situation is x − 3 = 21. The second number is 24. B. The equation that represents this situation is 3x = 21. The second number is 7. C. The equation that represents this situation is -3x = 21. The second number is -7. D. The equation that represents this situation is -3 + x = 21. The second number is 18.
Answers
Answer:
The product of two numbers is 21.
Step-by-step explanation:
If the first number is -3, which equation represents this situation and what is the second number? A. The equation that represents this situation is x − 3 = 21.
which is more 7,000 millimeters or 7 liters?
Answers
I need this work sheet done in 10 minutes or less!!
Answers
Answer:
3. 216 cm^3
4a. A = 5 ft, B = 4 ft.
4b. 88 ft^3
Step-by-step explanation:
3. Separate into two rectangular prisms:
Volume of first one: 4cm*2cm*3cm = 24cm^3
Volume of second one: 4cm*12cm*4cm = 192cm^3
Add them together: 24 + 192 = 216cm^3
4a.
Length A = 8-3 = 5ft.
Width B = 8-4 = 4ft.
4b. Separate into two rectangular prisms:
Volume of first one: 2ft*3ft*4ft = 24ft^3
Volume of second one: 8ft*4ft*2ft = 64ft^3
Add them together: 24 + 64 = 88ft^3
Talitha will sell her bicycle shop to you for R250 000, with seller financing at a 6% nominal annual rate. The terms of the loan will require you to make 12 equal end-of-month payments per year for four years, and then make an additional final (balloon) payment of R50 000 at the end of the last month. What will your equal monthly payments be?
Answers
Answer:
Step-by-step explanation:
To calculate the equal monthly payments under this loan, we can use the formula for the present value of an annuity due, since the payments are due at the end of each period. The present value of the equal monthly payments can then be set equal to the loan amount of R250,000, and we can solve for the payment amount.
First, we need to calculate the present value factor for an annuity due with 12 payments per year over a four-year period, using a nominal annual rate of 6%.
PVIFA(due) = (1 - (1 + r/n)^(-nt))/((r/n)(1 + r/n))
Where:
r = nominal annual rate = 6%
n = number of compounding periods per year = 12
t = number of years = 4
PVIFA(due) = (1 - (1 + 0.06/12)^(-12*4))/((0.06/12)(1 + 0.06/12)) = 43.232
Next, we can use the formula for the present value of an annuity due to calculate the equal monthly payments:
PMT = PV / PVIFA(due)
Where:
PV = present value of the loan = R250,000
PMT = 250000 / 43.232 = R5,785.97
Therefore, your equal monthly payments will be R5,785.97. At the end of the four-year period, you will also need to make a final balloon payment of R50,000 to fully pay off the loan.
Can someone help me, please?
Answers
Formula for circumference:
C = 2 pi r
Fill it in with what’s given:
C = 2 * 3.14 * 14
Solve
= 87.92
Rounded
88in
Please helpppp it’s urgent!!! Assume you have a balance of $3000 on a credit card with an APR of 24 %, or 2 % per month. You start making monthly payments of $200, but at the same time you charge an additional $100 per month to the credit card. Assume that interest for a given month is based on the balance for the previous month. How long does it take to pay off the credit card debt? Round your numbers to the nearest cent?
Answers
It will take around 3.72 months to pay off the credit card debt.
Explain about the annual percentage rate APR?The annual rate of interest that a person must pay on a loan or receives on a bank account is known as the annual percentage rate (APR).APR is utilized for everything, including credit cards, auto loans, and mortgages.The formula for APR is:
A = P * [tex](1 + r/n)^{nt}[/tex]
In which,
A = amount after compounding.
P = balance amount
r = rate of interest.
n = number of time compounded.
Initial balance: $30,000.
Payments per month = $200.
Expenses = $100
Balance amount = 30,000 - 12 *(200 - 100)
Balance amount = $28800
So, time taken for paying off credit card debt.
30,000 = 28800 [tex](1 + 0.24/1)^{1*t}[/tex]
[tex](1.24)^{t}[/tex] = 30,000 / 28800
[tex](1.24)^{t}[/tex] = 1.04
Solve by using logarithmic function.
t = ln (1.04) / 1.24
t = 0.31 year
t = 3.72 months
Thus, it will take around 3.72 months to pay off the credit card debt.
Know more about the annual percentage rate APR
https://brainly.com/question/24715857
#SPJ1
Martha made 2 2/3 pounds of pasta. she divided the pasta into fourths. how much pasta is in each portion?
Answers
Step-by-step explanation:
2 2/3 = 8/3
8/3 * 1/4 = 8/12 = 2/3 pound in each portion
2. Evaluate the logarithmic expression using properties of logs and the change of base formula
Expression
a. log5.625
b. log6.4 +log6.12
c. log3.9^4
(i put a period after a imaginary number)
Answers
The expressions can be written as :a. log5.625 ≈ 0.75.
b. log6.4 + log6.12 ≈ 1.67.
c. log3.9^{4} ≈ 2.47.
What is logarithm function?
A logarithm function is a mathematical function that determines the power to which a fixed number, called the base, must be raised to produce a given value and The logarithm function is the inverse of the exponential function. The most commonly used base for logarithmic functions is 10 (log base 10), but other bases such as 2 (log base 2) and the natural logarithm base e (ln) are also used.
a. Since there is no base specified, we assume the base to be 10 by default. Therefore, we can write:
log5.625 = log(5625/1000)
Using the property log(a/b) = log(a) - log(b), we can simplify this expression to:
log5.625 = log(5625) - log(1000)
Using the change of base formula, we can convert the logs to a common base, such as 2 or e:
log5.625 = log(5625)/log(10) - log(1000)/log(10)
Evaluating the logs using a calculator or by simplifying, we get:
log5.625 ≈ 0.75
Therefore, log5.625 ≈ 0.75.
b. Using the property log(a) + log(b) = log(ab), we can simplify the expression:
log6.4 + log6.12 = log(6.4 × 6.12)
Using the change of base formula, we can convert this to a common base:
log6.4 + log6.12 = log(6.4 × 6.12)/log(10)
Evaluating the log using a calculator or by multiplying 6.4 and 6.12 and simplifying, we get:
log6.4 + log6.12 ≈ 1.67
Therefore, log6.4 + log6.12 ≈ 1.67.
c. Using the property log(a^{n}) = n log(a), we can simplify the expression:
log3.9^{4} = 4 log3.9
Using the change of base formula, we can convert this to a common base:
log3.9^{4} = 4 log(3.9)/log(10)
Evaluating the log using a calculator or by simplifying, we get:
log3.9^{4} ≈ 2.47
Therefore, log3.9^{4} ≈ 2.47.
To learn more about logarithm function, visit the link:
https://brainly.com/question/13473114
#SPJ1
John drives to work each morning, and the trip takes an average of µ = 38 minutes. The distribution of driving times is approximately normal with a standard deviation of σ = 5 minutes. For a randomly selected morning, what is the probability that John’s drive to work will take between 36 and 40 minutes?
Answers
The probability that John's drive to work will take between 36 and 40 minutes is 0.3413.
What is Probability?Probability is the measure of how likely an event is to occur. It is expressed as a number between 0 and 1, where 0 indicates that the event is impossible and 1 indicates that the event is certain to occur. Probability is used in many areas of life, such as gambling, finance, and science. It is also used to make decisions in everyday life, such as estimating the likelihood of rain or the chance of winning a bet.
Using the normal distribution, the probability of John's drive taking between 36 and 40 minutes can be calculated using the standard normal distribution table. The formula for calculating the probability is: P(x<X<y) = P(y) - P(x).
For the given problem, the lower boundary is 36 minutes and the upper boundary is 40 minutes. Using the standard normal distribution table, the probability of John's drive taking between 36 and 40 minutes can be calculated by subtracting the probability of 36 minutes from the probability of 40 minutes. This gives us a probability of 0.3413.
Therefore, the probability that John's drive to work will take between 36 and 40 minutes is 0.3413.
To know more about probability click-
https://brainly.com/question/24756209
#SPJ1
The probability that John's drive to work will take between 36 and 40 minutes is 0.3829.
What is Probability?Probability is the measure of how likely an event is to occur. It is expressed as a number between 0 and 1, where 0 indicates that the event is impossible and 1 indicates that the event is certain to occur. Probability is used in many areas of life, such as gambling, finance, and science. It is also used to make decisions in everyday life, such as estimating the likelihood of rain or the chance of winning a bet.
The probability that John's drive to work will take between 36 and 40 minutes can be calculated using a normal distribution table. The mean of the distribution is µ = 38 minutes, and the standard deviation is σ = 5 minutes.
To calculate the probability, we need to convert the given range (36 minutes to 40 minutes) into standard normal scores. This is done by subtracting the mean (µ = 38 minutes) from the lower bound (36 minutes) and then dividing by the standard deviation (σ = 5 minutes). The result is a standard normal score of -0.4. The same calculation is carried out for the upper bound (40 minutes) and the result is a standard normal score of 0.4.
Using a normal distribution table, we can then determine the probability that John's drive to work will take between 36 and 40 minutes. This probability is equal to the area under the normal curve between the two standard normal scores of -0.4 and 0.4. The result is a probability of 0.3829.
Therefore, the probability that John's drive to work will take between 36 and 40 minutes is 0.3829.
To know more about probability click-
brainly.com/question/24756209
#SPJ1
Which of the following equation will produce the graph shown below
Answers
The quadratic equation in the given graph can be written in the vertex-form as:
y = -2(x - 1)² + 4
Which of the equations produce the given graph?We can see the graph of a quadratic equation. Remember that a quadratic equation with a vertex (h, k) and a leading coefficient a can be written as:
y = a*(x - h)² + k
in the graph we can see that the vertex is (1, 4), replacing that we will get:
y = a*(x - 1)² + 4
In the graph we also can see that the curve passes through the point (0, 2), replacing thesevalues in the equation we will get:
2 = a*(0 - 1)² + 4
2 = a + 4
-2 = a
Then the quadratic is:
y = -2(x - 1)² + 4
Learn more about quadratic equations at:
https://brainly.com/question/1214333
#SPJ1
14 yd
21 yd find the area of the triangle
Answers
Answer:
147
Step-by-step explanation:
A= h^b b=21*14= 147
Increase the number 15/16 by 3/5 of it of it. Then increase the resulting number by 3/5 of it
Answers
The resulting number is 12/5
What are arithmetical operations?Arithmetic operations is a branch of mathematics, that involves the study of numbers, operation of numbers that are useful in all the other branches of mathematics. It basically comprises operations such as Addition, Subtraction, Multiplication and Division.
Given that we need to, increase the number 15/16 by 3/5 of it, then increase the resulting number by 3/5 of it
So, performing the operations,
15/16+15/16×3/5
= 15/16(1+3/5)
= 15/16(8/5)
= 120/80
= 3/2
Now,
3/2+3/2×3/5
= 3/2(1+3/5)
= 3/2(8/5)
= 24/10
= 12/5
Hence, the resulting number is 12/5
Learn more about arithmetical operations, click;
https://brainly.com/question/30553381
#SPJ2
15 points! please help me out!
Answers
Answer: 260 ft^2
Step-by-step explanation:
Find the area of the triangle: 0.5*height*base = 0.5*10*20 = 100 ft^2
Find the area of the rectangle: 20*8 = 160 ft^2
Add them together: 160+100 = 260 ft^2
The Revenue and Cost equations for a company are known to be polynomials of order 1 and 2 respectively. It is also known that the graphs of the two equations meet at points A(1,1) and B(5,9) while the third point of the cost function is C(2,0), obtain the following:
a) The Revenue equation and the cost equation
b) What do the common solutions to the two equations signify?
Answers
Answer: a) We know that the Revenue equation is a polynomial of order 1, so we can write it in the form:
R(x) = ax + b
where a and b are constants to be determined. We also know that R(1) = 1 and R(5) = 9, so we have two equations:
a(1) + b = 1
a(5) + b = 9
Solving these equations simultaneously, we get:
a = 2, b = -1
Therefore, the Revenue equation is:
R(x) = 2x - 1
Similarly, the Cost equation is a polynomial of order 2, so we can write it in the form:
C(x) = ax^2 + bx + c
where a, b, and c are constants to be determined. We know that C(1) = R(1) = 1 and C(5) = R(5) = 9, so we have two equations:
a(1)^2 + b(1) + c = 1
a(5)^2 + b(5) + c = 9
We also know that C(2) = 0, so we have a third equation:
a(2)^2 + b(2) + c = 0
Solving these equations simultaneously, we get:
a = 1, b = -4, c = 4
Therefore, the Cost equation is:
C(x) = x^2 - 4x + 4
b) The common solutions to the Revenue and Cost equations represent the production level(s) at which the company makes a profit, since the Revenue equation represents the amount of money the company earns and the Cost equation represents the amount of money the company spends. In other words, the common solutions are the values of x for which R(x) - C(x) > 0. At these production levels, the company's revenue is greater than its cost, resulting in a profit. At production levels where R(x) - C(x) < 0, the company is making a loss. At production levels where R(x) - C(x) = 0, the company is breaking even. Therefore, the common solutions to the two equations signify the production levels at which the company makes a profit or breaks even.
Step-by-step explanation:
how do i solve this problem?
Answers
Option A correctly describes the area of the graph of the function.
How is an area of the graph calculated?
The area of a graph is the area under the function curve enclosed within the X-axis of the graph. Thus, it is the area of the figure formed by enclosing the function graph with the X-axis.
It is the integration of the function polynomial of the possible values of x that the function curve lies in.
Here the function equation is : [tex]f(x) = ( 25 - x^{2} )[/tex]
From the figure, we can see that the value of x varies from -5 to 5.
Initial x-value of integration = minimum value of x
= -5
Final x-value of integration = maximum value of x
= 5
Thus, the area of the graph can be correctly calculated as. :
[tex]Area = \int\limits^{maxX}_ {minX} \, f(x)dx[/tex]
[tex]Area = \int\limits^5_ {-5} \, (25-x^{2} )dx[/tex]
Hence, Option A correctly calculates the area of the graph given.
To learn more about Graphs, visit
https://brainly.com/question/29548482
#SPJ1
Represent the following sentence as an algebraic
expression, where "a number" is the letter x. You
do not need to simplify.
9 less than six times a number.
Answers
Algebraic expressions are useful for solving different and complex equations in mathematics, as well as for modelling real-life situations such as revenue, cost, inference, etc
The algebraic expression is: [tex]6x - 9[/tex].
What is the use of algebraic expression?To represent the sentence as an algebraic expression, we can follow these steps: Identify the variable. In this case, “a number” is x. Identify the operation. In this case, “less than” means subtraction and “times” means multiplication.
An algebraic expression is an expression that contains variables, constants and mathematical operations. Algebraic expressions are useful because they can help us solve different and complex equations.
For example, if you want to calculate the area of a rectangle with length x and width y, you can use the algebraic expression xy to represent the area.
Write the expression using the order of operations. In this case, we need to multiply six by x first, then subtract nine from the result.
Therefore, The algebraic expression is: [tex]6x - 9[/tex]
Learn more about expression here:
https://brainly.com/question/953809
#SPJ1
A brick of mass 2 kg falls through water with an acceleration of 2 ms 2. The total force of the resistance is N.
Answers
The calculated value of the force of the resistance is 15.62 N
Calculate the force of the resistanceWe can use Newton's Second Law of Motion to solve this problem. The formula is:
F = m*a
where F is the net force, m is the mass of the object, and a is the acceleration.
In this case, the brick is falling through water, so there are two forces acting on it:
gravity (pulling it down) water resistance (slowing it down).The net force is the difference between these two forces:
F_net = F_gravity - F_resistance
The weight of the object is:
F_gravity = m*g
So, we have
F_gravity = 2 kg * 9.81 m/s^2 = 19.62 N
Now we can use the formula for net force to find the force of water resistance:
F_net = F_gravity - F_resistance
F_resistance = F_gravity - F_net
F_resistance = 19.62 N - m*a
This gives
F_resistance = 19.62 N - 2 kg * 2 m/s^2 = 15.62 N
Therefore, the force of water resistance is 15.62 N.
Read more about force at
https://brainly.com/question/13370981
#SPJ1
The diameter of the base of a cone is shown on the grid. Each square unit on the grid has a side length of 1 foot. The volume of the cone is approximately 200.96 cubic feet. Determine the height of the cone, and construct it vertically on the grid with respect to the center of the cone's base.
Use 3.14 for .
Answers
Answer:
First, we need to find the radius of the base of the cone. We can see from the grid that the diameter is 8 units, so the radius is 4 units (or 4 feet).
Next, we can use the formula for the volume of a cone to find the height:
V = (1/3)πr^2h
Substituting the given volume and radius, and using 3.14 for π, we get:
200.96 = (1/3) x 3.14 x 4^2 x h
Simplifying and solving for h, we get:
h = 200.96 / (1/3 x 3.14 x 4^2)
h = 200.96 / 53.02
h ≈ 3.79 feet (rounded to two decimal places)
To construct the cone vertically on the grid with respect to the center of the base, we can draw a circle with radius 4 units (or 4 feet) centered at the point (4,4) on the grid. Then, we can draw a line from the center of the circle (point (4,4)) up to a point above the circle that is 3.79 units (or 3.79 feet) away from the center. This line represents the height of the cone. Finally, we can connect the endpoint of the line to the points where the circle intersects the grid to complete the cone.
Resolve partially
3x+2/(x+1)(x²+x+2)
Answers
Answer:
The given expression is:
3x + 2 / (x + 1)(x² + x + 2)
To simplify this expression, we need to factor the denominator first:
x² + x + 2 = (x + 2)(x + 1)
So the expression becomes:
3x + 2 / (x + 1)(x + 2)(x + 1)
Next, we can use partial fraction decomposition to express the expression in terms of simpler fractions. Let's assume:
3x + 2 / (x + 1)(x + 2)(x + 1) = A/(x + 1) + B/(x + 2) + C/(x + 1)²
Multiplying both sides by the common denominator, we get:
3x + 2 = A(x + 2)(x + 1) + B(x + 1)² + C(x + 2)(x + 1)
Expanding the right side, we get:
3x + 2 = Ax² + 3Ax + 2A + Bx² + 2Bx + B + Cx² + 3Cx + 2C
Combining like terms, we get:
3x + 2 = (A + B + C)x² + (3A + 2B + 3C)x + (2A + B + 2C)
Since this equation holds for all values of x, the coefficients of each power of x must be equal on both sides. We can equate the coefficients of x², x, and the constant term to get a system of three equations for A, B, and C:
A + B + C = 0
3A + 2B + 3C = 3
2A + B + 2C = 2
Solving this system, we get:
A = 2/3
B = -1/3
C = -1/3
Substituting these values back into the partial fraction decomposition equation, we get:
3x + 2 / (x + 1)(x² + x + 2) = 2/3/(x + 1) - 1/3/(x + 2) - 1/3/(x + 1)²
Therefore, the simplified expression is:
3x + 2 / (x + 1)(x² + x + 2) = 2/3/(x + 1) - 1/3/(x + 2) - 1/3/(x + 1)²
12000 x 5 = 9500 + 9500 + 10000 + x + y
Answers
Answer:
31000 - y = x
Step-by-step explanation:
Solve for x
[tex]12000\times5=9500+9500+10000+x+y[/tex]
Add and multiply the integers
[tex]60000=29000+x+y[/tex]
Subtract 29000 on both sides
[tex]31000=x+y[/tex]
Subtract y on both sides
[tex]31000-y=x[/tex]
Question 2
(03.01 LC)
Which of the following is not created when a plane slices through a cone?
O Point
O Line
O Circle
O Square
Answers
A square is not created when a plane slices through a cone.
What is square?
A square is a geometrical shape that has four equal sides and four equal angles of 90 degrees.
What is cone?
A cone is a three-dimensional geometric shape that tapers smoothly from a flat base to a pointed top or apex. It looks like a funnel or an ice cream cone.
According to given information:When a plane intersects or slices through a cone, it creates a variety of different shapes depending on the angle of the plane and the position of the cone.
If the plane intersects the cone at an angle perpendicular to its base, it will create a circle. If the plane intersects the cone at an angle that is not perpendicular to its base, it will create an ellipse.
If the plane intersects the cone at an angle that is parallel to one of its generators (the lines that can be drawn from the vertex of the cone to any point on its base), it will create a parabola. If the plane intersects the cone at an angle that is not parallel to one of its generators, it will create a hyperbola.
Therefore, a square is not created when a plane slices through a cone.
To learn more about cone visit:
https://brainly.com/question/1082469
#SPJ9
D
L
F
DM = 8
M
K
FM = 2x
E
EM = 6
Answers
Answer: yes correct i love math
Step-by-step explanation:
The slope of a line is undefined, and the x-intercept is -7. What is the equation of the line?
Oy=-7
Ox=-7
Oy=-7x
Answers
Answer:
"Undefined slope"
Step-by-step explanation:
The line is vertical on the graph.
Every point on the line has the same x-coordinate.
If the line crosses the x-axis where x=-7, then the
x-coordinate of every point on the line is -7, and the
equation of the line is
x = -7 .
A company estimates that 0.8% of their products will fail after the original warranty period but within 2 years of the purchase, with a replacement cost of $200.
If they offer a 2 year extended warranty for $22, what is the company's expected value of each warranty sold?
$
Answers
Therefore , the solution of the given problem of percentage comes out to be the firm expects that each warranty it sells will be worth $1.41.
What is percentage?In statistics, "a%" is used to refer to a figure or number that is expressed as a percentage of 100. Additionally rare are the forms that "pct," "pct," or "pc". It is typically represented by the symbol "%," though. Additionally, there are not any indicators and the proportion of each item to the overall amount is flat. Since percentages typically add up to 100, they are essentially integers. Either the expression "fraction" or the symbol for percentage (%) .
Here,
The price to substitute each item is $200. The anticipated price for each component is thus:
Expected cost per product equals Replacement cost x Failure Probability
=> Cost per product anticipated = 0.008 x $200
=> Expected price per item is $1.60.
So, the following is the anticipated value of each warranty sold:
Expected worth of the warranty = Failure rate x (Replacement cost - Cost of warranty)
=> Expected guarantee value = 0.008 * ($200 - $22 - $1.60).
=> Expected guarantee value = 0.008 * $176.40
=> Expected warranty worth is $1.41
As a result, the firm expects that each warranty it sells will be worth $1.41.
To know more about percentage visit:
https://brainly.com/question/28269290
#SPJ1
Find the probability of rolling an even number on a single die
Answers
The probability of rolling an even number on a single die is 1/2, or 50%. This can be calculated by considering the possible outcomes of rolling the die.
There are six possible outcomes, and three of these are even numbers (2, 4, and 6). Therefore, there is a 3/6, or 1/2, chance of rolling an even number. In terms of probability, this can be expressed as a fraction, percentage, or decimal. As a fraction, the probability of rolling an even number on a single die is 3/6, or 1/2. As a percentage, the probability of rolling an even number on a single die is 50%. As a decimal, the probability of rolling an even number on a single die is 0.5. No matter how it is expressed, the probability of rolling an even number on a single die is 1/2, or 50%. This can be easily remembered by considering that there are six possible outcomes, and three of them are even numbers.
Learn more about probability here:
https://brainly.com/question/15124899
#SPJ1
i dont get it help me
Answers
Answer:
y=2x+10
Explanation: They start with paying $10 and have to pay and extra $2 for each time at the concession stand.
