Answers
Answer:
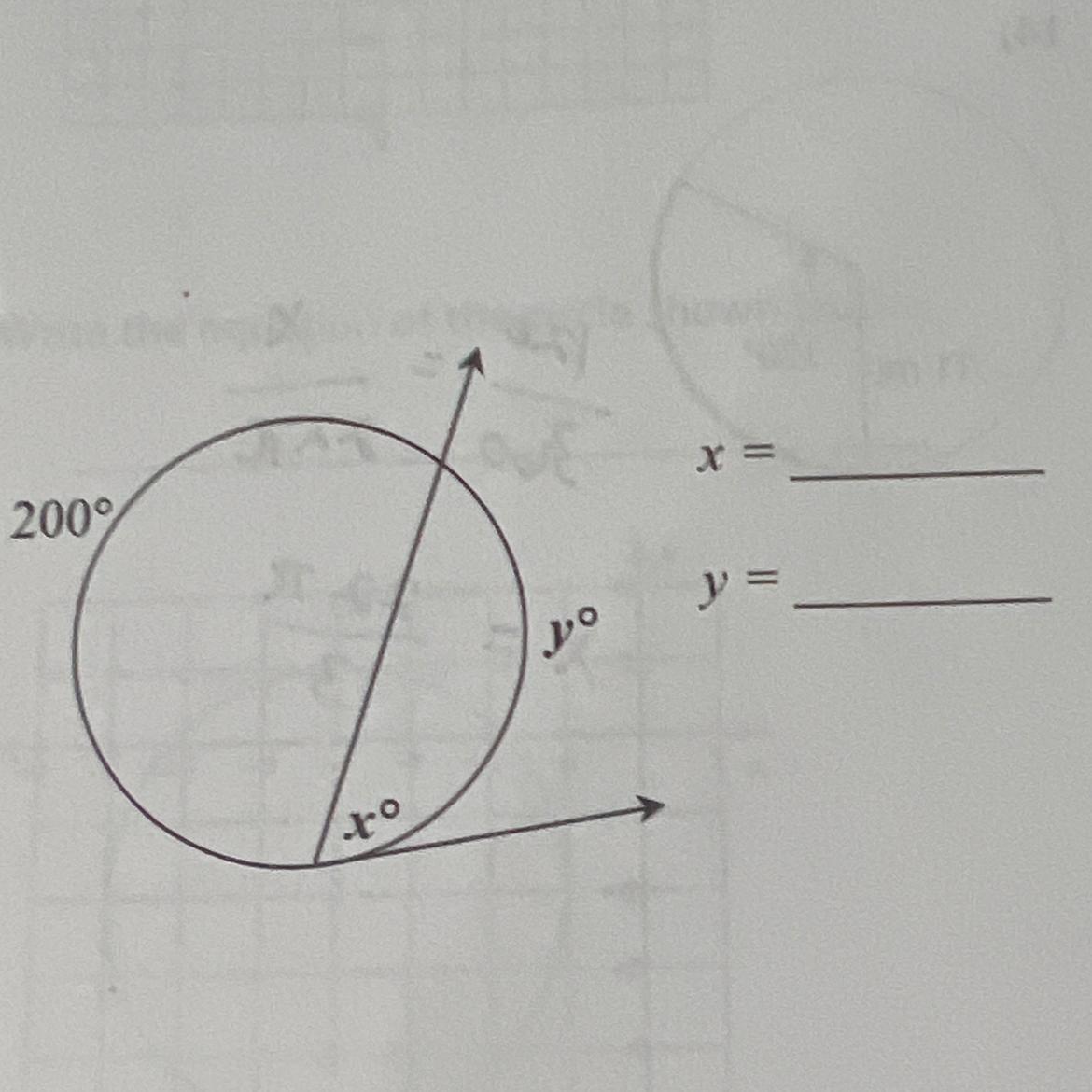
x = 80
y = 160
Step-by-step explanation:
The sum of all arc measures that make up a circle is 360°. Therefore:
[tex]\implies 200^{\circ} + y^{\circ} = 360^{\circ}[/tex]
[tex]\implies 200^{\circ} + y^{\circ} - 200^{\circ} = 360^{\circ} - 200^{\circ}[/tex]
[tex]\implies y^{\circ} = 160^{\circ}[/tex]
[tex]\implies y=160[/tex]
Tangent and Intersected Chord TheoremIf a tangent and a chord intersect at a point on a circle, then the measure of each angle formed is one-half the measure of its intercepted arc.
Therefore, according to the Tangent and Intersected Chord Theorem, the measure of angle x is equal to half of the measure of arc y:
[tex]\implies x^{\circ}=\dfrac{1}{2} y^{\circ}[/tex]
[tex]\implies x^{\circ}=\dfrac{1}{2} \cdot 160^{\circ}[/tex]
[tex]\implies x^{\circ}=80^{\circ}[/tex]
[tex]\implies x=80[/tex]
[tex]\hrulefill[/tex]
Circle Theorem vocabularyChord: A straight line joining two points on the circle.Tangent: A straight line that touches a circle at only one point.Arc: the curve between two points on the circumference of a circleIntercepted arc: The curve between the points where two chords or line segments intercept the circumference of a circle.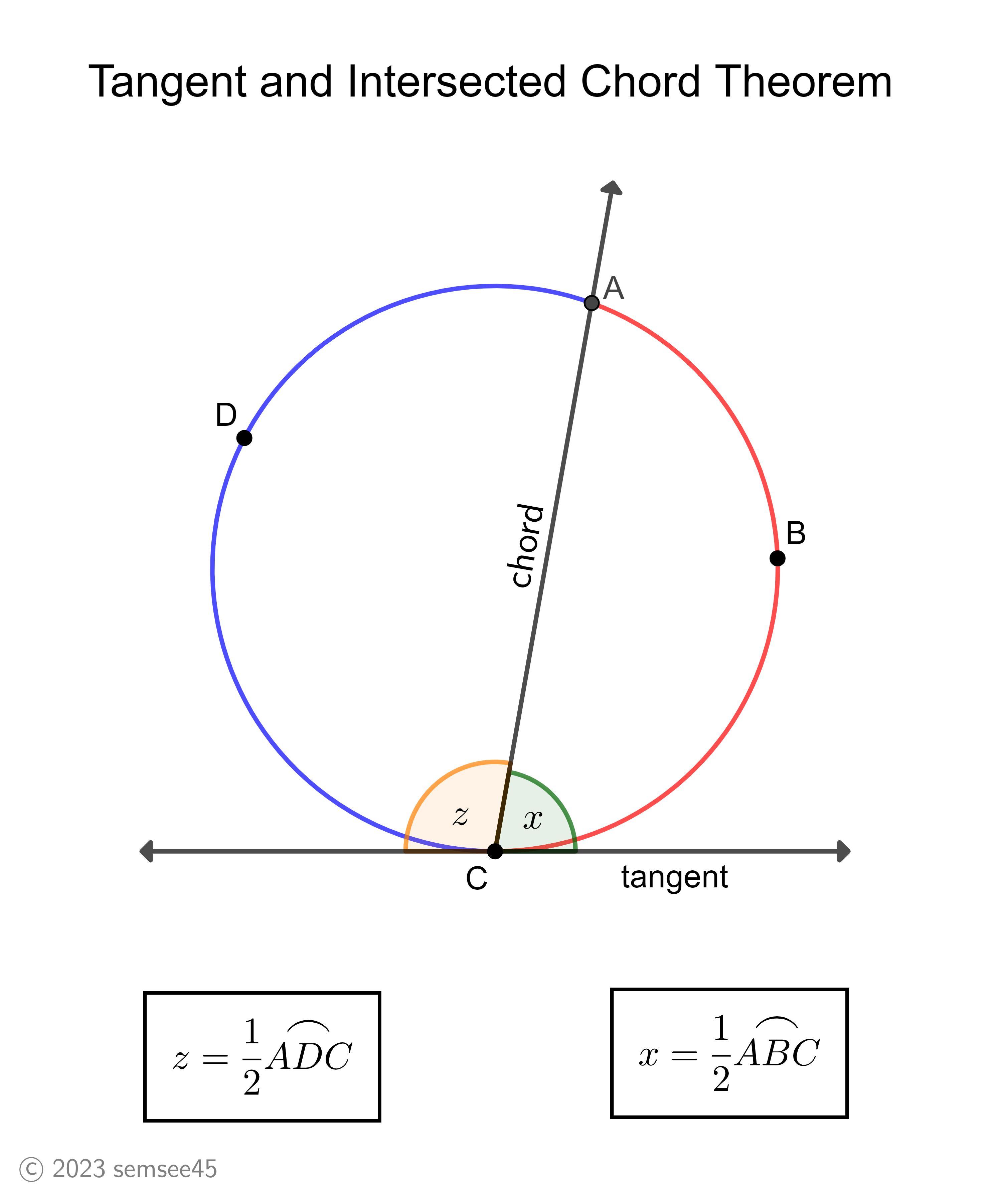
Related Questions
Write ^4√11^5 without radicals.
Answers
Answer: ^4√11^5 = 11^(5/4)
Step-by-step explanation: When we apply a radical, we are asking what number, when raised to a certain power, gives us the number under the radical. For example, ^4√16 is asking what number, when raised to the fourth power, gives us 16. The answer is 2, since 2^4 = 16.
So, ^4√11^5 is asking what number, when raised to the fourth power, gives us 11^5. We can simplify this expression using the exponent laws:
^4√11^5 = (11^5)^(1/4) = 11^(5/4)
Therefore, the simplified expression for ^4√11^5 is 11^(5/4). This expression does not have any radicals, making it easier to work with and manipulate.
Hope this helps, and have a great day!
Can you help me with this
Answers
Answer:c
Step-by-step explanation:
Answer: C
Step-by-step explanation:
13. security y has the following returns over five years: 3%, 6%, 0%, 6%, and 3%. what is the arithmetic mean (average) return and the standard deviation (sample) for security y?
Answers
The arithmetic mean return is 3.6%, and the standard deviation is 2.14%.
To find the arithmetic mean, we add up the five returns and divide by the number of returns (in this case, 5):
(3% + 6% + 0% + 6% + 3%) / 5 = 3.6%
To find the standard deviation, we first need to find the variance. We can do this by taking each return, subtracting the mean return (3.6%), squaring the result, summing these values, and dividing by the number of returns minus 1 (4 in this case):
((3% - 3.6%)^2 + (6% - 3.6%)^2 + (0% - 3.6%)^2 + (6% - 3.6%)^2 + (3% - 3.6%)^2) / 4 = 0.046
The standard deviation is the square root of the variance:
√0.046 = 0.214 or 2.14%
Therefore, the arithmetic mean return for security y is 3.6%, and the standard deviation (sample) is 2.14%.
To know more about arithmetic mean, refer here:
https://brainly.com/question/13000783#
#SPJ11
Any number that can be written as a decimal, write as a decimal to the tenths place.
Given A = (-3,2) and B = (7,-10), find the point that partitions segment AB in a 1:4 ratio.
The point that partitions segment AB in a 1:4 ratio is (
).
Answers
The point that partitions segment AB in a 1:4 ratio is [tex]P = \left(-1, -\frac{2}{5}\right)$[/tex].
How to find the ratio?To find the point that partitions segment AB in a 1:4 ratio, we can use the section formula.
Let P = (x, y) be the point that partitions segment AB in a 1:4 ratio, where AP:PB = 1:4. Then, we have:
[tex]$\frac{AP}{AB} = \frac{1}{1+4} = \frac{1}{5}$$[/tex]
and
[tex]$\frac{PB}{AB} = \frac{4}{1+4} = \frac{4}{5}$$[/tex]
Using the distance formula, we can find the lengths of AP, PB, and AB:
[tex]AP &= \sqrt{(x+3)^2 + (y-2)^2} \\PB &= \sqrt{(x-7)^2 + (y+10)^2} \\\ AB &= \sqrt{(7+3)^2 + (-10-2)^2} = \sqrt{244}[/tex]
Substituting these into the section formula, we have:
[tex]$\begin{aligned}x &= \frac{4\cdot(-3) + 1\cdot(7)}{1+4} = -1 \ y &= \frac{4\cdot2 + 1\cdot(-10)}{1+4} = -\frac{2}{5}\end{aligned}$$[/tex]
Therefore, the point that partitions segment AB in a 1:4 ratio is [tex]P = \left(-1, -\frac{2}{5}\right)$[/tex].
To know more about Segment visit;
brainly.com/question/30161863
#SPJ1
a horizontal curve is to be designed with a 2000 feet radius. the curve has a tangent length of 400 feet and its pi is located at station 103 00. determine the stationing of the pt.
Answers
A horizontal curve is to be designed with a 2000 feet radius. The curve has a tangent length of 400 feet and its pi is located at station 103+00. Determine the stationing of the PT.
A horizontal curve is a curve that is used to provide a transition between two tangent sections of a roadway. To connect two tangent road sections, horizontal curves are used. Horizontal curves are defined by a radius and a degree of curvature. The curve's radius is given as 2000 feet. The tangent length is 400 feet.
The pi is located at station 103+00.
To determine the stationing of the PT, we must first understand what the "pi" means. PC or point of curvature, PT or point of tangency, and PI or point of intersection are the three primary geometric features of a horizontal curve. The point of intersection (PI) is the point at which the back tangent and forward tangent of the curve meet. It is an important point since it signifies the location of the true beginning and end of the curve. To calculate the PT station, we must first determine the length of the curve's arc. The formula for determining the length of the arc is as follows:
L = 2πR (D/360)Where:
L = length of the arc in feet.
R = the radius of the curve in feet.
D = the degree of curvature in degrees.
PI (103+00) indicates that the beginning of the curve is located 103 chains (a chain is equal to 100 feet) away from the road's reference point. This indicates that the beginning of the curve is located 10300 feet from the road's reference point. Now we need to calculate the degree of curvature
:Degree of curvature = 5729.58 / R= 5729.58 / 2000= 2.8648 degrees. Therefore, the arc length is:
L = 2πR (D/360)= 2π2000 (2.8648/360)= 301.6 feet.
The length of the curve's chord is equal to the length of the tangent, which is 400 feet. As a result, the length of the curve's long chord is: Long chord length = 2R sin (D/2)= 2 * 2000 * sin(2.8648/2)= 152.2 feet To determine the stationing of the PT, we can use the following formula: PT stationing = PI stationing + Length of curve's long chord= 10300 + 152.2= 10452.2Therefore, the stationing of the PT is 10452+2.
A horizontal curve is to be designed with a 2000 feet radius : https://brainly.com/question/31078631
#SPJ11
in 2005 the population of a district was 35,700 with a continuous annual growth rate of approximately 4%, what will the population be in 2030 according to the exponential growth function?
Answers
The population of a district in 2005 was 35,700 with a continuous annual growth rate of approximately 4%. the population in 2030 will be approximately 97,209 according to the exponential growth function.
The formula for the continuous exponential growth is given by the formula:
P = Pe^(rt)
where,P is the population in the future.
P0 is the initial population.
t is the time.
r is the continuous interest rate expressed as a decimal.
e is a constant equal to approximately 2.71828.In this problem, the initial population P0 is 35,700. The rate r is 4% or 0.04 expressed as a decimal. We want to find the population in 2030, which is 25 years after 2005.
Therefore, t = 25.We will now use the formula:
P = Pe^(rt)P = 35,700e^(0.04 × 25)P = 35,700e^(1)P = 35,700 × 2.71828P = 97,209.09.
for such more question on population
https://brainly.com/question/25630111
#SPJ11
Answer: I got 97,042.7
Step-by-step explanation:
9. The linear regression equation is = 34.38x - 91.75. Use the equation to predict how far this
4.38x-91-75 Use
person will travel after 10 hours of driving.
Answers
The answer of the given question based on the linear regression is , the predicted distance the person will travel after 10 hours of driving is approximately 252.05 miles.
What is Distance?Distance is measurement of length between the two points or objects. It is a scalar quantity that only has a magnitude and no direction. In mathematics, distance can be measured in various units such as meters, kilometers, miles, or feet, depending on the context.
Distance can be calculated using the distance formula, which is based on the Pythagorean theorem in two or three dimensions.
Assuming the equation you meant to write is y = 34.38x - 91.75, where y is the predicted distance traveled in miles and x is the number of hours driven, we can use this equation to predict how far the person will travel after 10 hours of driving:
y = 34.38x - 91.75
y = 34.38(10) - 91.75
y = 343.8 - 91.75
y = 252.05
Therefore, the predicted distance the person will travel after 10 hours of driving is approximately 252.05 miles.
To know more about Equation visit:
https://brainly.com/question/9312365
#SPJ9
During 10 hours of driving, the projected distance according to linear regression is roughly 252.05 miles.
What is Distance?The term "distance" refers to the length between two points or objects. Having merely a magnitude and no direction, it is a scalar quantity. Depending on the situation, distance in mathematics can be expressed in a variety of ways, including meters, kilometers, miles, or feet.
The distance formula, which depends on the Pythagorean theorem in either two or three dimensions, can be used to compute distance.We may use this equation to forecast how far the individual would go after 10 hours of driving, assuming the equation you meant to write is
y = 34.38x - 91.75, where y is the expected distance travelled in miles and x is the number of hours driven:
y = 34.38x - 91.75
y = 34.38(10) - 91.75
y = 343.8 - 91.75
y = 252.05
The estimated distance that the driver will cover after 10 hours on the road is 252.05 miles.
To know more about linear regression, visit:
https://brainly.com/question/30063703
#SPJ9
The complete question is,
The equation for linear regression is = 34.38x - 91.75. Calculate this person's estimated distance after 10 hours of driving using the equation: 4.38x-91-75.
A sphere has a radius of 9in. the sphere is cut in half. what is the volume of each hemisphere. use 3.14 for pi and round to the hundredths if needed. Show work. PLEASE ANSWER IT
Answers
V = (4/3)πr³
where V is the volume of the sphere, r is the radius, and π is the constant pi (3.14).
To find the volume of each hemisphere, we need to find the volume of the entire sphere and then divide it by 2. The volume of the entire sphere is:
V = (4/3)πr³
V = (4/3)π(9in)³
V = (4/3)π(729in³)
V = 3053.63in³ (rounded to the hundredths)
Now, to find the volume of each hemisphere, we divide this value by 2:
V = 3053.63in³ ÷ 2
V = 1526.82in³ (rounded to the hundredths)
Therefore, the volume of each hemisphere is approximately 1526.82 cubic inches.
Please help!!
The mayoral election results for the town of Gainesville are shown in the table below.
Election Results for Jainsville
30 and Under
31-40
41-50
51-60
61-70
71 and Over
New
Conservative Democratic Liberal
3,112
1,213
1,991
2,313
1,101
1,233
1,445
422
874
423
899
75
343
623
713
1,134
1,221
2,346
Voters were able to vote for one of three candidates, each represented by one of the three
parties shown in the table. Each voter was given a six-digit identification number. What is the
probability that if an identification number is randomly chosen, a 50-year-old or older voter from
the winning party will be chosen from the pool of voters? Round your answer to the nearest
hundredth of a percent.
Answers
The probability of randomly chosen, a 50-year-old or older voter from the winning party is 45.84%
The probability of randomly chosen, a 50-year-old or older voterGiven the table of values
From the table of values, we have the winning party to be
New Democratic
From the column of New Democratic, we have
Total = 9422
50-year-old or older voter = 4319
So, the required probability is
Probbaility = 4319/9422
Evaluate
Probbaility = 0.45839524517
This gives
Probbaility = 45.839524517%
Approximate
Probbaility = 45.84%
Hence, the probability is 45.84%
Read more about probability at
https://brainly.com/question/24756209
#SPJ1
Which relationships describe angles 1 and 2?
Select each correct answer.
adjacent angles
complementary angles
vertical angles
supplementary angles
Answers
Answer:
1+2=90° .so complementary angle
Can anyone please help 10 points
Answers
The value of x using similar triangles theorem is = 13/3.
What are similar triangles?Triangles that resemble one another but may not be exactly the same size are said to be comparable triangles.
When two objects have the same shape but different sizes, they can be said to be comparable.
This indicates that comparable shapes superimpose one another when amplified or de-magnified.
The term "Similarity" refers to this characteristic of like shapes.
Now in the given figure,
the proportion of the triangles' side is same.
So, 12/4 = 13/x
x = 13/3
To know more about similar triangles, visit:
https://brainly.com/question/30725762
#SPJ1
in a congressional district, 55% of the registered voters are democrats. which of the following is equivalent to the probability of getting less than 50% democrats in a random sample of size 100?
A. P( z< 50 — 55/ 100 )
B. P( z< 50 — 55/ √55(45)/100)
C. P( z< 55 — 5 / √55(45)/100)
D. P( z< 50 — 55/√100(55) (45))
Answers
The correct answer to the question, "Which of the following is equivalent to the probability of getting less than 50% democrats in a random sample of size 100?" is: B. P( z < 50 — 55/ √55(45)/100).
To find the probability, we first calculate the z-score using the formula:
z = (x - μ) / σ
where x is the value (50%), μ is the mean (55%), and σ is the standard deviation.
The standard deviation can be calculated as:
σ = √(np(1-p))
where n is the sample size (100) and p is the proportion of democrats (0.55).
Now, plug in the values into the z-score formula:
z = (50 - 55) / √(100 * 0.55 * 0.45)
The probability is then found as P(z < z-score), which is represented by the option B.
More On Probability: https://brainly.com/question/24756209
#SPJ11
Describe each number at least one other way. A)35. 8 million
b)115. 2 thousands
c)97. 8 ten millions
Answers
A) 35. 8 million; thirty-five million eight hundred thousand, or thirty-five million eight hundred thousand dollars ,(b)115. 2 thousand; one hundred and fifteen thousand two hundred.(c) 97.8 million eight hundred thousand; 97.8 million eight hundred thousand. or 978 million.
What significance do numbers have?
We need good numeracy skills as parents to assist our children to develop, as patients to grasp healthcare information, and so as politicians to make sense of numbers and economic news. Selections in life were frequently based upon numerical data; in order to arrive at optimal decisions, we must be good at maths.
How are numbers used in everyday life?
Numbers are utilized in a variety of mathematical operations such as summation, subtraction, multiplication, division, percentage, and so on, that we employ in the everyday companies and exchanges. Quantities are numerical symbols representing integers that may be used for numbering, estimating, and doing other arithmetic operations.
To know more about integers click here
brainly.com/question/10930045
#SPJ4
Pls help answer with good detailed explanation
Answers
Mr. Kha Lipat wants to earn 8% on his investment. How much money should he invest today in order to receive 400. 00 one year from now?
Answers
Mr. Kha Lipat should invest $5,000 today in order to receive $400.00 in interest one year from now at an 8% interest rate.
To calculate how much money Mr. Kha Lipat should invest today to receive $400.00 one year from now at an 8% interest rate, we can use the formula for calculating simple interest though compound intrest:
I = P * r * t
where I is the interest earned, P is the principal (the initial amount invested), r is the interest rate (as a decimal), and t is the time period (in years).
We know that Mr. Kha Lipat wants to earn $400.00 in interest, the interest rate is 8% or 0.08 (as a decimal), and the time period is 1 year. We can plug these values into the formula and solve for P:
I = P * r * t
400 = P * 0.08 * 1
400 = 0.08P
P = 400 / 0.08
P = 5000
Therefore, Mr. Kha Lipat should invest $5,000 today in order to receive $400.00 in interest one year from now at an 8% interest rate.
To learn more about interest Click here:
brainly.com/question/30955042
#SPJ4
Solve the equation
1/4xln(16q^8)-ln3=ln24
Answers
We can claim that after answering the above question, the Therefore, the solution to the original equation is: [tex]q = 9^x\\[/tex]
What is equation?In mathematics, an equation is a statement that states the equality of two expressions. An equation consists of two sides separated by an algebraic equation (=). For example, the argument "2x + 3 = 9" states that the sentence "2x Plus 3" equals the value "9". The goal of solving equations is to find the value or values of the variable(s) that will allow the equation to be true. Equations can be simple or complex, linear or nonlinear, and contain one or more parts. For example, in the equation "x2 + 2x - 3 = 0," the variable x is raised to the second power. Lines are used in many areas of mathematics, including algebra, calculus, and geometry.
given equation:
[tex]1/4xln(16q^8) - ln3 = ln24\\1/4xln(16q^8) = ln(24 * 3)\\1/4xln(16q^8) = ln72\\ln(16q^8)^(1/4x) = ln72\\16q^8^(1/4x) = 72\\16q^8 = 72^(4x)\\ln(16q^8) = ln(72^(4x))\\[/tex]
[tex]ln(16) + ln(q^8) = 4x ln(72)\\ln(q^8) = 4x ln(72) - ln(16)\\ln(q^8) = ln(72^(4x)) - ln(16^1)\\ln(q^8) = ln((72^(4x))/16)\\q^8 = e^(ln((72^(4x))/16))\\q^8 = (72^(4x))/16\\q^8 = 9^(8x)\\q = 9^x\\[/tex]
Therefore, the solution to the original equation is:
[tex]q = 9^x\\[/tex]
To know more about equation visit:
https://brainly.com/question/649785
#SPJ1
2x + y = -7
3x = 6 + 4y
x = ?
y = ?
Answers
2x + y = -7
y= -7-2x
put this value in 2nd equation
3x=6+4(-7-2x)
3x=6-28-8x
11x= -22
x= -2
y= -7-2(-2)
y= -7+4
y= -3
Write the equation of the parabola which has its vertex at (0, 5) and passes through the point (1, 0)
Answers
y = -5x² + 5 is the equation of the parabola which has its vertex at (0, 5) and passes through the point (1, 0)
We know that the vertex of the parabola is (0, 5), which means that the equation for the parabola has the form:
y = a(x - 0)² + 5
where 'a' is a constant that determines the shape of the parabola. Since the parabola passes through the point (1, 0), we can substitute these values into the equation and solve for 'a':
0 = a(1 - 0)² + 5
0 = a + 5
a = -5
Therefore, the equation of the parabola is: y = -5x² + 5
This equation represents a parabola that opens downwards (since the coefficient of x² is negative), has a vertex at (0, 5), and passes through the point (1, 0).
To learn more about parabola click here
brainly.com/question/31142122
#SPJ4
What percentage of people would exed to score higher than a 2.5, but lower than 3.5? The mean: X=3.00 The SDis= + 0.500 18% 999 o 50% 03%
Answers
Therefore, approximately 68.26% of people are expected to score higher than 2.5 but lower than 3.5.
Based on the information provided, the mean (X) is 3.00 and the standard deviation (SD) is 0.50. To find the percentage of people expected to score higher than 2.5 but lower than 3.5, we will use the standard normal distribution (z-score) table.
First, we need to calculate the z-scores for both 2.5 and 3.5:
z1 =[tex] (2.5 - 3.00) / 0.50 = -1.0[/tex]
z2 = [tex](3.5 - 3.00) / 0.50 = 1.0[/tex]
Now, we can use the standard normal distribution table to find the probability of the z-scores. For z1 = -1.0, the probability is 0.1587 (15.87%). For z2 = 1.0, the probability is 0.8413 (84.13%).
To find the percentage of people expected to score between 2.5 and 3.5, subtract the probability of z1 from the probability of z2:
Percentage = [tex](0.8413 - 0.1587) x 100 = 68.26%[/tex]
for such more questions on standard deviation
https://brainly.com/question/475676
#SPJ11
How do I solve this challenging math problem?
Answers
Answer:
13/32
Step-by-step explanation:
You want the area of the shaded portion of the unit square shown.
CircumcenterPoints B, C, E are shown as equidistant from point F, so will lie on a circle centered at F. The center of that circle is at the point of coincidence of the perpendicular bisectors of BE, BC, and CE.
Without loss of generality, we can let line EF lie on the x-axis such that E is at the origin. Chord EB of the circle has a rise of 1/2 for a run of 1, so a slope of 1/2. Its midpoint is (1, 1/2)/2 = (1/2, 1/4). The perpendicular line through this point will have slope -2, so its equation can be written ...
y -1/4 = -2(x -1/2)
y = -2x +5/4
Then the x-intercept (point F) will have coordinates (0, 5/8):
0 = -2x +5/4 . . . . . y=0 on the x-axis
2x = 5/4
x = 5/8
TrapezoidTrapezoid EFCD will have upper base 5/8, lower base 1, and height 1/2. Its area is ...
A = 1/2(b1 +b2)h
A = (1/2)(5/8 +1)(1/2) = (1/4)(13/8) = 13/32
The shaded area is 13/32.
__
Additional comment
The point-slope equation of a line through (h, k) with slope m is ...
y -k = m(x -h)
number 5 goes through the device and the result is 25 . what would a possible rule for machine B be ?
Answers
Answer: multiplied by 5 or squared
Step-by-step explanation:
If the number 5 goes in and 25 is the result, the rule could be multiplying by 5 or squaring the number that goes in (input).
5 x 5 = 25
5^2 = 25.
Find the value of x.
Answers
In the figure of circle provided. the value of x is
161 degreesHow to find the value of xIn a circle, equal chords subtends equal arc length.
In the problem it was given that:
chord SU is equal to chord ST hence we have that
x + x + 38 = 360 (angle in a circle)
collecting like terms
2x + 38 = 360
2x = 360 - 38
2x = 322
Isolating x by dividing both sides by 2
2x / 2 = 322 / 2
x = 161
Learn more about arc measures at:
https://brainly.com/question/30543683
#SPJ1
we learned in exercise 3.25 that about 69.7% of 18-20 year olds consumed alcoholic beverages in 2008. we now consider a random sample of fifty 18-20 year olds. a) how many people would you expect to have consumed alcoholic beverages? do not round your answer.
Answers
Rounding off the value of X to the nearest whole number, we get that approximately 35 people would be expected to have consumed alcoholic beverages among 50 randomly selected 18-20 year-olds.
In exercise 3.25, it was learned that about 69.7% of 18-20 year-olds consumed alcoholic beverages in 2008.
Now, consider a random sample of fifty 18-20 year-olds.
It is required to calculate the number of people who would be expected to have consumed alcoholic beverages.
Let X be the number of people who have consumed alcoholic beverages out of 50 randomly selected 18-20 year-olds.
Let p be the proportion of 18-20 year-olds who consumed alcoholic beverages in 2008.
Therefore, the sample proportion is given as \hat{p}
Hence, p=0.69 \hat{p}=X/50
Now, by the properties of the sample proportion, E(\hat{p})=p
Therefore,
E(\hat{p})=E(X/50)
Thus, p=E(X/50) Or, X=50p
Substituting the value of p, we have
X=50(0.697)=34.85
For similar question on approximately.
https://brainly.com/question/26355510
#SPJ11
if 10 friends are going to occupy 10 seats in shuttle on the way to the airport, how many different ways can they arrange themselves in the shuttle? provide your answer below:
Answers
If 10 friends are going to occupy 10 seats in a shuttle on the way to the airport, then they can arrange themselves in the shuttle in 10! or 3,628,800 ways.
Step-by-step explanation: There are 10 friends and 10 seats to be occupied in a shuttle.
Therefore, the number of ways to arrange the 10 friends in 10 seats is given by 10! (10 factorial), which is calculated as follows: 10! = 10 x 9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1= 3,628,800
Therefore, 10 friends can arrange themselves in the shuttle in 3,628,800 ways.
To know more about seating arrangement problems: https://brainly.com/question/30983234
#SPJ11
give the number of total electron groups, the number of bonding groups, and the number of lone pairs for geometry (a). express your answer as integers separated by commas.
Answers
Hence, the answer is (4, 3, 1).In conclusion The answer provided above is concise and ng factually correct, and it addresses the question directly.
In order to determine the number of total electron groups, bondiroups, and lone pairs for geometry (a), we need to use the VSEPR theory. According to this theory, the electron groups around a central atom in a molecule will arrange themselves in a way that minimizes their repulsion. The total number of electron groups includes both the bonding and lone pairs of electrons.To determine the number of electron groups for geometry (a), we first need to determine the molecular geometry of the molecule.
From the given name, we can assume that geometry (a) is tetrahedral. In a tetrahedral molecule, there are four electron groups: three bonding groups and one lone pair. Therefore, the number of total electron groups for geometry (a) is four, the number of bonding groups is three, and the number of lone pairs is one.
for such more questions on VSEPR theory.
https://brainly.com/question/26498231
#SPJ11
why does the gcf of the variables of a polynomial have the least exponent of any variable term in the polynomial brainly
Answers
The GCF (Greatest Common Factor) of the variables of a polynomial has the least exponent of any variable term in the polynomial because it represents the largest factor that is common to all the terms in the polynomial.
To understand this better, consider a polynomial like 6x²y³ + 9x³y². The GCF of this polynomial would be 3x²y², which is the largest factor that can divide both terms evenly.
Notice that the exponent of each variable in the GCF is the smallest exponent among the corresponding variable terms in the polynomial.
This is because any factor that is common to all terms in the polynomial must be able to divide each term without leaving a remainder. Therefore, the exponent of each variable in the GCF must be less than or equal to the exponent of that variable in every term of the polynomial.
In summary, the GCF of the variables of a polynomial has the least exponent of any variable term in the polynomial because it represents the largest factor that can divide all terms in the polynomial evenly, and therefore, it must have the smallest exponent of each variable among all terms in the polynomial.
To know more about greatest common factor click on below link:
https://brainly.com/question/11221202#
#SPJ11
A penny is 19 mm wide. What is the area of the front side of the penny? Use 3.14 for π. Round to the nearest hundredth if necessary.
HELP ME QUICK PLEASE!
Answers
Given that,
A penny is 19 millimeters wide. The area of the face of the coin? Round to the nearest hundredth is ot be determined and π = 3.14
What is an area circle?
The area of the circle is given by the pie times square of the radius.
Area of circle = πr^2
here,
Area of the penny = π[d / 2]²
Substitute the values in the above equation,
Area of the penny = 3.14 [19 / 2]²
Area of the penny = 283.385
Thus, the required area of the penny is given as 283.385 square millimeters.
Answer:
≈283,39 mm^2
Step-by-step explanation:
The diameter is 19 mm, so the radius is half diameter (9,5 mm)
[tex]a = \pi \times {r}^{2} = 3.14 \times {9.5}^{2} = 3.14 \times 90.25 ≈ 283.39[/tex]
Which of the series in exercises 17–56 converge, and which diverge? use any method, and give reasons for your answers
Answers
The given series diverges to negative infinity as the terms cancel out, leaving only two terms at the beginning and end of the series.
To determine the convergence of the given series, we can use the telescoping series method.
Let's write out a few terms of the series to see if we can spot a pattern:
n=1: 1/2 - 3/4 = -1/4
n=2: 2/3 - 4/5 = -2/15
n=3: 3/4 - 5/6 = -1/8
n=4: 4/5 - 6/7 = -2/35
...
We can see that the terms of the series cancel out, leaving only two terms at the beginning and end of the series. Therefore, we can write the series as:
∑ (n/n+1 - n+2/n+3) = 1/2 - (n+2)/(n+3)
As n approaches infinity, the second term approaches 1, so the series diverges to negative infinity.
Therefore, the given series diverges.
To know more about converge and diverge series:
https://brainly.com/question/15415793
#SPJ4
_____The given question is incomplete, the complete question is given below:
Which of the series in exercises 17–56 converge, and which diverge? use any method, and give reasons for your answers
(∑ ∞ to n = 1) = (n/n+1 - n+2/n+3)
solve for x, using a tangent and secant line
Answers
Check the picture below.
[tex]x^2=(8+2)(2)\implies x^2=20\implies x=\sqrt{20}\implies x\approx 4.5[/tex]
The value of x is 4.5 rounded to the nearest tenth.
What is Tangent and Secant of a Circle?Tangent of a circle is defined as the line which passes through exactly one point on the circle.
Secant of a circle is the line which passes through two points on the circle.
Secant-Tangent Rule states that if a tangent and a secant are drawn to a circle from the same point outside the circle, then the square of the length of the tangent segment is equal to the product of the lengths of secant and the segment of secant outside the circle.
Using the theorem, we can say here that,
(8 + 2) 2 = x²
x² = 10 × 2
x² = 20
x = √20
x = 4.472 ≈ 4.5
Hence the value of x is 4.5.
Learn more about Tangent and Secant here :
https://brainly.com/question/15178974
#SPJ5
Find the surface area of the solid. Round your answer to the nearest tenth
if necessary.
Answers
Area of the solid composite shape with triangle and rectangle is =832cm².
Define area of composite shapes?The area of a composite shape can be determined by adding or subtracting its component pieces.
Hence, we can use two formulas:
Area of Composite Shape + Area of Composite Shape + Area of Basic Shape A (additive)
Basic Shape Area A, Basic Shape Area B, and Composite Shape Area (subtractive)
In the figure,
Dimensions of the triangle are height, h = 16cm and base, b = 12cm.
Area = 1/2 ×b ×h
= 1/2 × 16× 12
=96cm²
There are two triangles, so the total area = 96+ 96 = 192cm².
Now area of the rectangle = length × width
= 20 × 32
= 640cm².
Total area of the solid= 192 + 640 = 832cm².
To know more about area, visit:
https://brainly.com/question/16890298
#SPJ1