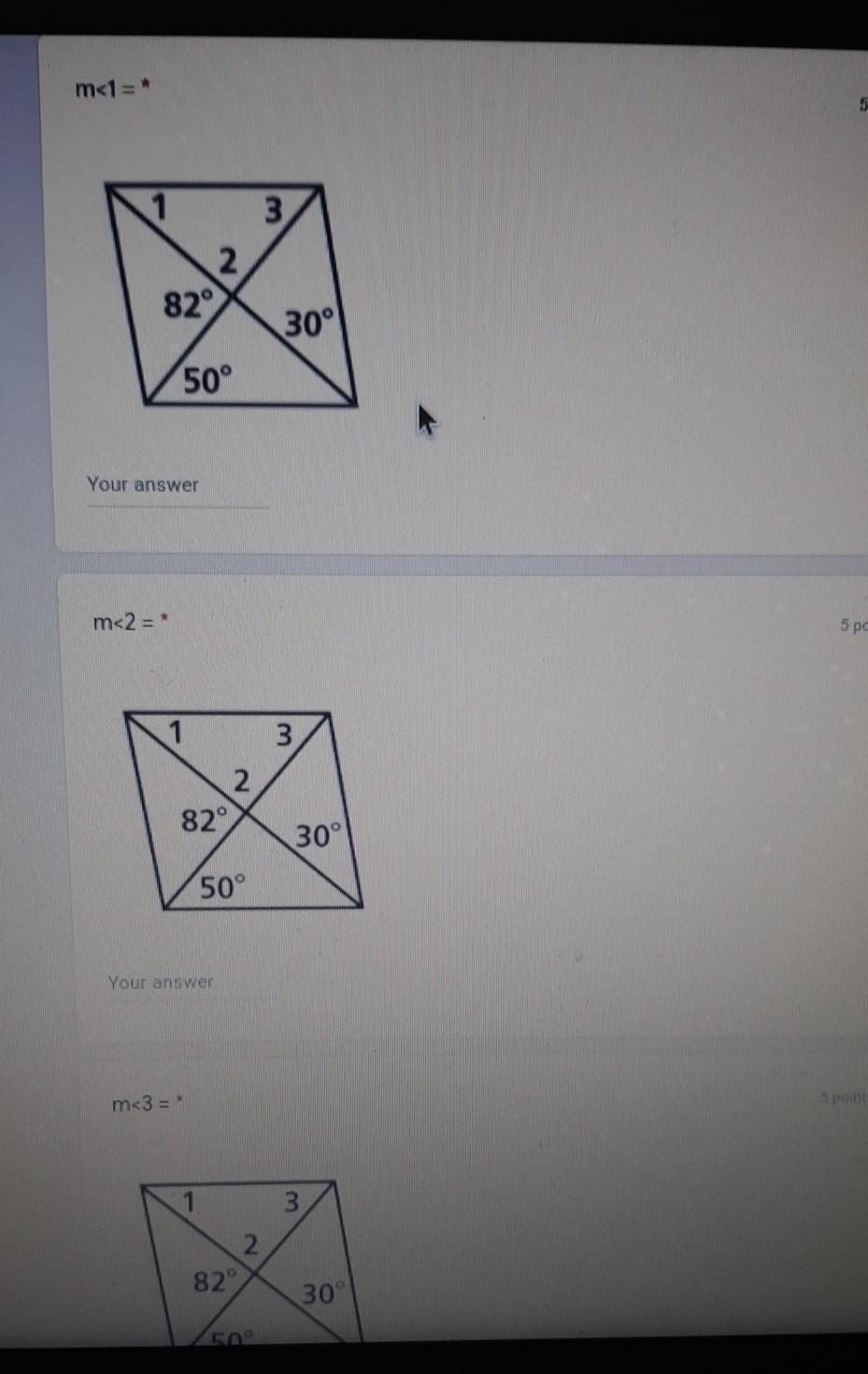
I know this is something super easy, but I always forget the steps on how to figure this out, I tried to put 30 and number one spot, I tried putting 82 and number two spot, and I tried putting 50 and number one spot but when you add that up that's a lot more than 360. I just need help please
Answers
Anlge directly opposite to 2= 180 - 82= 98
Sum of angles in the triangle (98, 50, x ) = 180
98+50+x = 180
x + 148 = 180
x = 180 - 148= 32
m<1 = x because they are alternate
so m<1 = 32
m<2 + 82 = 180 ( sum of angles in a straight line)
m<2 = 180 - 82 = 98
m< 3 = 50 because they are alternate
Or
m<3 + m<2 + m<1 = 180 ( sum of angles in a triangle)
m< 3 + 98+ 32 = 180
m<3 =180 - 130 =50
Summary
m< 1= 32 degrees
m<2= 98 degrees
m<3 = 50 degrees
Related Questions
I need help with his practice problems from my ACT prep guidePlease show your work in steps
Answers
Answer:
[tex]-\sqrt[]{6}+1[/tex]Explanation:
Given the below expression;
[tex]\frac{\tan(-\frac{2\pi}{3})}{\sin(\frac{7\pi}{4})}-\sec (-\pi)[/tex]Recall that;
[tex]\begin{gathered} \sec x=\frac{1}{\cos x} \\ \sin x=\cos (\frac{\pi}{2}-x) \end{gathered}[/tex]So we can rewrite the expression as;
[tex]\begin{gathered} \frac{\tan(-\frac{2\pi}{3})}{\cos(\pi-\frac{7\pi}{4})}-\frac{1}{\cos(-\pi)} \\ \frac{\tan(-\frac{2\pi}{3})}{\cos(-\frac{5\pi}{4})}-\frac{1}{\cos(-\pi)} \end{gathered}[/tex]Also, recall that;
[tex]\begin{gathered} \cos (-x)=\cos x \\ \tan (-x)=-\tan x \end{gathered}[/tex]So we'll have;
[tex]\frac{-\tan (\frac{2\pi}{3})}{\cos (\frac{5\pi}{4})}-\frac{1}{\cos (\pi)}[/tex]From the Unit circle, we have that;
[tex]\begin{gathered} \cos \pi=-1 \\ \cos (\frac{5\pi}{4})=\frac{-\sqrt[]{2}}{2} \\ \tan (\frac{2\pi}{3})=-\sqrt[]{3} \end{gathered}[/tex]Substituting the above values into the expression and simplifying, we'll have;
[tex]\begin{gathered} \frac{-(-\sqrt[]{3})}{\frac{-\sqrt[]{2}}{2}}-\frac{1}{-1}=\frac{\sqrt[]{3}}{\frac{-\sqrt[]{2}}{2}}+1=-\frac{2\sqrt[]{3}\sqrt[]{2}}{\sqrt[]{2}\cdot\sqrt[]{2}}+1 \\ =-\sqrt[]{6}+1 \end{gathered}[/tex]Check PictureGraph the polynomial given below by first selecting the number of points, then moving the points. You will need a point for each x intercept, and one for the y intercept.f(x)=17(x−1)(x+3)(x+7)
Answers
ANSWER
Graph:
EXPLANATION
Given:
[tex]f(x)\text{ = }\frac{1}{7}\left(x−1\right)\left(x+3\right)\left(x+7\right)[/tex]Desired Outcome:
Graph the polynomial
Plotting a few selected points using the table below
The local humane society is restocking on cat food to prepare for kitten season. Very young kittens need kitten formula which costs $4.00 per bottle. Older kittens need wet cat food which costs $1.50 per can. Answer numbers 5 and 6. 15) Write an algebraic expression to describe how much the humane society will spend on kitten supplies based on the number of bottles and the number of cans they buy. 16) How much money (before tax) will the humane society spend if they buy 5 bottles of kitten formula and 12 cans of wet cat food? Show your work.
Answers
Lets call B the nuber of bottles they will buy and C the number of cans.
Then, if each bottle cost $4, the cost of all the bottles will be 4B.
If each can cost $1.50, then, the total cost of the cans is 1.5C.
If we add this two costs, we have the expression we need:
[tex]\text{Cost}=4B+1.5C[/tex]If they buy 5 bottles of kitten formula and 12 cans of wet cat food, we have B=5 and C=12, and the cost is:
[tex]\text{Cost}=4B+1.5C=4\cdot5+1.5\cdot12=20+18=38[/tex]They will spend $38.
Divide the polynomial by the monomial (63xy^3+ 56x^2y^4)/(7xy)
Answers
ANSWER
9y² + 8xy³
EXPLANATION
To divide this polynomial by the given monomial, we can distribute the denominator into the sum,
[tex]\frac{63xy^3+56x^2y^4}{7xy}=\frac{63xy^3}{7xy}+\frac{56x^2y^4}{7xy}[/tex]Then, each coefficient simplifies with the coefficient of the monomial, since both are multiples of 7. Also, in the first term, x cancels out, and we have to subtract 1 from the exponent of y. In the second term, we subtract 1 from both the exponents of x and y,
[tex]\frac{63xy^3}{7xy}+\frac{56x^2y^4}{7xy}=9y^2+8xy^3[/tex]Hence, the result is 9y² + 8xy³.
Melissa works as a tutor for S12 an hour and as a waitress for S11 an hour. This month, she worked a combined total of 105 hoursat her two jobs.Lett be the number of hours Melissa worked as a tutor this month. Write an expression for the combined total dollar amount sheearned this month.
Answers
From the question
Melissa earns $12 an hour as a tutor
And $11 an hour as a waitress
Also,
This month, she worked a combined total of 105 hours
at her two jobs.
Let t be the number of hours Melissa worked as a tutor this month
Let w be the number of hours Melissa worked as a waitress this month
This implies
[tex]t+w=105[/tex]Since Melissa worked t hours as a tutor this month then
Total money earned as a tutor = $12t
Also,
Since Melissa worked w hours as a waitress this month then
Total money earned as a waitress this month = $11w
Therefore, the total combined earnings for the month is
[tex]\text{ \$12t }+\text{ \$11w}[/tex]What is the gcf of 16 and 28
Answers
Answer:
4
Step-by-step explanation:
Consider these functions:/(=) =-{=2 + 51g(I) = =2 + 2What is the value of fg(-2))?
Answers
Answer: Provided the two functions, f(x) and g(x), we have to find the composite of these two functions at x = - 2:
[tex]\begin{gathered} f(x)=-\frac{1}{2}x^2+5x \\ \\ g(x)=x^2+2 \end{gathered}[/tex]
The composite function is as follows:
[tex]\begin{gathered} f(g(x))=-\frac{1}{2}(x^2+2)^2+5(x^2+2) \\ \\ \\ f(g(x))=-\frac{1}{2}[x^4+4x^2+4]+5x^2+10 \\ \\ \\ f(g(x))=-\frac{x^4}{2}-2x^2-2+5x^2+10 \\ \\ f(g(x))=-\frac{x^4}{2}-2x^2-2+5x^2+10 \\ \\ \\ f(g(x))=-\frac{x^4}{2}+3x^2+8 \\ \\ \\ f(g(-2))=-\frac{(-2)^4}{2}+3(-2)^2+8 \\ \\ \\ f(g(-2))=-\frac{(-2)^4}{2}+3(-2)^2+8=-8+12+8=12 \\ \\ \\ f(g(-2))=12 \end{gathered}[/tex]The answer is 12.
$3.44 at the Farmers market at a grocery store the same oranges cost $8.40 for a bag of 20 find the better deal by calculating the unit rate for both locations how much would be saved per orange by purchasing oranges at the locations with the better deal solve the word problemFarmers market unit rate --------------grocery store unit rate ------------------better deal -------------how much is saved ------------A $0.01/ orangeslB $0.41 / orangeC grocery storeD Farmers marketE $0.43 / orangeF $0.40 / OrangeG $0.10 / Orange
Answers
Given :
At the farmer market : a bag of 8 oranges cost $3.44
At the grocery store : a bag of 20 oranges cost $8.4
So, the unit rate at the farmer market = 3.44/8 = $0.43/ orange
And the unit rate at the grocery store = 8.4/20 = $0.42/ orange
So, the better deal is the grocery store
how much is saved ?
the saving = 0.43 - 0.42 = $0.01/ orange
a positive integer is nice if there is a positive integer with exactly four positive divisors (including and ) such that the sum of the four divisors is equal to . how many numbers in the set are nice?
Answers
Answer:
A positive integer with exactly four positive divisors (including and ) such that the sum of the four divisors is equal to The sum of four divisors is equal to 45360.
What is an integer?
Zero, a positive natural number, or an unsigned negative integer are all examples of integers. The inverses of the equivalent positive numbers, which are additive, are the negative numbers. The boldface Z or blackboard bold "Z" is frequently used in mathematical notation to represent a collection of numbers.
Step-by-step explanation:
We know That total No. of factors
=product of (prime no′s power+1)
If N is the number of different divisors:
N=(p1+1)⋅(p2+1)⋅⋅⋅(pn+1)
100= 2^2 × 5^2
=2×2×5×5= (1+1)(1+1)(4+1)(4+1)
Then the integer n= a1^p1⋅a2^p2⋅⋅⋅⋅an^pn
For the smallest value: p1=4,p2=4,p3=1,p4=1
Then,
n=a1^4×a2^4×a3^1×a4^1
=24⋅34⋅51⋅71
=16⋅81⋅5⋅7
=45360
Hence, the positive integer with exactly four positive divisors (including and ) such that the sum of the four divisors is equal to The sum of four divisors is equal to 45360.
To learn more about the integers from the given link
https://brainly.com/question/929808
#SPJ4
[tex]4\sqrt[3]{16} /2\sqrt[3]{2}[/tex]
Answers
The expression 4∛16/2∛2 has a value of 4when simplified
How to evaluate the expression?From the question, the expression is given as
4∛16/2∛2
From the above parameter, we can see that the factors of the expression uses the cube root symbol
This means that the expression is a radical expression
Next, we have
4∛16/2∛2 = 4∛16/2∛2
Divide 4 by 2 in the equation
So, we have
4∛16/2∛2 = 2∛16/∛2
Solving further, we combine the cube roots (or radicals)
This is represented as
4∛16/2∛2 = 2∛(16/2)
Evaluate the quotient of 16 and 2
So, we have the following equation
4∛16/2∛2 = 2∛8
Take the cube root of 8
4∛16/2∛2 = 2 x 2
Evaluate the product
4∛16/2∛2 = 4
The expression cannot be further simplified
Hence, the solution to the expression 4∛16/2∛2 is 4
Read more about expression at
https://brainly.com/question/723406
#SPJ1
Find the average rate of change of f(x)=x2−x+2 on the interval [1,t].
Answers
The average rate of change of the function x²-x+2 on the interval [1,t] is t .
The Average Rate Of Change of the function g(x) on the interval [a,b] is given by the formula
Average rate of change = (g(b)-g(a))/(b-a) .
the function is given as x²-x+2
interval is given as [1,t] .
so a=1 and b=t .
f(a) = f(1) = 1²-1+2 = 1-1+2 = 2
f(b) = f(t) = t²-t+2
and , b-a = t-1
Substituting the values in the average rate of change formula , we get
Average rate of change = (t²-t+2-2)/(t-1)
= (t²-t)/(t-1)
taking t common from the numerator , we get
= t(t-1)/(t-1)
= t .
Therefore , the average rate of change of function x²-x+2 on the interval [1,t] is t .
Learn more about Average Rate Of Change here
https://brainly.com/question/21405235
#SPJ1
Calculate the value of each expression.
1) (-5)
/
4
2) (-5)-(-/-)
3)-20
4)-20
(-20)
(4)
5)
Answers
Answer:
1) -15/4 or -3.75
2) 15/4 or 3.75
3) 5
4) -5
5) -5
Step-by-step explanation:
Discuss the order of operations to explain why the expressions [(12÷(2+ 2)] ^3 and (12 ÷ 2) + 2^3 do not havethe same value.
Answers
The order of operations are different. Hence, the answers are not equal
Explanation:
Oder of operations using PEMDAS (Parenthesis, Exponent, Multiplication, Division, Addition, Subtraction)
[(12÷(2 + 2)]³ and (12 ÷ 2) + 2³
we solve seperately:
[(12÷(2+ 2)]³
we solve the parenthesis first:
(12 ÷ 4)³
then we apply division:
= (3)³
Then expand the exponent:
= 27
(12 ÷ 2) + 2³
we solve the parenthesis first:
6 + 2³
we expand the exponent:
6 + 8
we apply addition:
14
The order of operations are differnt. Hence, the answers are not equal
What is the solution to x^2 – 9x < –8?A. x < 1 or x > 8B. x < –8 or x > 1C. 1 < x < 8D. –8 < x < 1
Answers
INFORMATION:
We have the next inequality
[tex]x^2-9x<-8[/tex]And we must find its solution
STEP BY STEP EXPLANATION:
To solve it, we must:
1. Move all terms aside
[tex]x^2-9x+8<0[/tex]2. Factor x^2-9x+8
[tex](x-8)(x-1)<0[/tex]3. Solve for x
[tex]x=8\text{ or }x=1[/tex]4. From the values of x, we have these 3 intervals to test
[tex]\begin{gathered} x<1 \\ 18 \end{gathered}[/tex]5. Choose a test point for each interval
For the interval x < 1:
[tex]\begin{gathered} \text{ Using x }=0, \\ 0^2-9(0)<-8 \\ 0<-8 \end{gathered}[/tex]which is false. So, the interval is discarded.
For the interval 1 < x < 8:
[tex]\begin{gathered} \text{ Using x }=2, \\ 2^2-9(2)<-8 \\ -14<-8 \end{gathered}[/tex]which is true. So, the interval is maintained
For the interval x > 8:
[tex]\begin{gathered} \text{ Using x = 9,} \\ 9^2-9(9)<-8 \\ 0<-8 \end{gathered}[/tex]which is false. So, the interval is discarded.
Finally, the solution would be the interval that was maintained: 1 < x < 8.
ANSWER:
C. 1 < x < 8
Answer:
C. 1 < x < 8
Step-by-step explanation:
x² - 9x < -8
we will suppose some values for x to check which values will satisfy this inequality:
for x = 1
1(1-9) < -8 which is wrong
for x = 2
2(2-9) < -8 this is satisfying the inequality
for x = 8
8(8-9) < -8 which is wrong
let's take any negative value now,
let x = -2
-2(-2-9) < -8 which is wrong
thus x is the positive value which will always be greater than 1 and less than 8 for the given inequality.
a museum wants to use equal rows to arrange the African baskets. which list shows all the different possible arrangements so that all the rows have the same number. Assume that an arrangement such as 4 x 20 is the same as 20 x 4.
Answers
Answer:
(B)1 x 80,2x 40,4 x 20,5 x 16,8 x 10
Explanation:
The number of African Baskets = 80
The list of all possible arrangements so that all the rows have the same number will be a list that contains all the positive product of factors of 80.
Factors of 80 are: 1,2,4,5,8, 10, 16,20,40,80
The list is, therefore:
[tex]1\times80,2\times40,4\times20,5\times16,8\times10[/tex]The correct choice is B.
The dimensions of a cuboid are in the ratio 1:2:3 and its total surface area is 88m^s. Find the dimensions.
Answers
SOLUTION
Given the question in the question tab, the following are the solution steps to answer the question.
STEP 1: Write the formula for total surface area of cuboid
[tex]\begin{gathered} 2(lb+bh+lh) \\ \text{where l is the length} \\ b\text{ is the breadth} \\ \text{h is the height} \end{gathered}[/tex]STEP 2: Get the dimension of the sides
[tex]\begin{gathered} \text{ Since the dimensions of the cuboid are in the ratio 1:2:3} \\ the\text{ dimensions are given as:} \\ x,2x\text{ and }3x \\ \text{lenght}=x \\ \text{breadth}=2x \\ \text{height}=3x \end{gathered}[/tex]STEP 3: Substitute the dimensions into the formula to get the value of x
[tex]\begin{gathered} 2(lb+bh+lh)=88 \\ By\text{ substitution,} \\ 2((x\cdot2x)+(2x\cdot3x)+(x\cdot3x))=88 \\ \Rightarrow2(2x^2+6x^2+3x^2)=88 \\ \text{Divide both sides by 2} \\ \Rightarrow\frac{2(2x^2+6x^2+3x^2)}{2}=\frac{88}{2} \\ \Rightarrow2x^2+6x^2+3x^2=44 \\ 11x^2=44 \\ \text{Divide both sides by 11} \\ \frac{11x^2}{11}=\frac{44}{11} \\ x^2=4 \\ x=\sqrt[]{4}=2 \\ x=2m \end{gathered}[/tex]STEP 4: Get the other dimensions
[tex]\begin{gathered} \text{breadth}=2x \\ \text{substitute 2 for x} \\ \text{breadth}=2(2)m=4m \\ \\ To\text{ get height} \\ \text{height}=3x \\ \text{substitute 2 for x} \\ \text{height}=3(2)m=6m \end{gathered}[/tex]Hence, the dimensions are:
[tex]2m,4m,6m[/tex]Find the zeros of the following logarithmic function: f(x) = 2logx - 6.
Answers
You are redecorating your room and the only thing left to paint is your door. You're onlygoing to paint the side that faces the inside of your room. The door is 6 feet 10 inchestall and 30 inches wide. You need to know the surface area of the side of the door todetermine how much paint to buy. The hardware store sells paint by how much coversa square foot. What is the surface area of the garage door? Round your answer to thenearest square foot. (Hint: 1 square foot = 144 square inches) (gridded response)
Answers
The roblem tells us that a door needs to be painted on only one side that measures 6 ft and 10 in height by 30 in wide.
We need to find the area to be painted in order to buy the appropriate quantity of paint. The answer has to be given in square feet at the end.
We start by recalling that the door is represented by a rectangle, and the area of such is given by the height times the wid
which functions are inverses of each other?A. both pair 1 and pair 2B. pair 1 only C. Pair 2 only D. neither pair 1 nor pair 2
Answers
Answer:
The pair one functions are given below as
[tex]\begin{gathered} f(x)=2x-6,g(x)=\frac{x}{2}+3 \\ f(g(x))=2(\frac{x}{2}+3)-6 \\ g(f(x))=\frac{2x-6}{2}+3 \end{gathered}[/tex]Step 1:
From pair 1, substitute the value of x=1 in the
[tex]\begin{gathered} f(x)=2x-6, \\ f(1)=2(1)-6 \\ f(1)=2-6 \\ f(1)=-4 \\ \\ g(x)=\frac{x}{2}+3 \\ g(-4)=-\frac{4}{2}+3 \\ g(-4)=-2+3 \\ g(-4)=1 \end{gathered}[/tex]Step 2:
For pair 2, substitute x=1
[tex]f(x)=7x,g(x)=-7x[/tex][tex]\begin{gathered} f(x)=7x \\ f(1)=7(1) \\ f(1)=7 \\ \\ g(x)=-7x \\ g(7)=-7(7) \\ g(7)=-49 \end{gathered}[/tex]Step 3:
From pair one,
[tex]f(1)=-4,g(-4)=1[/tex]From pair 2,
[tex]f(1)=7,g(7)=-49[/tex][tex]f(x)=y,g(y)=x(\text{inverse)}[/tex]From the above conclusion, we can say that
The final answer is
PAIR 1 ONLY
OPTION B is the right answer
a polynomial function has four turning points and two zeros. it’s degree could be ___? select all that apply 4567
Answers
SOLUTION
A polynomial function with real coefficients has four turning points and two zeros could be a degree 6 or any higher even degree because a polynomial with degree n has at most (n - 1) turning points.
So, it cannot be a degree 4.
It cannot be a degree 5 because it has two real zeros, and then three complex roots. A polynomial function with real coefficients cannot have an odd number of complex roots.
Answer:
6
Step-by-step explanation:
edge 23
Write the phrase "8 more than 10 divided by x is 12" as a variable expression:
Answers
Answer:
10/x + 8 = 12
Step-by-step explanation:
10 divided by x = 10/x
8 more than 10 divided by x = 10/x + 8
How to solve problem 31? Solve for x y and z using ratios
Answers
The Solution:
Given:
Required:
Find the values for x, y, and z.
By the Similarity Theorem:
[tex]\Delta BAD\cong\Delta CBD[/tex]So,
[tex]\begin{gathered} \frac{x}{36}=\frac{36}{6x} \\ \\ \frac{x}{36}=\frac{6}{x} \end{gathered}[/tex]Cross multiply:
[tex]\begin{gathered} x^2=36\times6 \\ \\ x=\sqrt{36\times6}=6\sqrt{6} \end{gathered}[/tex]Find y by applying the Pythagorean Theorem on the right triangle CBD:
[tex]\begin{gathered} y^2=36^2+(6\sqrt{6)}^2 \\ \\ y=6\sqrt{42} \end{gathered}[/tex]Find z:
By the Pythagorean Theorem:
[tex]\begin{gathered} z^2=(42\sqrt{6})^2-(6\sqrt{42})^2 \\ \\ z=36\sqrt{7} \end{gathered}[/tex]Answer:
[tex]\begin{gathered} x=6\sqrt{6} \\ \\ y=6\sqrt{42} \\ \\ z=36\sqrt{7} \end{gathered}[/tex]solve the equation 3x^2 - 5x + 1 = 0 expressing your answer correct to two decimal places
Answers
You have th following equation;
[tex]3x^2-5x+1=0[/tex]In order to find the solution to the previous equation, use the quadratic formula:
[tex]x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}[/tex]In this case, a = 3, b = -5 and c = 1. By replacing these values into the quadratic formula, you obtain:
[tex]\begin{gathered} x=\frac{-(-5)\pm\sqrt[]{(-5)^2-4(3)(1)}}{2(1)} \\ x=\frac{5\pm\sqrt[]{25-12}}{2}=\frac{5\pm\sqrt[]{13}}{2} \\ x=\frac{5\pm3.60}{2}=2.5\pm1.80 \end{gathered}[/tex]Hence, the solutions are:
x = 2.5 + 1.80 = 4.30
x = 2.5 - 1.80 = 0.70
the difference between the number c and the quotient of a and b in a mathematical expression.
Answers
Answer:
no difference
step by step explanations
because a/b=c
these means c(b) and a(1)
cb=a this means
cb/b=a/b
b cancle by b
and c=a/b
what is the volume of a pipe that has a diameter of 8 meters and a height of 3 meters of water, round to the nearest tenth
Answers
The pipe is in the form of cylinder.
[tex]\begin{gathered} d\text{ = 8 m} \\ r\text{ = 4 m} \\ h\text{ = 3 m} \end{gathered}[/tex]The volume of the pipe is calculated as,
[tex]\begin{gathered} \text{Volume = }\pi\times r^2\times h \\ \text{Volume = 3.14 }\times\text{ 4}\times4\times3 \\ \text{Volume = 150.72 }\approx150.70m^3 \end{gathered}[/tex]Thus the volume of water is 150.70 cubic m .
Consider the function, Find the zeros or x-intercepts of f(x).
Answers
To find the x-intercepts, equate the function with zero as follows:
[tex]\begin{gathered} f(x)=0 \\ -16x^2+25x+10=0 \\ x=\frac{-25\pm\sqrt[]{(25)^2-4\times10\times-16}}{2\times-16} \\ x=\frac{-25\pm\sqrt[]{625+640}}{-32} \\ x=\frac{-25\pm35.5668}{-32} \\ x=-0.3302,1.8927 \end{gathered}[/tex]Hence the intercepts are -0.3302 and 1.8927
The intercepts are at points (-0.3302,0) and (1.8927,0)
the product of a number and 3, increased by 5, is 7 less than twice the number. write an equation
Answers
Answer:
[tex]3x + 5 = 2x - 7[/tex]
Question 7, pre calc, include the answer in bold please. I have bad WiFi so please finish question if I get disconnected so I can see it, thanks
Answers
Given the following function
[tex]f(x)=x^4-x^3+7x^2-9x-18[/tex]We want to find its roots. Since we already know that (x + 1) and (x - 2) are factors of this polynomial, we can divide our polynomial by those factors and factorize the result to get the other roots.
Let's start by dividing by the first factor
[tex]\frac{x^4-x^3+7x^2-9x-18}{x+1}[/tex]To divide a polynomial by other, we start by dividing the leading term of the dividend by the leading term of the divisor(this will be the first term of our result)
[tex]\frac{x^4}{x}=x^3[/tex]Then, we ultiply it by the divisor
[tex]x^3(x+1)=x^4+x^3[/tex]Subtracting this result from the dividend, we have
[tex](x^4-x^3+7x^2-9x-18)-(x^4+x^3)=-2x^3+7x^2-9x-18[/tex]This means that our division is
[tex]\frac{x^4-x^3+7x^2-9x-18}{x+1}=x^3+\frac{-2x^3+7x^2-9x-18}{x+1}[/tex]Repeating the whole process of division with the second term, we have
[tex]\begin{gathered} x^3+\frac{-2x^3+7x^2-9x-18}{x+1}=x^3-2x^2+\frac{9x^2-9x-18}{x+1} \\ \Rightarrow\frac{x^4-x^3+7x^2-9x-18}{x+1}=x^3-2x^2+9x-18 \end{gathered}[/tex]From this result, we can rewrite our function as
[tex]x^4-x^3+7x^2-9x-18=(x+1)(x^3-2x^2+9x-18)[/tex]Repeating this same process with the other know factor, the other division we have to solve is
[tex]\frac{(x^3-2x^2+9x-18)}{x-2}=x^2+9[/tex]Then, our function is
[tex]f(x)=(x^4-x^3+7x^2-9x-18)=(x+1)(x-2)(x^2+9)[/tex]Then, to find the roots we need to solve the following equation
[tex](x+1)(x-2)(x^2+9)=0[/tex]Since we have a product of 3 terms, the result will be zero if and only if one of the terms is zero. This means that the roots can be found by assuming each one is zero. The solutions for this equation are the same solutions for the following system
[tex]\begin{cases}x+1=0 \\ x-2=0 \\ x^2+9=0\end{cases}\Rightarrow\begin{cases}x=-1 \\ x=2 \\ x=\pm\sqrt[]{-9}=\pm3i\end{cases}[/tex]And those are the roots for our function. x = -1, 2, +-3i.
1.) You are buying flower bundles and have
$24 to spend. Rose bundles cost $4. Tulip bundles
cost $6. Write an equation to describe how many
types of each kind of bundle you can buy.
Answers
Answer:
[tex]4r+6t \leq 24[/tex]
Step-by-step explanation:
The cost of money spent on a rose bundle can be represented by 4r, where 4 is the cost of one rose bundle and r is the number of rose bundles purchased.
The cost of money spent on a tulip bundle can be represented by 6t, where 6 is the cost of one tulip bundle and t is the number of rose bundles purchased.
The amount spent on rose bundles added to the amount spent on tulip bundles must be equal to or less than $24, since that's all you have to spend. This can be represented using this equation:
[tex]4r + 6t \leq 24[/tex]
:)
Which relation below is not a function
Answers
Answer:
0,0
Step-by-step explanation:
Two numbers can not equal another number