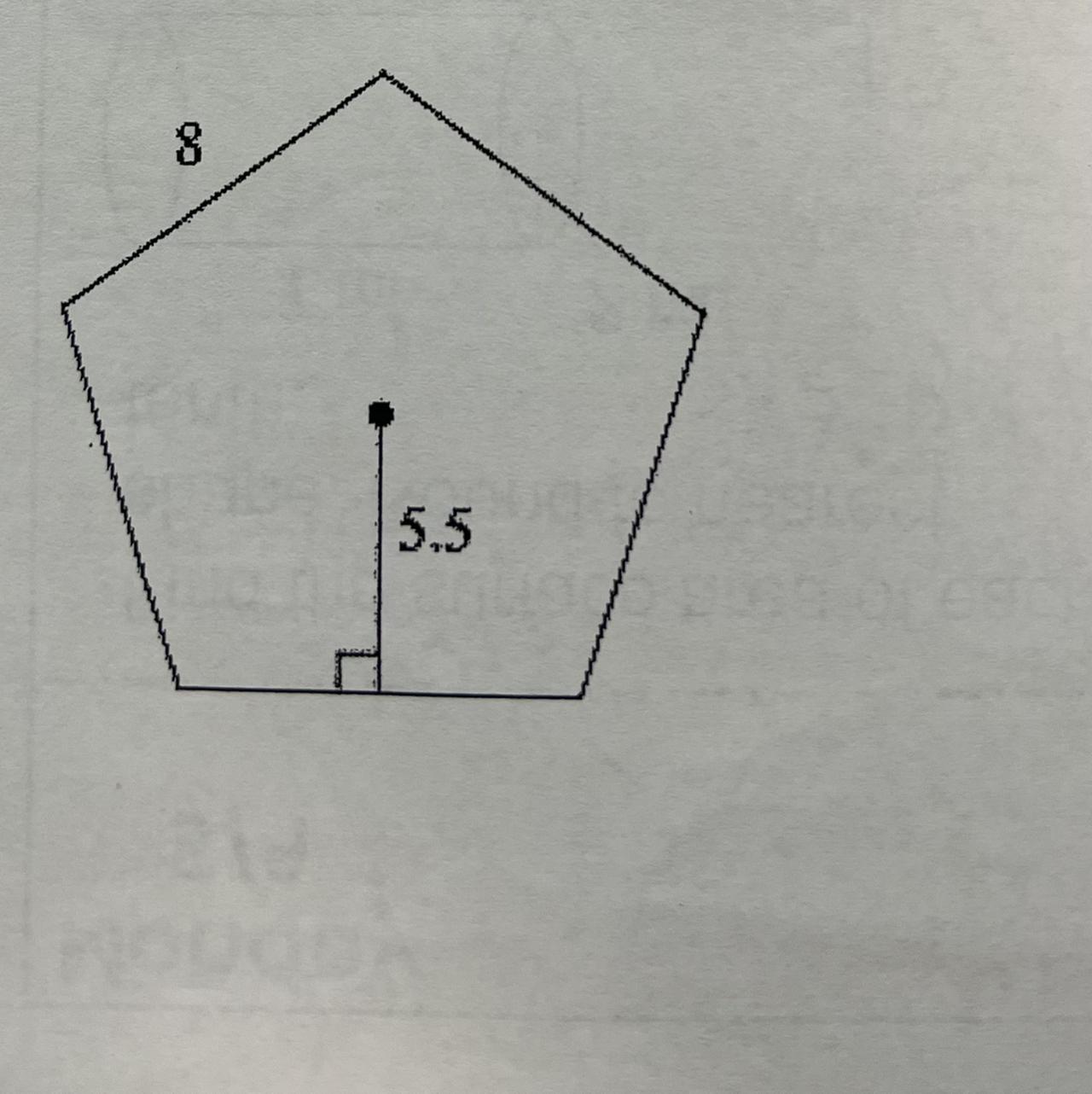
I need help with the work question Find area of regular polygon.Round to nearest tenth
Answers
Given:
The number of sides in a given polygon is n = 5.
The length of each side is s = 8
The length of the apothem is a = 5.5
To find:
The area of the regular polygon
Explanation:
The formula of the area of the regular polygon is,
[tex]\begin{gathered} A=\frac{1}{2}\times n\times s\times a \\ A=\frac{1}{2}\times5\times8\times5.5 \\ A=110\text{ units}^2 \end{gathered}[/tex]Thus, the area of the given regular polygon is 110 square units.
Final answer:
The area of the regular polygon is 110 square units.
Related Questions
Floyd is an aspiring music artist. He has arecord contract that pays him a base rate of$200 a month and an additional $12 for eachalbum that he sells. Last month he earned atotal of $644.Write an equation to determine the numberof albums (a) Floyd sold last month.Find the number of albums Floyd sold lastmonth.albums
Answers
Explanation:
Equate the given data to solve for x.
$200 + $12x = $644.
To determine the number of albums sold, Let x be the number of album sold by Floyd last month.
200 + 12x = 644
12x =644-200
12x = 444
x = 444/12
x= 37.
Floyd has sold 37 albums last month.
Answer:
The equation to determine the number of albums Floyd sold last month is 200+12x = 644.
and the number of album Floyd sold last month is 37.
Use the triangle to answer the question.Find the sine of angle Y.
Answers
In a right triangle, given an angle, the ratio between the opposite side of this angle by the hypotenuse is equal to the sine of the angle. Using this relation in our triangle, we have
[tex]\sin Y=\frac{6}{10}=\frac{3}{5}[/tex]Please help me solve this using six grade math (easy formulas)
Answers
We will break the surface area of the tent up into its sides, the front and the back and the bottom.
Area of the sides: 2(5*7) = 70
Area of the front and the back: 2( 1/2 (6*4)) = 24
Area of the bottom: 7*6 = 42
Least amount of fabric required = 136ft
Im in algebra 2 but we are also learning geometry the question asks to find the length of each arc
Answers
The length of the arc = 8π/3 mi
Explanation:The length of an arc is given by the fomula:
[tex]L=\frac{\theta}{360}\times2\pi r[/tex]The radius, r = 8 ml
[tex]\theta=60^0[/tex][tex]\begin{gathered} L=\frac{60}{360}\times2\pi\times8 \\ \\ L=\frac{16\pi}{6} \\ \\ L=\frac{8\pi}{3} \end{gathered}[/tex]The length of the arc = 8π/3 mi
Find the cube roots of 4−6i4−6iShow all your work.Include an explanation and diagram showing how DeMoivre's Theorem helps to solve this problem.
Answers
Given the following complex number
[tex]z=4-6i[/tex]We will find the cube root of the complex number using the following formula:
[tex]^3\sqrt{z}=\sqrt[3]{|z|}*(cos\text{ }\frac{\theta+2\pi k}{3}+i*sin\text{ }\frac{\theta+2\pi k}{3})[/tex]The formula is called De Moivre's theorem of the nth root
We have substituted n = 3
So, first, we will convert the given number from the rectangular form to the polar form
[tex]\begin{gathered} |z|=\sqrt{4^2+6^2}\approx7.211 \\ \theta=tan^{-1}\frac{-6}{4}=303.7\degree \end{gathered}[/tex]Substitute the magnitude and the angle and k = 0, 1, 2
So, there are 3 cubic roots of the given number as follows:
[tex]\begin{gathered} k=0\rightarrow z_1=\sqrt[3]{7.211}(cos\frac{303.7}{3}+i*sin\frac{303.7}{3})=1.932(cos101.23+i*sin101.23) \\ \\ k=1\rightarrow z_2=\sqrt[3]{7.211}(cos\frac{303.7+2\pi}{3}+i*sin\frac{303.7+2\pi}{3})=1.932(cos221.23+i*sin221.23) \\ \\ k=2\rightarrow z_3=\sqrt[3]{7.211}(cos\frac{303.7+4\pi}{3}+i*sin\frac{303.7+4\pi}{3})=1.932(cos341.23+i*sin341.23) \end{gathered}[/tex]Kacie is constructing the inscribed circle for △MNP. She constructed the angle bisectors of angle M and angle N and labeled the intersection of the bisectors as point A.Which construction is a correct next step for Kacie?Open the compass to the width of AM¯¯¯¯¯¯ and draw a circle centered at point A.Open the compass to the width of , A M ¯ , and draw a circle centered at point , A, .Construct the perpendicular bisector of AM¯¯¯¯¯¯ .Construct the perpendicular bisector of , A M ¯ , .Open the compass to the width of AP¯¯¯¯¯ and draw a circle centered at point A.Open the compass to the width of , A P ¯ , and draw a circle centered at point , A, .Construct the line that passes through point A and is perpendicular to NP¯¯¯¯¯¯ .
Answers
From the statement, we know that:
• Kacie is constructing the inscribed circle for △MNP,
,• she constructed the angle bisectors of angle M and angle N,
• and labelled the intersection of the bisectors as point A.
(1) Now, Kacy must construct a perpendicular from the centre point to one side of the triangle.
(2) After this, she must place the compass on the centre point while adjusting its length to the point where the perpendicular crosses the triangle.
(3) Finally, she must draw the inscribed circle.
So the answer is that Kacy must construct the perpendicular bisector of AM.
AnswerConstruct the perpendicular bisector of AM
Michael and his sister Mel share the job of mowing the grass in their yard. Michael mows ⅓ of the yard, and Mel mows the rest. Mel can mow ¾ of the entire yard in an hour.How long will it take Mel to finish mowing the yard?? Also after Michael mows 1/3 of the yard what fraction of the yard does mel need to mow?
Answers
Michael Mows = 1/3 of the yard
Mel mows the rest = 1-1/3 = 2/3 of the yard
Mel mows = 3/4 of the yard in an hour
After Michael mows 1/3 of the yard what fraction of the yard does Mel need to mow?
1- 1/3 = 2/3 of the yard
How long will it take Mel to finish mowing the yard??
2/3 / (3/4) = 8/9 hours = 0.89 hours
AMNP ~ AQRP N x + 8 28 M 24 P 3x - 9 R Create a proportion and find the length of side PR*
Answers
Using thales theorem:
[tex]\begin{gathered} \frac{24}{28}=\frac{x+8}{3x-9} \\ 24(3x-9)=28(x+8) \\ 72x-216=28x+224 \\ 44x=440 \\ x=\frac{440}{44} \\ x=10 \\ PR=3(10)-9=21 \end{gathered}[/tex]suppose that the time required to complete a 1040r tax form is normally distributed with a mean of 100 minutes and a standard deviation of 15 minutes. what proportion of 1040r tax forms will be completed in less than 77 minutes? round your answer to at least four decimal places.
Answers
The proportion of 1040r tax forms completed in less than 77 minutes = 0.06301
How to find the proportion of the tax forms?
The time required to complete a 1040r tax form = normally distributed
Mean = [tex]\mu[/tex] = 100 minutes
Standard deviation = [tex]\sigma[/tex] = 15 minutes
The proportion of 1040r tax forms completed in less than 77 minutes is given by ,
P( X< 77 ) = P ( Z < [tex]\frac{77-100}{15}[/tex] )
= P( Z < - 1.53 )
=0.06301
Cumulative probability in the normal distribution =0.06301 or 6.301%
What is normal distribution?
A probability distribution that is symmetric about the mean is the normal distribution, sometimes referred to as the Gaussian distribution.It demonstrates that data that are close to the mean occur more frequently than data that are far from the mean.The natural and social sciences frequently utilize normal distributions to describe real-valued random variables whose distributions are unknown, which is why normal distributions are essential in statistics. Not all symmetrical distributions are normal, but all normal distributions are symmetrical.Natural occurrences frequently resemble the normal distribution.A bell curve is another name for a normal distribution.To learn more about normal distribution, refer:
https://brainly.com/question/4079902
#SPJ4
Two airplanes are flying in the air at the same height. Airplane A is flying east at 451 mi/h and airplane B is flying north at 494 mi/h. If they are both heading to the same airport, located 3 miles east of airplane A and 3 miles north of airplane B, at what rate is the distance between the airplanes changing?
Answers
The rate at which the distance between the airplanes is changing is 668.2 mi/h.
In the given question,
Speed of Airplane A:
dA/dt = 451 mi/h
and the Speed of Airplane B:
dB/dt = 494 mi/h
Aircraft A and B will form a right triangle because Aircraft A is flying east and Aircraft B is flying north, and we can use Pythagoras' theorem to calculate their distance from one another.
Let P be the distance.
P² = A² + B²
Differentiating the above equation with respect to t,
2P(dP/dt) = 2A(dA/dt) + 2B(dB/dt)
Dividing each side of the equation by 2,
P( dP/dt ) = A( dA/dt ) + B( dB/dt ) ..........(1)
Where dP/dt is the rate of change in distance between the two aircraft.
Now,
P² = A² + B²
P = √(A² + B²)
Substituting, A = 3 miles and B = 3miles;
P = √(3² + 3²)
P = √( 9+ 9)
P = √18
P = 3√2 miles
Substituting the value in the equation (i)
3√2 (dP/dt) = (3× 451) + (3× 494)
3√2 (dP/dt) = 2835
4.2426 × dP/dt = 2835
dP/dt = 2835/4.2426
dP/dt = 668.2 mi/h
Therefore, the rate at which the distance between the airplanes is changing is 668.2 mi/h
Learn more about distance here:
brainly.com/question/15172156
#SPJ1
Slope The first two sets of points are 9,-24 and 13,-21
Answers
We need to find the slope using the points (9, -24) and (13 , -21)
so, the slope = 3/4
First drop down menu A. 2 B. 4 C. 8 Second drop down main choices A.30 B. 120 C. 60
Answers
SOLUTION:
Step 1:
In this question, we are given the following:
Step 2:
From the question, it takes 2 ounces of paint to completely cover all 6 sides of a rectangular prism box that holds 15 cups of sugar.
If we double the dimensions of the box,
it means that the scale factor will be 2.
Hence, the area factor will be:
[tex]2^2=\text{ 2 x 2 = 4}[/tex]Part A:
The new box would require 4 oz -- ( OPTION B)
of paint to cover with the paint.
Part B:
Given the scale factor is 2,
Then the area factor is 2 x 2 = 4,
Then the volume factor is 2 x 2 x 2 = 8 times
Recall that:
The rectangular prism box holds 15 cups of sugar,
Then the new box would hold ( 15 x 8 = 120 cups of sugar ) --OPTION B
7-Which beans are the better deal? Kidney Beans $1.18 per lb O Lima Beans $213 for 2 lbs 76-What is the Unit Price for the better deal? Round to the nearest hundredth) Put your answer in the form 0.00 or .00, so if answer is 43 cents, its 0.43 or.43, if there is a dollar amount like 1.50, do not add zeros in front).
Answers
Given :
Two kinds of Beans :
1. Kidney Beans $1.18 per lb
The unit price = $1.18
2. O Lima Beans $213 for 2 lbs
The unit price = 2.13/2 = 1.065
Rounding to the nearest hundredth
So,
The unit
In a right triangle, one of the acute angles measures of degrees. What is the measure of the other acute angle?
A. 90-d
B. 90 d
C. 180-d
D. 180+d
Answers
The correct answer is A. 90 - d
Since the sum of all the angles in a triangle is 180° and one of the angle is 90° because the triangle is a right triangle. So the sum of the remaining angles is 90°.
And to find the other acute angle we use 90° - d.
To learn more about angles in a triangle visit : brainly.com/question/27682397
Multiplying Polynomials 5y[tex] ({5y}^{2} + y + 3)(x - 2)[/tex]
Answers
Let's distribute those factors, and expand this:
[tex]\begin{gathered} (5y^2+y+3)\mleft(x-2\mright) \\ 5xy^2-10y^2+xy-2y+3x-6 \\ \end{gathered}[/tex]There's no further way beyond that. Either we pick the factored form or the expanded version of that polynomial. As this is not an equation we stop it here.
Been out of school for health issues trying to catch up work thanks!!
Answers
DEFINITIONS
The union of two sets contains all the elements contained in either set (or both sets). The union is notated A ⋃ B.
The intersection of two sets contains only the elements that are in both sets. The intersection is notated A ⋂ B.
Using a Venn Diagram, the union and intersection of two sets can be seen below:
GIVEN
The sets are given to be:
[tex]\begin{gathered} S=\mleft\lbrace1,2,3,\ldots,18,19,20\mright\rbrace \\ A=\mleft\lbrace3,4,8,9,11,13,14,15,20\mright\rbrace \\ B=\mleft\lbrace4,7,13,14,16,18,19\mright\rbrace \end{gathered}[/tex]QUESTION
1) (A ∪ B): The terms of the two sets contained in either set or the two sets are
[tex](A\cup B)=\mleft\lbrace3,4,7,8,9,11,13,14,15,16,18,19,20\mright\rbrace[/tex]2) (A ∩ B): The elements that are in both sets are
[tex](A\cap B)=\mleft\lbrace4,13,14\mright\rbrace[/tex]Mary estimates the weight of her cat to be 10 pounds.the actual weight of the cat is 13.75 pounds.find the percent error.
Answers
The percentage error is the ratio of the difference between the two readings and the actual
Error = 13.75 - 10
= 3.75
Percent error = 3.75/13.75
= 27.27%
1+1=? Need Help! Asap
Answers
By definition, Addition is a mathematical operation.
In this case, you have the following Addition given in the exercise:
[tex]1+1[/tex]Which is an equivalent expression for 4 times d raised
to the negative third power all over quantity 18 times d
raised to the ninth power end quantity?
Answers
Answer:
2d⁻³/9d⁻⁹
Step-by-step explanation:
4 times d raised to the negative third power = (4 × d)⁻³ = 4d⁻³
18 times d raised to the ninth power = (18 × d)⁻⁹ = 18d⁻⁹
the equation as a quotient:
Expression = 4d⁻³/18d⁻⁹
Expression = 2d⁻³/9d⁻⁹
Subtract these polynomials.
(3x + 2x + 4) (x + 2x+ 1) =
Answers
=(3x2 + 2x + 4) - (x2 + 2x + 1)
Combine like terms
=(3x2-x2)+(2x-2x)+(4-1)
=2x2+0+3
The 2x terms cancel each other to 0
=2x2+3
C) 2x2+3 is the answer.
Hope this helps!
Answer:
15x^2+17x+4
Step-by-step explanation:
(3x+2x+4)(x+2x+1)
Combine 3x and 2x to get 5x.
(5x+4)(x+2x+1)
Combine x and 2x to get 3x.
(5x+4)(3x+1)
Apply the distributive property by multiplying each term of 5x+4 by each term of 3x+1.
15x ^2+5x+12x+4
Combine 5x and 12x to get 17x.
15x^2+17x+4
Learn More: https://brainly.com/question/28956868
50% of $277 is $144True or False
Answers
Answer:
FALSE
Explanation:
Given the expression
50% of $277
This can also be written as;
= 50/100 * 277
= 1/2 * 277
= 277/2
= 138.5
Therefore 50% of $277 is $138.5 not $144 rendering the question FALSE
what is the x intercepts or zeros for y = x^2 - 6x + 5
Answers
Solution:
Given;
[tex]y=x^2-6x+5[/tex]The x-intercepts are the points where y=0.
Thus;
[tex]x^2-6x+5=0[/tex]Thus;
[tex]\begin{gathered} x^2-x-5x+5=0 \\ \\ x(x-1)-5(x-1)=0 \\ \\ x-1=0,x-5=0 \\ \\ x=1,x=5 \end{gathered}[/tex]ANSWER:
[tex]x=1,x=5[/tex]a sociology Professor assigns letter grades on a test according to the following scheme Scores on the test are normally distributed with the meaning of 67.2 and a standard deviation of 8.5Find the minimum score required for an a grade. Round your answer to the nearest whole number if necessary
Answers
In order to have grade A, the score needs to be in the top 9%.
Since the scores are normally distributed, the top 9% scores correspond to 91% of the area under the normal curve. That means we need to find a value of z in the z-table that corresponds to the value 0.91 (that is, 91%).
Looking at the z-table, the value of z for a probability of 0.91 is z = 1.34.
Now, to find the score that this value of z represents, we can use the formula below:
[tex]\begin{gathered} z=\frac{x-\mu}{\sigma}\\ \\ 1.34=\frac{x-67.2}{8.5}\\ \\ x-67.2=11.39\\ \\ x=11.39+67.2\\ \\ x=78.59 \end{gathered}[/tex]Rounding to the nearest whole number, the minimum score for grade A is 79.
Braden goes to the store to buy earmuffs. The sign says they were originally $13.50 but they are on sale for 15% off. What is the cost of the earmuffs now
Answers
Answer:
$11.48
Step-by-step explanation:
Change 15% to 0.15. then you multiply 13.50 by 0.15
13.50 x 0.15 = 2.025
Then you round 2.025
by rounding 2.025 you should get 2.03
with that you should subtract $13.50 by 2.03
13.50 - 2.03 = 11.48
I hope this helps :)
Solve pls. I neeeeeeeeed your help.
Answers
Answer:
70 over 39
Step-by-step explanation:
here's the solution first multiple the numbers with the fraction then calculate after that simply the fractions and the answer is
[tex] \frac{70}{39} [/tex]
Given a polyhedron with 6 vertices and 12 edges, how many faces does it have?
Answers
SOLUTION
GIVEN
A polyhedron has 6 vertices and 12 edges.
TO DETERMINE
The number of faces
CONCEPT TO BE IMPLEMENTED
Euler’s formula for Polyhedron :
For polyhedron F + V = E + 2
Where F stands for number of faces , V stands for number of vertices , E stands for number of edges .
EVALUATION
Here it is given that a polyhedron has 6 vertices and 12 edges
V = Number of vertices = 6
E = Number of edges = 12
F = Number of faces = ?
By Euler’s formula
F + V = E + 2
⇒ F + 6 = 12 + 2
⇒ F + 6 = 14
⇒ F = 8
FINAL ANSWER
The number of faces = 8
Writing the equation of a quadratic function given its graph
Answers
Answer:
[tex]y=-(x-1)^2+2[/tex]Step-by-step explanation:
A quadratic function in vertex form is represented as:
[tex]\begin{gathered} y=a(x-h)^2+k \\ \text{where,} \\ (h,k)\text{ is the vertex} \end{gathered}[/tex]Given the vertex (1,2) substitute it into the function:
[tex]y=a(x-1)^2+2[/tex]As you can see, we still do not know the value for ''a'', use the point given (4,-7) substitute it (x,y) and solve for ''a'':
[tex]\begin{gathered} -7=a(4-1)^2+2 \\ -7=a(3)^2+2 \\ -7=9a+2 \\ 9a=-7-2 \\ a=-\frac{9}{9} \\ a=-1 \end{gathered}[/tex]Hence, the equation of the function would be:
[tex]y=-(x-1)^2+2[/tex]Find the volume of the top of the prism, volume of the bottom prism, and total volume of figure.
Answers
Volume of the top of the prism: 460 cm^3
Volume of the bottom of the prism: 1 768 cm^3
Total volume of the figure: 2 228 cm^3
Explanation:
Volume of the top of the prism:
. Since it is a prism from trapezoid
. . Volume = Area of the trapezium base * heights between trapezium ends
[tex]\begin{gathered} Area\text{ of a trapezium base}=\frac{top\text{ base+bottom base}}{2}*height \\ ...\text{ =}\frac{6+17}{2}*(22-17) \\ ...=\frac{23}{2}*5 \\ Area\text{ = 57.5 cm}^2 \end{gathered}[/tex][tex]Volume=57.5*8=460\text{ }cm^3[/tex]Volume of the bottom prism:
. Since the price has a rectangular base:
Volume = Area of one base * height between reactangular bases
Area of one base :
[tex]17*13=221\text{ }cm^2[/tex]Volume:
[tex]221*8=1\text{ }768\text{ }cm^3[/tex]Total volume of the figure:
Volume of the top + Volume of the bottom = Total volume
[tex]221+1\text{ }768=2\text{ }228\text{ }cm^3[/tex]NB:
To find any volume of a given prism, start with finding the area of one base, then multiply that area by the height (in other words the sides that link the two bases)
while exploring a volcano zane heard somerumbling, so he decided to climb up out of there as quicklyas he could zane's elevation relative to the edge of the inside of the volcano (in meter) as a function time (in seconds) is graphed. PLEASE HELP ME WITH THIS How long did it take Zane to reach the edge of the volcano?
Answers
We have to find the time it took for Zane to be in the same elevation as the edge of the Volcano, that is, when his relative elevation is 0 on the graphic.
This happens at a time of 35 seconds. So:
It took Zane 35 seconds to reach the edge of the volcano.
Find the length of arc CD. Use 3.14for tt. Round to the nearest tenth.h 7.9 cm66.40D[? ]cm
Answers
For this problem we know that the radius is 7.9cm and the angle between C and D is 66.4ª. We also want to find the arclenght so we can use the following formula:
[tex]AL=\frac{x}{360}\cdot2\pi r[/tex]Where x is the angle and r the radius r=7.9cm. So then replacing into the function we got:
[tex]AL=\frac{66.4}{360}\cdot2\pi(7.9cm)=9.16\operatorname{cm}[/tex]And if we round to the nearest tenth we got 9.2 cm