Answers
Answer:
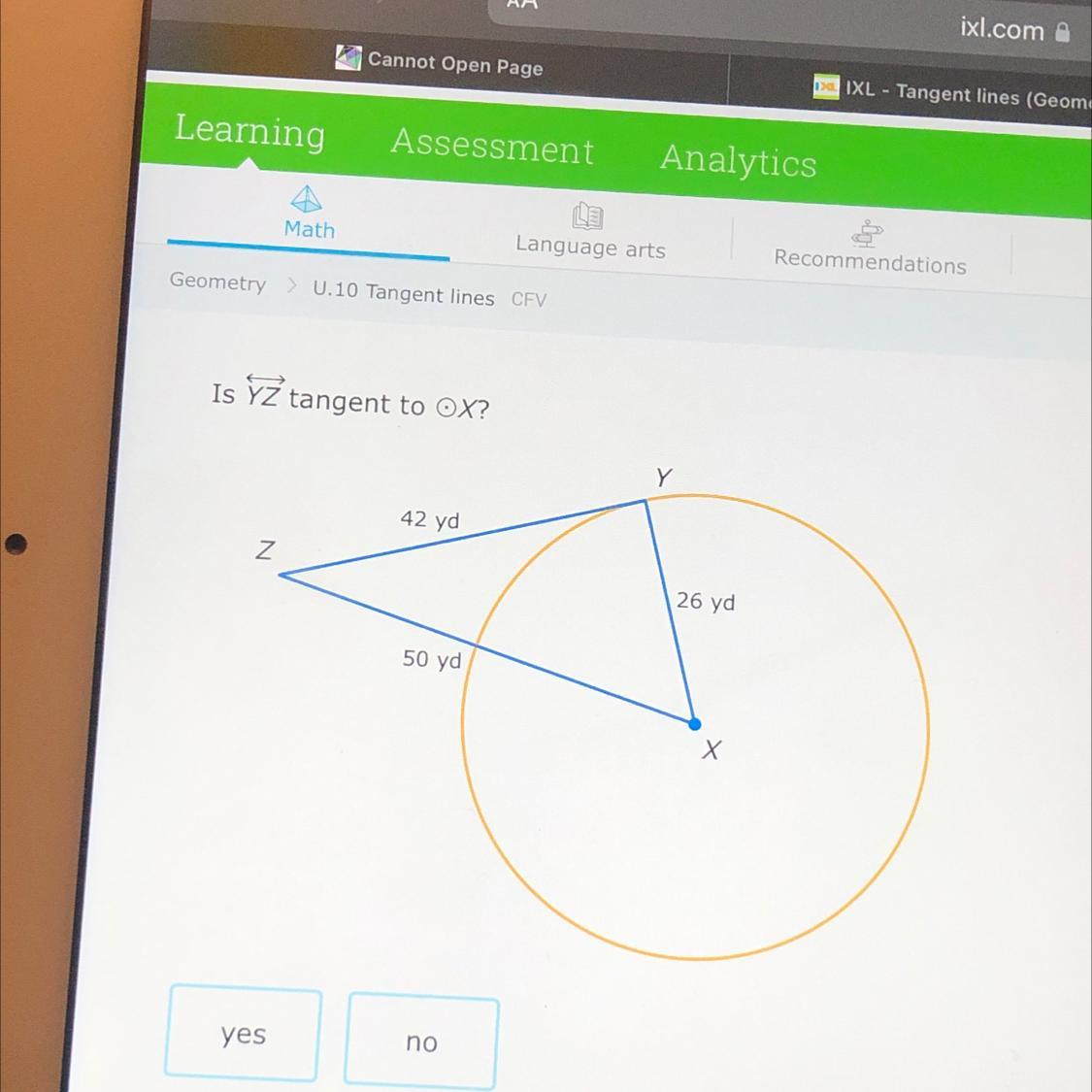
no
Step-by-step explanation:
using Pythagorean theorem:
[tex]26^{2} +42^{2}=50^{2}[/tex]
676+1764=2500
2440=2500
2440<2500
Answer:no
Related Questions
PACKAGING A video game system is packaged in a box that is in the shape of a cube. The length of the packaging box is 4x^2 y^5 . What is the volume of the packaging box in terms of x and y?
Answers
Answer: 64x^6y^15
Step-by-step explanation:
If the packaging box is in the shape of a cube, then all its sides are equal in length. Let's call the length of each side "s".
We know that the length of the packaging box is 4x^2 y^5, so:
s = 4x^2 y^5
To find the volume of the packaging box, we need to calculate s^3 (since the box is a cube).
s^3 = (4x^2 y^5)^3
s^3 = 4^3 (x^2)^3 (y^5)^3
s^3 = 64x^6 y^15
Therefore, the volume of the packaging box in terms of x and y is 64x^6 y^15.
Translate the figure 5 units left and 5 units up. -10-9 Plot all of the points of the translated figure. You may click a plotted point to delete it.
Answers
I hoped this helped!
: )
Step-by-step explanation:
originally - (6,-1) After translation - (1,4)
originally - (8,-1) After translation - (3,4)
originally - (4,-7) After translation - (-1,-2)
originally - (7,-9) After translation - (3,-4)
originally - (9,-9) After translation - (4,-4)
PLEASE HURRY !! I NEED HELP!!!
Answers
Answer:$10
Step-by-step explanation: We are given the ratio 9:1. Meaning for every 9 dollars he spends on healthy food, he can spend a dollar on snacks. If he intends on paying 100 dollars total, how much will he spend on snacks?
He would have spent 90 dollars on healthy food, and 10 dollars on snack food. Totaling 100 dollars.
A house plan has concrete stairs leading down into the garage. How much concrete is needed to make the stairs? 3 ft 2 ft 8 ft 5 ft [? ] ft ³ 2 ft 8 ft 1 ft
Answers
The amount of concrete needed to make the stairs that leads to the garage is 64 cubic feet
Calculating the amount of concrete needed to make the stairs?The missing information is added as an attachment
The concrete needed to make the stairs is the volume of the stairs and this is calculated using
Volume = Base area * Height
Where
Base area = 3 * 2 + 2 * 1
Base area = 8
And
Height = 8
So, we have
Volume = 8 * 8
Evaluate
Volume = 64
Hence, the amount needed is 64 cubic feet
Read more about volume at
https://brainly.com/question/463363
#SPJ1
Which of these is a pythagorean triple?
Responses
9, 40, 41
7, 26, 89
1, 2, 3
36, 48, 62
Answers
Answer:
The first one
Step-by-step explanation:
Use the pythagoras theorem=a ^2+b^2 =c^2
Use a is 9 b is 40 because the largest value is always the hypotenuse and the hypotenuse is always c.
so you do 9 squared add 40 squared to find c squared.
Square root the answer and you get 41 so it is a pythagoras triple
at 3:25 p.m., two trains left kalamazoo, michigan. one train traveled westward at a constant rate of
Answers
When they are 111 miles apart, the current time is 4:10 p.m.
If the time taken for two trains to be apart by 111 miles by "t" time.
Then at that time, t, the train which is at 82 mph, should have traveled a distance of 82T miles.
d1 = 82t
At the same time, t, the train which is at 66 mph, should have traveled a distance of 66T miles.
d2= 66t
The total distance traveled by both trains is d1 + d2 = D
D = 82t + 66t
D = 148t
From the given data, D = 111
Hence, 148t = 111
Solving the equation, the time t
t = 111÷148
t = 0.75
Converting it into minutes,
t = 0.75*60
t = 45 mins.
The current time ( T ) = the time at which both the trains left ( t1 ) + 45 mins.
T = t1+t
T = 3:25 + 45 min.
T =4:10 pm
Therefore, the current time is 4:10 p.m
To know about Time traveled problems:
https://brainly.com/question/2854969
The complete question is-
At 3:25 p.m., two trains left Kalamazoo, Michigan. one train traveled westward at a constant rate of 82 miles per hour, while the other traveled eastward at a constant rate of 66 miles per hour. if they are now 111 miles apart, what time is it now? show your work on how you solved this situation.
given the following frequency table of values, is the mean, median, or mode likely to be the best measure of the center for the data set? valuefrequency 351 364 376 386 395 631
Answers
For the given following frequency table of values 351, 362, 373, 381, 391, The mode is likely to be the best measure of the center for the data set.
The given frequency table is as follows:
Value frequency 351, 362, 373, 381, 391.
To find the most appropriate measure of central tendency for a dataset, we need to analyze the spread of data.
The mean, median, and mode are measures of central tendency in statistics.
We can find the following measures from the given data set:
Mean: It is calculated by summing up all the values and then dividing the result by the total number of values. This measure of central tendency is appropriate when the data are symmetrical.
Median: It is the middle value of the data set when arranged in order. It is suitable for skewed data.
Mode: It is the most common value in the data set. It is appropriate when data is discrete. The data in the frequency table appear to be discrete.
Because the data are discrete, the most appropriate measure of central tendency is the mode. So, the mode is likely to be the best measure of the center for the given value frequency data set.
Learn more about the mean, median, and mode at: https://brainly.com/question/14532771
#SPJ11
What is the endpoint of a line segment with these points? Endpoint: Z(–21, 15) Midpoint: M(–13, 29) (–5, 43) (–17, 22) (–27, 21) (–29, 1)
Answers
Midpoint formula: (x1 + x2)/2, (y1 + y2)/2 = (x, y)
We can plug in the values we know:
(x1 + x2)/2 = -13
(y1 + y2)/2 = 29
x1 = -21
y1 = 15
Solving for x2 and y2:
x2 = -2x1 - 26 = -2(-21) - 26 = 16
y2 = 2y1 - 18 = 2(15) - 18 = 12
Therefore, the endpoint of the line segment with endpoint Z(–21, 15) and midpoint M(–13, 29) is E(16, 12).
Answer: A - (-5, 43)
Step-by-step explanation:
What is the value of k?
127.3°
Answers
. In which step does a mistake first occur?
(24+3 + 10)-14 + 2
Step 1: (8 + 10) -14 + 2
Step 2: 18 -14+2
Step 3: 4 +2
Step 4: 2
NEED HELP ASAP !!
TY
Answers
Answer:
The first one...............
Which of the following is a point of tangency on the circle below?
A. Point Y
B. Point Z
C. Point W
D. Point X
Answers
Based on the diagram, the point of tangency is Point Z. Therefore, the answer is B.
What is point of tangency?A point of tangency is a point at which a straight line, called a tangent line, touches a curve or a circle at only one point.
At the point of tangency, the tangent line is perpendicular to the radius of the circle that intersects the point of tangency.
The point of tangency is the point where a tangent line to the circle touches the circle at only one point.
In the given diagram, the line segment XZ appears to be a tangent to the circle.
Therefore, the point of tangency is the point where the line segment XZ touches the circle.
To know more about tangent line visit:
https://brainly.com/question/30162653
#SPJ9
the volume of a cube decreases at a rate of 6 m 3 / s . find the rate at which the side of the cube changes when the side of the cube is 4 m . answer exactly or round to 2 decimal places.
Answers
The rate at which the side of the cube changes when the side of the cube is 4 m is -1/8 m/s (or approximately -0.125 m/s).
Let's use the formula for the volume of a cube:
V = s³
where V is the volume and s is the length of one side of the cube. To find the rate of change of the side length, we need to differentiate this formula with respect to time t:
dV/dt = d/dt (s³) = 3s² ds/dt
We know that dV/dt = -6 m³/s (the negative sign indicates that the volume is decreasing), and when s = 4 m, we have:
-6 = 3(4²) ds/dt
Simplifying this equation gives us:
ds/dt = -6 / (3*4²) = -1/8 m/s
Learn more about cube here: brainly.com/question/30962206
#SPJ4
consider the differential equation given by[math equation]the goal of this problem is to solve this differential equation numerically, analytically and compare the solutions. find the exact solution (i.e. the analytical solution) use euler's method to solve the differential equation with a step size h=0,001; (this is the numerical solution)
Answers
The number of iterations increases. If there is a significant difference between the two solutions, we may need to investigate the numerical method used or check for errors in our analytical solution.
Step-by-step explanation:
The differential equation is missing in your question. However, I will give a general overview of how to solve a differential equation numerically using Euler's method and how to find an analytical solution.
Numerical Solution using Euler's Method:
Suppose we have a first-order differential equation of the form y' = f(x, y), where y' represents the derivative of y with respect to x. To solve this numerically using Euler's method, we need to start with an initial condition y(x0) = y0, and we want to find the value of y at some other point x1 = x0 + h.
The Euler's method involves approximating the derivative y' by the difference quotient (y1 - y0) / h, where y1 is the value of y at x1. Rearranging this equation, we get:
y1 = y0 + h * f(x0, y0)
Using this equation, we can iteratively compute the value of y at different points by using the previous value of y. For example, to find y2, we can use the equation:
y2 = y1 + h * f(x1, y1)
We continue this process until we reach the desired endpoint.
Analytical Solution:
An analytical solution to a differential equation is an explicit expression for y(x) that satisfies the differential equation for all values of x. To find an analytical solution, we may use techniques such as separation of variables, integrating factors, or other methods specific to the type of differential equation.
For example, if we have a differential equation of the form y' = k * y, where k is a constant, we can use separation of variables to obtain:
dy / y = k * dx
Integrating both sides, we get:
ln|y| = k * x + C
where C is an arbitrary constant of integration. Solving for y, we get:
y = Ce^(kx)
where C = ±e^C is a constant determined by the initial condition.
Comparison of Solutions:
Once we have the numerical and analytical solutions, we can compare them by plotting the graphs of y(x) for each method. If the numerical solution was computed with a small enough step size, it should converge to the analytical solution as the number of iterations increases. If there is a significant difference between the two solutions, we may need to investigate the numerical method used or check for errors in our analytical solution.
To learn more about approximating visit:
https://brainly.com/question/30945002
#SPJ11
A triangle with side lengths 7, 6, 4 is
Acute
Right
Obtuse
Answers
Right
so 7 is the hypotenuse because it is the biggest. so you have to use 6 and 4 in the formula to see if they equal 7.
(a)²+(b)²=c²
(6)²+(4)²=c²
36+16=c²
(square root) 52=c²
the square root of 52 is 7
so therefore it is a right triangle.
PLEASE HELP!
The sum of the roots of a monic quadratic is -6, and the product of its roots is 7. What is the quadratic?
Answer with a quadratic expression using the variable x such as x^2 + 10x + 20
Answers
Answer:
x^2 +6x+7
Step-by-step explanation:
for roots a and b
x^2 - (a+b)x + ab = (x-a)(x-b)
if you're good at quadratics...
Answers
Therefore, the correct answer is: [tex](x+10)^2=82[/tex]. ( right hand side of the equation).
What is equation?An equation is a mathematical statement that indicates that two expressions are equal. It typically contains variables, which are represented by letters, and may also include constants and operators. The general format of an equation is:
expression = expression
For example, the equation x + 2 = 6 means that the expression x + 2 is equal to the expression 6. The goal of solving an equation is to find the value(s) of the variable(s) that make the equation true.
To solve the quadratic equation by completing the square, Jamie needs to follow the steps:
Move the constant term to the right-hand side of the equation:
[tex]x^2 + 20x = -18[/tex]
Add and subtract the square of half the coefficient of x to the left-hand side of the equation:
[tex]x^2 + 20x + (20/2)^2 - (20/2)^2 = -18[/tex]
[tex](x+10)^2 - 100 = -18[/tex]
Simplify the right-hand side of the equation:
[tex](x+10)^2 = 82[/tex]
To know more about coefficient, visit
https://brainly.com/question/30066987
#SPJ1
Prove that the following statement is false. There exists an integer n such that 6n2 + 27 is prime. To prove the statement is false, prove the negation is true. Write the negation of the statement. For every integer n, 6n² + 27 is prime. For every integer n, 6n2 + 27 is not prime. There exists an integer n, such that 6n2 + 27 is not prime. There exists a composite number q = 6n2 + 27, such that n is an integer. There exists an integer n, such that 6n2 + 27 is prime. Now prove the negation. Suppose n is any integer. Express 6n2 + 27 as the following product: 6n2 + 2 Now is an integer because sums and products of integers are integers. Thus, 6n2 + 27 is not prime because it is a
Answers
The negation of the statement "There exists an integer n such that 6n2 + 27 is prime" is "For every integer n, 6n2 + 27 is not prime."
To prove the negation, we can use algebraic manipulation to show that 6n2 + 27 is always composite.
Suppose n is any integer. We can factor out 3 from 6n2 + 27 to get 3(2n2 + 9). Since 2n2 + 9 is always odd (2 times any integer is even, and adding 9 makes it odd), we can further factor it as (2n2 + 9) = (2n2 + 6n + 9 - 6n) = [(2n+3)(n+3)] - 6n.
Substituting this expression back into 3(2n2 + 9), we get 3[(2n+3)(n+3) - 6n]. Since (2n+3)(n+3) - 6n is an integer, 3[(2n+3)(n+3) - 6n] is composite for every integer n. Therefore, 6n2 + 27 is not prime for any integer n.
For more questions like Integer click the link below:
https://brainly.com/question/490943
#SPJ11
x^2-3x-40=0 solve for x
Answers
Answer:
Step-by-step explanation:
x^2-3x-40=0
x^2-3x=40
2x-6x=40
-4x=40
-4x/4 = 40/-4
x= -10
Answer:
x=8 or x=-5
Step-by-step explanation:
x²-3x-40=0
x²-8x+5x-40=0
x(x-8)+5(x-8)=0
(x-8)(x+5)=0
⇒x=8 or x=-5
a cable tv receiving dish is in the shape of a paraboloid of revolution. find the location of the receiver, which is placed at the focus, if the dish is 6 feet across at its opening and 2 feet deep.
Answers
the receiver is located at (0, 0, 2.25 feet) or (0, 0, 27 inches).To find the location of the receiver, we first need to determine the equation of the paraboloid.
The standard equation for a paraboloid of revolution with a vertical axis is:
z = [tex](x^2 + y^2)[/tex]/(4f)
Where:
z is the height at any point (x, y) on the paraboloid.
x and y are the horizontal coordinates of the point.
f is the focal length of the paraboloid, which is half the depth of the dish.
In this case, the dish is 6 feet across at its opening, so the diameter is 6 feet and the radius is 3 feet. Therefore, the maximum value of x and y is 3 feet. The depth of the dish is given as 2 feet.
Using these values, we can solve for the focal length:
2 = [tex](3^2 + 3^2)[/tex]/(4f)
2 = 18/(4f)
f = 18/8 = 9/4 = 2.25 feet
Now that we have the value of f, we can find the location of the receiver, which is placed at the focus of the paraboloid. The focus is located at (0, 0, f).
Therefore, the receiver is located at (0, 0, 2.25 feet) or (0, 0, 27 inches).
Learn more about equation here
https://brainly.com/question/29657992
#SPJ4
A business owner applies for a credit card to cover $14,000 in emergency expenses. The credit card charges 16.99% annual interest compounded continuously. If no payments are made for 2 years, what will the balance on the card be, rounded to the nearest penny?
Answers
Credit card charges $19665.33 will the balance on the card be, rounded to the nearest penny.
What is interest in simple words?
When you borrow money, you must pay interest, and when you lend money, you must charge interest. The most common way to represent interest is as a percentage of a loan's total amount per year. The interest rate for the loan is denoted by this proportion.
Interest is the cost of borrowing money and is typically stated as a percentage, such an annual percentage rate (APR). Lenders may charge interest to borrowers for the use of their funds, or borrowers may charge interest to lenders for the use of their funds.
amount applied for = $14,000
interest rate = 16.99%
the balance after 2 years
P₀ = $1400
r = 16.99% = 0.1699
t = 2
[tex]P_{0} = P_{0}e^{rt}[/tex]
[tex]P_{2} = 1400e^{0.1699 * 2}[/tex]
≈ $19665.33
Learn more about Interest
brainly.com/question/30393144
#SPJ1
Physics graduate student Laura Van Ertia has conducted a complete randomized design with a single factor, hoping to solve the mystery of the unified theory and complete her dissertation. The results of this experiment are summarized in the following ANOVA display:What is the sum of squares for the factor?
Answers
Remember, accurate interpretation of the results is essential for the success of Laura's dissertation.
The sum of squares for the factor in Laura Van Ertia's experiment can be found in the ANOVA display. ANOVA stands for Analysis of Variance, and it is a statistical method used to compare the means of two or more groups. The sum of squares is a measure of the variation within the data, and it helps to determine whether the differences between groups are statistically significant.
In the given question, you have not provided the actual ANOVA display, which is necessary to determine the sum of squares for the factor. The ANOVA table typically consists of columns for sources of variation (such as between groups and within groups), degrees of freedom, sum of squares, mean squares, F-ratio, and p-value. The sum of squares for the factor can be found in the 'sum of squares' column corresponding to the between-group variation row.
Once you have the ANOVA display, locate the sum of squares for the factor and use it in your analysis to understand the results of the experiment and its implications on the unified theory.
for such more questions on Analysis of Variance
https://brainly.com/question/28566238
#SPJ11
what is the value of t?
Answers
Answer:
t=36°
Step-by-step explanation:
90-54=36
opposite angles are equal so t=36°
Given f(x)=5x+7 and g(x)=2x+2, find g(g(1-3w))
Enter as the final value or expression without parentheses
Answers
As a result, the final number or expression is g(g(1-3w)) ≈ -12w + 10 (without parenthesis).
Which of these are they known as?When adding extraneous information or perhaps an afterthought to a sentence, parentheses, a pair or punctuation marks, are most frequently utilized. Two curving vertical lines can be seen in parentheses: ( ).
We must first evaluate g(1-3w) and then re-insert that result into g(x) in order to determine g(g(1-3w)).
We must first determine g(1-3w):
Substitute x with 1-3w to get g(x) ≈ 2x + 2 and g(1-3w) ≈ 2(1-3w) + 2.
g(1-3w) ≈ 2 - 6w + 2 (distribute the 2)
g(1-3w) ≈ -6w + 4 (combine similar terms) (combine like terms)
We can again again enter the result of g(1-3w) into g(x):
If you substitute g(1-3w) for x, then g(x) ≈ 2x + 2 g(g(1-3w)) ≈ 2(-6w Plus 4) + 2
g(g(1-3w)) ≈ -12w + 8 + 2 (allocate the 2) (distribute the 2)
g(g(1-3w)) ≈ -12w + 10 (combine comparable terms) (combine like terms)
To know more about parentheses visit:
https://brainly.com/question/28146414
#SPJ1
John is making apple pies and apple cobblers to sell at his stand at the Farmer's Market.
A pie uses 4 cups of apples and 3 cups of flour.
A cobbler uses 2 cups of apples and 3 cups of flour.
John has 16 cups of apples and 15 cups of flour.
When John sells the pies and cobblers at the Farmer's Market, he will make $3.00 profit per pie and $2.00 profit per cobbler.
Let x = the number of pies John makes.
Let y = the number of cobblers John makes.
Enter the four constraints into the graphing calculator.
What are the vertices of the feasible region?
Hint: input your answers from questions 3, 4, and 5 into Desmos to find the vertices.
Answers from questions 3, 4, and 5
[tex]4x+2y≤16\\3x+3y≤15\\x≥0\\y≤0[/tex]
Answers
Answer:huh,
Step-by-step explanation:I don’t understand you’re saying
I need help with dis math
Answers
3s + 7.99 = 71.83
the answer is that because u have three identical so 3s as s is shirts and u add the 7.99 as a fee and it all equals to 71.83
What is the simplest form of 8(5k+7)−10(6k−7)
Answers
The simplest form of the given expression is -20k + 126.
To find the simplest form of the expression 8(5k+7)−10(6k−7), follow these steps:
1. Distribute the numbers outside the parentheses to the terms inside the parentheses:
8 × 5k + 8 × 7 - 10 × 6k + 10 × 7
2. Perform the multiplication:
40k + 56 - 60k + 70
3. Combine like terms (terms with the same variable and exponent):
(40k - 60k) + (56 + 70)
4. Simplify the expression by performing the subtraction and addition:
-20k + 126
The simplest form of the given expression is -20k + 126.
for such more question on simplest form
https://brainly.com/question/344788
#SPJ11
PLEASE HELP AND PLEASE SHOW ALL STEPS IT WOULD BE VERY MUCH APPRECIATED!!
Answers
Answer:
I got to #1 and #3 but I didn't finish in time and I have to leave before I can finish the other ones, my apologies. The solve and steps for 1 and 3 are below. If no one has answered the other two I can probably solve the other two later tonight!
Hope this helps!
if one flag pole is y feet tall and casts a shadow x feet long, then how tall is another nearby flag pole that casts a shadow p feet long at the same time of day?
Answers
If one flag pole is y feet tall and casts a shadow x feet long, and another nearby flag pole casts a shadow p feet long at the same time of day, we can use similar triangles to determine the shadow of the second flag pole.
In this scenario, the two flag poles and the ground form two similar right triangles. The height of the first flag pole (y) corresponds to one leg of the first triangle, and the length of its shadow (x) corresponds to the other leg.
Similarly, the height of the second flag pole (h) corresponds to one leg of the second triangle, and the length of its shadow (p) corresponds to the other leg.
Therefore, the height of the second flag pole is equal to the product of the height of the first flag pole and the length of the shadow of the second flag pole, divided by the length of the shadow of the first flag pole.
For more details about shadow click here:
https://brainly.com/question/31162142#
#SPJ11
Line segment AB in the coordinate plane has endpoints with coordinates A (1,5) and B (9,17). Which of the following is true?
Answers
The correct option- The perpendicular bisector of AB has the slope -1/3.
Explain about the slope of line?The difference between the change in y-values and the change in x-values is known as the slope of a line. This figure represents the slope of a line.
A quantity called the slope of a line is used to quantify how steep a line is. This number may be zero, positive, or negative. Moreover, it may be unreasonable or rational.Any two lines with the same slope are said to be parallel. When a line is rotated 90 degrees, it becomes perpendicular and becomes parallel. Four 90 degree angles result from the intersection of two perpendicular lines.Formula for slope m = (y2 - y1)/(x2 - x1)
Line segment AB coordinates :
A (1,5) and B (9,17).
Slope m1 = (17 - 5)/(9 - 5)
m1 = 12/4
m1 = 3
The line perpendicular to AB.
Let the slope of m2.
The relation between the slopes of perpendicular lines:
m1 x m2 = -1
3 x m2 = -1
m2 = -1/3.
Thus, the slope of the line perpendicular to the given line AB is found as: -1/3.
Know more about the slope of line
https://brainly.com/question/16949303
#SPJ1
Complete question:
AB in the coordinate plane has endpoints with coordinates A (1,5) and B (9,17). Which of the following is true?
The perpendicular bisector of AB has slope 3/2.
The perpendicular bisector of AB has slope -2/3.
The perpendicular bisector of AB has slope -2/3.
The perpendicular bisector of AB has slope -1/3.
a high school baseball player has a 0.253 batting average. in one game, he gets 8 at bats. what is the probability he will get at least 6 hits in the game?
Answers
The probability of a high school baseball player getting at least 6 hits in one game, given a 0.253 batting average, when he gets 8 at-bats, is 0.0197 or approximately 2%.
Given, the high school baseball player's batting average is 0.253, which means in 100 times he hits the ball, he will make 25.3 hits on average. We need to find the probability of getting at least 6 hits in a game when he gets 8 at-bats.
We will calculate the probability using the Binomial Probability formula. Here, the number of trials is 8, and the probability of success is 0.253. We need to find the probability of getting at least 6 hits.
P(X≥6) = 1 - P(X<6)
P(X<6) = ∑P(X=i), i=0 to 5
We can use the Binomial Probability Table to find these probabilities or use the Binomial Probability formula.
P(X<6) = P(X=0) + P(X=1) + P(X=2) + P(X=3) + P(X=4) + P(X=5)
= C(8,0) (0.253)^0 (1 - 0.253)^8 + C(8,1) (0.253)^1 (1 - 0.253)^7 + C(8,2) (0.253)^2 (1 - 0.253)^6 + C(8,3) (0.253)^3 (1 - 0.253)^5 + C(8,4) (0.253)^4 (1 - 0.253)^4 + C(8,5) (0.253)^5 (1 - 0.253)^3
≈ 0.9799
Therefore, P(X≥6) = 1 - 0.9799
= 0.0201 or approximately 2%.
Hence, approximately 0.0197 or 1.97% is the probability of a high school baseball player, who has a batting average of 0.253, obtaining at least 6 hits when given 8 at-bats during a single game.
To know more about probability refer here:
https://brainly.com/question/1596693#
#SPJ11