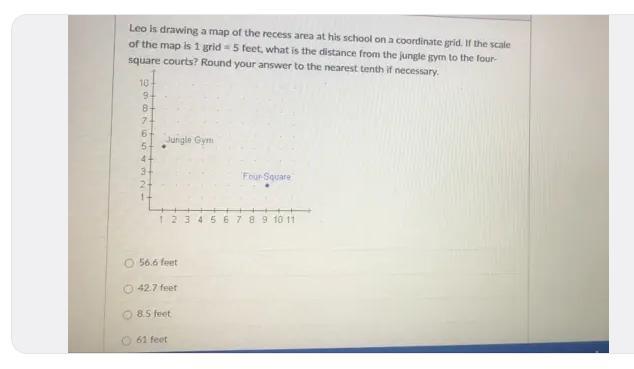
Leo is drawing a map of the recess area at his school on a coordinate grid. If the scale of the map is 1 grid = 5 feet, what is the distance from the jungle gym to the four-square courts? Round your answer to the nearest tenth if necessary.

Try going to the store and they should be surprisingly cheap.

Answer: here it is.

Step-by-step explanation:

Algebraic expressions are useful for solving different and complex equations in mathematics, as well as for modelling real-life situations such as revenue, cost, inference, etc

The algebraic expression is: [tex]6x - 9[/tex].

To represent the sentence as an algebraic expression, we can follow these steps: Identify the variable. In this case, “a number” is x. Identify the operation. In this case, “less than” means subtraction and “times” means multiplication.

An algebraic expression is an expression that contains variables, constants and mathematical operations. Algebraic expressions are useful because they can help us solve different and complex equations.

For example, if you want to calculate the area of a rectangle with length x and width y, you can use the algebraic expression xy to represent the area.

Write the expression using the order of operations. In this case, we need to multiply six by x first, then subtract nine from the result.

Therefore, The algebraic expression is: [tex]6x - 9[/tex]

Learn more about expression here:

https://brainly.com/question/953809

#SPJ1

The quadratic equation in the given graph can be written in the vertex-form as:

y = -2(x - 1)² + 4

We can see the graph of a quadratic equation. Remember that a quadratic equation with a vertex (h, k) and a leading coefficient a can be written as:

y = a*(x - h)² + k

in the graph we can see that the vertex is (1, 4), replacing that we will get:

y = a*(x - 1)² + 4

In the graph we also can see that the curve passes through the point (0, 2), replacing thesevalues in the equation we will get:

2 = a*(0 - 1)² + 4

2 = a + 4

-2 = a

Then the quadratic is:

y = -2(x - 1)² + 4

Learn more about quadratic equations at:

https://brainly.com/question/1214333

#SPJ1

Answer:

To calculate the payback period (PBP) for this project, we need to determine how long it will take for the initial cash outlay of $40,000 to be recovered from the after-tax cash flows.

Year 1 cash flow = $10,000

Year 2 cash flow = $12,000

Year 3 cash flow = $15,000

Year 4 cash flow = $10,000

Year 5 cash flow = $7,000

Total cash inflows for year 1 and year 2 = $10,000 + $12,000 = $22,000

Total cash inflows for year 3 = $15,000

Total cash inflows for year 4 = $10,000

Total cash inflows for year 5 = $7,000

Cumulative cash inflows for year 1 and year 2 = $22,000

Cumulative cash inflows for year 3 = $37,000

Cumulative cash inflows for year 4 = $47,000

Cumulative cash inflows for year 5 = $54,000

It can be seen that the cumulative cash inflows reach the initial cash outlay of $40,000 after year 2, and therefore the payback period for this project is 2 years. Since the payback period is less than the maximum PBP of 3.5 years set by management, this project can be considered acceptable.

So, Hodgman Honest should recommend that Basket Wonders should accept this project as it has a payback period of only 2 years, which is less than the maximum PBP of 3.5 years set by management.

Answer:

First, we need to find the radius of the base of the cone. We can see from the grid that the diameter is 8 units, so the radius is 4 units (or 4 feet).

Next, we can use the formula for the volume of a cone to find the height:

V = (1/3)πr^2h

Substituting the given volume and radius, and using 3.14 for π, we get:

200.96 = (1/3) x 3.14 x 4^2 x h

Simplifying and solving for h, we get:

h = 200.96 / (1/3 x 3.14 x 4^2)

h = 200.96 / 53.02

h ≈ 3.79 feet (rounded to two decimal places)

To construct the cone vertically on the grid with respect to the center of the base, we can draw a circle with radius 4 units (or 4 feet) centered at the point (4,4) on the grid. Then, we can draw a line from the center of the circle (point (4,4)) up to a point above the circle that is 3.79 units (or 3.79 feet) away from the center. This line represents the height of the cone. Finally, we can connect the endpoint of the line to the points where the circle intersects the grid to complete the cone.

Answer: 260 ft^2

Step-by-step explanation:

Find the area of the triangle: 0.5*height*base = 0.5*10*20 = 100 ft^2

Find the area of the rectangle: 20*8 = 160 ft^2

Add them together: 160+100 = 260 ft^2

Answer:

y=2x+10

Explanation: They start with paying $10 and have to pay and extra $2 for each time at the concession stand.

Answer:

The given expression is:

3x + 2 / (x + 1)(x² + x + 2)

To simplify this expression, we need to factor the denominator first:

x² + x + 2 = (x + 2)(x + 1)

So the expression becomes:

3x + 2 / (x + 1)(x + 2)(x + 1)

Next, we can use partial fraction decomposition to express the expression in terms of simpler fractions. Let's assume:

3x + 2 / (x + 1)(x + 2)(x + 1) = A/(x + 1) + B/(x + 2) + C/(x + 1)²

Multiplying both sides by the common denominator, we get:

3x + 2 = A(x + 2)(x + 1) + B(x + 1)² + C(x + 2)(x + 1)

Expanding the right side, we get:

3x + 2 = Ax² + 3Ax + 2A + Bx² + 2Bx + B + Cx² + 3Cx + 2C

Combining like terms, we get:

3x + 2 = (A + B + C)x² + (3A + 2B + 3C)x + (2A + B + 2C)

Since this equation holds for all values of x, the coefficients of each power of x must be equal on both sides. We can equate the coefficients of x², x, and the constant term to get a system of three equations for A, B, and C:

A + B + C = 0

3A + 2B + 3C = 3

2A + B + 2C = 2

Solving this system, we get:

A = 2/3

B = -1/3

C = -1/3

Substituting these values back into the partial fraction decomposition equation, we get:

3x + 2 / (x + 1)(x² + x + 2) = 2/3/(x + 1) - 1/3/(x + 2) - 1/3/(x + 1)²

Therefore, the simplified expression is:

3x + 2 / (x + 1)(x² + x + 2) = 2/3/(x + 1) - 1/3/(x + 2) - 1/3/(x + 1)²

Answer: yes correct i love math

Step-by-step explanation:

Answer:

"Undefined slope"

Step-by-step explanation:

The line is vertical on the graph.

Every point on the line has the same x-coordinate.

If the line crosses the x-axis where x=-7, then the

x-coordinate of every point on the line is -7, and the

equation of the line is

                                     x = -7 .

The expressions can be written as  :a. log5.625 ≈ 0.75.

                                                             b. log6.4 + log6.12 ≈ 1.67.

                                                             c. log3.9^{4} ≈ 2.47.

What is logarithm function?

A logarithm function is a mathematical function that determines the power to which a fixed number, called the base, must be raised to produce a given value and The logarithm function is the inverse of the exponential function. The most commonly used base for logarithmic functions is 10 (log base 10), but other bases such as 2 (log base 2) and the natural logarithm base e (ln) are also used.

a. Since there is no base specified, we assume the base to be 10 by default. Therefore, we can write:

log5.625 = log(5625/1000)

Using the property log(a/b) = log(a) - log(b), we can simplify this expression to:

log5.625 = log(5625) - log(1000)

Using the change of base formula, we can convert the logs to a common base, such as 2 or e:

log5.625 = log(5625)/log(10) - log(1000)/log(10)

Evaluating the logs using a calculator or by simplifying, we get:

log5.625 ≈ 0.75

Therefore, log5.625 ≈ 0.75.

b. Using the property log(a) + log(b) = log(ab), we can simplify the expression:

log6.4 + log6.12 = log(6.4 × 6.12)

Using the change of base formula, we can convert this to a common base:

log6.4 + log6.12 = log(6.4 × 6.12)/log(10)

Evaluating the log using a calculator or by multiplying 6.4 and 6.12 and simplifying, we get:

log6.4 + log6.12 ≈ 1.67

Therefore, log6.4 + log6.12 ≈ 1.67.

c. Using the property log(a^{n}) = n log(a), we can simplify the expression:

log3.9^{4} = 4 log3.9

Using the change of base formula, we can convert this to a common base:

log3.9^{4} = 4 log(3.9)/log(10)

Evaluating the log using a calculator or by simplifying, we get:

log3.9^{4} ≈ 2.47

Therefore, log3.9^{4} ≈ 2.47.

To learn more about logarithm function, visit the link:

https://brainly.com/question/13473114

#SPJ1

Answer:

147

Step-by-step explanation:

A= h^b b=21*14= 147

The calculated value of the force of the resistance is 15.62 N

We can use Newton's Second Law of Motion to solve this problem. The formula is:

F = m*a

where F is the net force, m is the mass of the object, and a is the acceleration.

In this case, the brick is falling through water, so there are two forces acting on it:

The net force is the difference between these two forces:

F_net = F_gravity - F_resistance

The weight of the object is:

F_gravity = m*g

So, we have

F_gravity = 2 kg * 9.81 m/s^2 = 19.62 N

Now we can use the formula for net force to find the force of water resistance:

F_net = F_gravity - F_resistance

F_resistance = F_gravity - F_net

F_resistance = 19.62 N - m*a

This gives

F_resistance = 19.62 N - 2 kg * 2 m/s^2 = 15.62 N

Therefore, the force of water resistance is 15.62 N.

Read more about force at

https://brainly.com/question/13370981

#SPJ1

Answer:

3. 216 cm^3

4a. A = 5 ft, B = 4 ft.

4b. 88 ft^3

Step-by-step explanation:

3. Separate into two rectangular prisms:

Volume of first one: 4cm*2cm*3cm = 24cm^3

Volume of second one: 4cm*12cm*4cm = 192cm^3

Add them together: 24 + 192 = 216cm^3

4a.

Length A = 8-3 = 5ft.

Width B = 8-4 = 4ft.

4b. Separate into two rectangular prisms:

Volume of first one: 2ft*3ft*4ft = 24ft^3

Volume of second one: 8ft*4ft*2ft = 64ft^3

Add them together: 24 + 64 = 88ft^3

Answer: no they wouldn't be similar

Step-by-step explanation: if x=60 if triangle 1 then the third angle would be (180-(58+60)) =180-118=62
if we decide to calculate the third angle in triangle 2 we will have 180-(50+58) = 180-108=72

therefore not all angles in 1 are similar to angles in 2 so the triangles aren't similar

Step-by-step explanation:

2  2/3 =  8/3

8/3 * 1/4  = 8/12 =   2/3 pound in each portion

The resulting number is 12/5

Arithmetic operations is a branch of mathematics, that involves the study of numbers, operation of numbers that are useful in all the other branches of mathematics. It basically comprises operations such as Addition, Subtraction, Multiplication and Division.

Given that we need to, increase the number 15/16 by 3/5 of it, then increase the resulting number by 3/5 of it

So, performing the operations,

15/16+15/16×3/5

= 15/16(1+3/5)

= 15/16(8/5)

= 120/80

= 3/2

Now,

3/2+3/2×3/5

= 3/2(1+3/5)

= 3/2(8/5)

= 24/10

= 12/5

Hence, the resulting number is 12/5

Learn more about arithmetical operations, click;

https://brainly.com/question/30553381

#SPJ2

The probability of rolling an even number on a single die is 1/2, or 50%. This can be calculated by considering the possible outcomes of rolling the die.

There are six possible outcomes, and three of these are even numbers (2, 4, and 6). Therefore, there is a 3/6, or 1/2, chance of rolling an even number. In terms of probability, this can be expressed as a fraction, percentage, or decimal. As a fraction, the probability of rolling an even number on a single die is 3/6, or 1/2. As a percentage, the probability of rolling an even number on a single die is 50%. As a decimal, the probability of rolling an even number on a single die is 0.5. No matter how it is expressed, the probability of rolling an even number on a single die is 1/2, or 50%. This can be easily remembered by considering that there are six possible outcomes, and three of them are even numbers.

Learn more about probability here:

https://brainly.com/question/15124899

#SPJ1

Step-by-step explanation:

To find the percentage that $4250 represents of $6500, we can use the following formula:

percentage = (part / whole) x 100%

where "part" is $4250 and "whole" is $6500.

Substituting these values into the formula, we get:

percentage = (4250 / 6500) x 100%

percentage = 0.6538 x 100%

percentage = 65.38%

Therefore, $4250 represents 65.38% of $6500.

Answer: It is approximately 65%

Step-by-step explanation: Divide $4,250 by $6,500 and your answer without rounding is 65.3846%

A square is not created when a plane slices through a cone.

What is square?

A square is a geometrical shape that has four equal sides and four equal angles of 90 degrees.

What is cone?

A cone is a three-dimensional geometric shape that tapers smoothly from a flat base to a pointed top or apex. It looks like a funnel or an ice cream cone.

When a plane intersects or slices through a cone, it creates a variety of different shapes depending on the angle of the plane and the position of the cone.

If the plane intersects the cone at an angle perpendicular to its base, it will create a circle. If the plane intersects the cone at an angle that is not perpendicular to its base, it will create an ellipse.

If the plane intersects the cone at an angle that is parallel to one of its generators (the lines that can be drawn from the vertex of the cone to any point on its base), it will create a parabola. If the plane intersects the cone at an angle that is not parallel to one of its generators, it will create a hyperbola.

Therefore, a square is not created when a plane slices through a cone.

To learn more about cone visit:

https://brainly.com/question/1082469

#SPJ9

Therefore , the solution of the given problem of percentage comes out to be the firm expects that each warranty it sells will be worth $1.41.

In statistics, "a%" is used to refer to a figure or number that is expressed as a percentage of 100. Additionally rare are the forms that "pct," "pct," or "pc". It is typically represented by the symbol "%," though. Additionally, there are not any indicators and the proportion of each item to the overall amount is flat. Since percentages typically add up to 100, they are essentially integers. Either the expression "fraction" or the symbol for percentage (%) .

Here,

The price to substitute each item is $200. The anticipated price for each component is thus:

Expected cost per product equals Replacement cost x Failure Probability

=> Cost per product anticipated = 0.008 x $200

=>  Expected price per item is $1.60.

So, the following is the anticipated value of each warranty sold:

Expected worth of the warranty = Failure rate x (Replacement cost - Cost of warranty)

=>   Expected guarantee value = 0.008 * ($200 - $22 - $1.60).

=>  Expected guarantee value = 0.008 * $176.40

=>  Expected warranty worth is $1.41

As a result, the firm expects that each warranty it sells will be worth $1.41.

To know more about percentage visit:

https://brainly.com/question/28269290

#SPJ1

It will take around 3.72 months to pay off the credit card debt.

The formula for APR is:

A = P * [tex](1 + r/n)^{nt}[/tex]

In which,

A = amount after compounding.

P = balance amount

r = rate of interest.

n = number of time compounded.

Initial balance: $30,000.

Payments per month = $200.

Expenses = $100

Balance amount = 30,000 - 12 *(200 - 100)

Balance amount = $28800

So, time taken for paying off credit card debt.

30,000 = 28800  [tex](1 + 0.24/1)^{1*t}[/tex]

[tex](1.24)^{t}[/tex] = 30,000 / 28800

[tex](1.24)^{t}[/tex] = 1.04

Solve by using logarithmic function.

t = ln (1.04) / 1.24

t = 0.31  year

t = 3.72 months

Thus, it will take around 3.72 months to pay off the credit card debt.

Know more about the annual percentage rate APR

https://brainly.com/question/24715857

#SPJ1

This is a contradiction, so our original assumption that g(x) = f(x) must be false. Therefore, the solution is not true algebraically.

What are functions ?

In mathematics, a function is a rule that maps each element in a set (the domain) to a unique element in another set (the range). It is a relation between a set of inputs and a set of possible outputs with the property that each input is related to exactly one output. Functions are commonly represented using function notation, where the symbol "f" is used to represent the function, and the input value is placed inside parentheses. For example, if the function takes the input "x" and returns the output "y"

According to the question:
To prove algebraically that g(x) = f(x), we need to show that the expressions for g(x) and f(x) are equivalent for all values of x. That is, we need to show that:

2x²+3x-1 = x²-3

We can start by simplifying both sides of the equation:

2x²+3x-1 - (x²-3) = 0

Simplifying the left side, we get:

2x²+3x-1 - x²+3 = x²+3x+2

Now we can simplify the right side:

x²+3x+2 = (x+1)(x+2)

Substituting this expression back into the equation, we get:

2x²+3x-1 - x²+3 = (x+1)(x+2)

Simplifying the left side again, we get:

x²+3x-4 = (x+1)(x-4)

Now we have:

(x+1)(x-4) = (x+1)(x+2)

We can cancel out the factor of (x+1) from both sides, since it is not equal to zero for any value of x:

x-4 = x+2

Subtracting x from both sides, we get:

-4 = 2

This is a contradiction, so our original assumption that g(x) = f(x) must be false. Therefore, the solution is not true algebraically.

To know more about functions visit:
https://brainly.com/question/29120892
#SPJ1

The  X, Y, and Z values ​​are 84, 90, and 90, respectively. To answer this question, we need to understand the meaning of the words "median", "mean" and "range".

Median is the middle number of a set of numbers - it is the number in the middle when the numbers are ordered from smallest to largest.

Since the median is 90, this means that Y (the mean number) is 90. Since the average is 92, this means that the sum of the three numbers is 276 (92 x 3). The interval is 6, which means that the difference between the largest number and the smallest number is 6.

To solve for X and Z, we can use the equation X Y Z = 276. We know that Y is 90, so we can plug 90 into Y:

X 90 Z = 276

Then we can  subtract 90 from both sides to find the value of X and Z:

X Z = 186

Since the range of the three numbers is 6, this means that X and Z must be 6 plus. The only two numbers that differ by six and add up to 186 are 84 and 90.

Therefore the  X, Y, and Z values ​​are 84, 90, and 90, respectively.

For more questions related to interval

https://brainly.com/question/28485020

#SPJ1

Answer:

The product of two numbers is 21.

Step-by-step explanation:

If the first number is -3, which equation represents this situation and what is the second number? A. The equation that represents this situation is x − 3 = 21.

The probability that John's drive to work will take between 36 and 40 minutes is 0.3413.

Probability is the measure of how likely an event is to occur. It is expressed as a number between 0 and 1, where 0 indicates that the event is impossible and 1 indicates that the event is certain to occur. Probability is used in many areas of life, such as gambling, finance, and science. It is also used to make decisions in everyday life, such as estimating the likelihood of rain or the chance of winning a bet.

Using the normal distribution, the probability of John's drive taking between 36 and 40 minutes can be calculated using the standard normal distribution table. The formula for calculating the probability is: P(x<X<y) = P(y) - P(x).

For the given problem, the lower boundary is 36 minutes and the upper boundary is 40 minutes. Using the standard normal distribution table, the probability of John's drive taking between 36 and 40 minutes can be calculated by subtracting the probability of 36 minutes from the probability of 40 minutes. This gives us a probability of 0.3413.

Therefore, the probability that John's drive to work will take between 36 and 40 minutes is 0.3413.

To know more about probability click-
https://brainly.com/question/24756209
#SPJ1

The probability that John's drive to work will take between 36 and 40 minutes is 0.3829.

Probability is the measure of how likely an event is to occur. It is expressed as a number between 0 and 1, where 0 indicates that the event is impossible and 1 indicates that the event is certain to occur. Probability is used in many areas of life, such as gambling, finance, and science. It is also used to make decisions in everyday life, such as estimating the likelihood of rain or the chance of winning a bet.

The probability that John's drive to work will take between 36 and 40 minutes can be calculated using a normal distribution table. The mean of the distribution is µ = 38 minutes, and the standard deviation is σ = 5 minutes.

To calculate the probability, we need to convert the given range (36 minutes to 40 minutes) into standard normal scores. This is done by subtracting the mean (µ = 38 minutes) from the lower bound (36 minutes) and then dividing by the standard deviation (σ = 5 minutes). The result is a standard normal score of -0.4. The same calculation is carried out for the upper bound (40 minutes) and the result is a standard normal score of 0.4.

Using a normal distribution table, we can then determine the probability that John's drive to work will take between 36 and 40 minutes. This probability is equal to the area under the normal curve between the two standard normal scores of -0.4 and 0.4. The result is a probability of 0.3829.

Therefore, the probability that John's drive to work will take between 36 and 40 minutes is 0.3829.

To know more about probability click-
brainly.com/question/24756209
#SPJ1

The interest that is paid on the loan in 6 years will be $4,200.

The amount of interest that is saved is $2,100.

The simple interest is a linear function of the number of years of the loan, value of the loan and the duration of the loan. The higher either of these values are, the higher the simple interest.

Simple interest = loan x time x interest rate

Simple interest if the loan is paid off after 6 years: $12,500 x 6 x 0.056 = $4,200

Simple interest if the loan is paid off after 3 years: $12,500 x 3 x 0.056 = $2100

Interest saved = $4200 - $2100 = 2100

To learn more about simple interest, please check: https://brainly.com/question/27328409

#SPJ1

Answer:

31000 - y = x

Step-by-step explanation:

Solve for x

[tex]12000\times5=9500+9500+10000+x+y[/tex]

Add and multiply the integers

[tex]60000=29000+x+y[/tex]

Subtract 29000 on both sides

[tex]31000=x+y[/tex]

Subtract y on both sides

[tex]31000-y=x[/tex]