Answers
Answer:
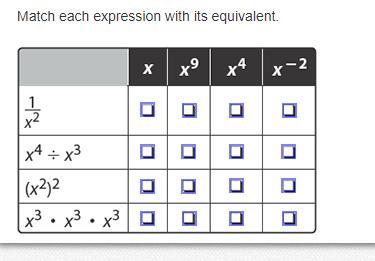
1/x^2 = x^-2
x^4/x^3 = x
(x^2)^2 = x^4
x^3 * x^3 * x^3 = x^9
Step-by-step explanation:
Related Questions
profitability empirical rule with this dataset? why or why not. no, the measures the proportion of a movies budget recovered. a profitability less than 1 the movie did not make enough money to cover the budget, while a profitability greater than means means it made a profit. a boxplot of the profitability ratings of 136 movies that came out in 2011 is shown below. (the largest outlier is the movie 1 insidi high gross revenue.)
Answers
The empirical rule does not apply to this dataset because the empirical rule is used to describe data that is normally distributed.
The empirical rule is a statistical rule that states that for a normal distribution.
Approximately 68% of the data will fall within one standard deviation of the mean, 95% of the data will fall within two standard deviations of the mean, and 99.7% of the data will fall within three standard deviations of the mean.
The dataset is normally distributedThe dataset is normally distributed, determine if the empirical rule appliesThe empirical rule does not apply, identify an alternative method to describe the datasetThe empirical rule does not apply to this dataset because the empirical rule is used to describe data that is normally distributed.
This dataset does not appear to be normally distributed, as evidenced by the large outlier (1 Insidi High Gross Revenue).
For similar question on empirical rule:
https://brainly.com/question/31627334
#SPJ11
the list shows the weight in pounds of 6 puppies at birth. 3, 1.6, 2.8, 2.5, 1.7, 2.8 what is the mean absolute deviation of these numbers?
Answers
Step 1: Find the mean (average) of the numbers.
Mean = (3 + 1.6 + 2.8 + 2.5 + 1.7 + 2.8) / 6 = 2.3667 (rounded to 4 decimal places)
Step 2: Find the absolute deviation of each number by subtracting the mean from each number and taking the absolute value.
|3 - 2.3667| = 0.6333
|1.6 - 2.3667| = 0.7667
|2.8 - 2.3667| = 0.4333
|2.5 - 2.3667| = 0.1333
|1.7 - 2.3667| = 0.6667
|2.8 - 2.3667| = 0.4333
Step 3: Find the mean of the absolute deviations.
MAD = (0.6333 + 0.7667 + 0.4333 + 0.1333 + 0.6667 + 0.4333) / 6
MAD = 0.5 (rounded to 1 decimal place)
Therefore, the mean absolute deviation of the given set of numbers is 0.5.
answer these questions
Answers
Answer:
a) model a: 50/hr
model b: 40/hr
b) model a
Step-by-step explanation:
b) since the money raised started at 0, the rate of change can be found by calculating 400/8
Can someone help me asap? It’s due tomorrow. I will give brainiest if it’s correct
Answers
Answer:
96
Step-by-step explanation:
1. In Design 2, what is the radius of the larger
grassy area?
Answers
Answer: 5 m
Step-by-step explanation:
A radius is half of the diameter which is the black line. Hope this helps!
Answer:
The radius of the larger grass area is 5m
Step-by-step explanation:
d=2r
r=d/2
r=10/2
r=5m
At midnight, the temperature in a city was 5 degrees celsius. The temperature was dropping at a steady rate of 2 degress celsius per hour. Write an inequalty that represents t, the number of hours past midnight, when the temperature was coler than -4 degrees celsius
Answers
( 5 - 2t ) < - 4 is an inequalty that represents t, the number of hours past midnight, when the temperature was coler than -4 degrees celsius.
What is linear equation?
An algebraic equation with simply a constant and a first- order( direct) element, similar as y = mx b, where m is the pitch and b is the y- intercept, is known as a linear equation.
The below is sometimes appertained to as a" direct equation of two variables," where y and x are the variables. Equations whose variables have a power of one are called direct equations. One illustration with only one variable is where layoff b = 0, where a and b are real values and x is the variable.
The midnight temperature is 5 °C and the temperature is decreasing at the rate of 2°C per hour.
If t is the hours past midnight then after t hours the temperature will be ( 5 - 2t ).
Now, if this temperature is colder than - 4° C, then the inequality can be written as ( 5 - 2t ) < - 4.
Learn more about Linear equation
brainly.com/question/11897796
#SPJ1
The inequality that represents t, the number of hours past midnight, when the temperature was cooler than -4 degrees celsius( 5 - 2t ) < - 4
What is inequality?
The term "inequality" is used in mathematics to describe a relationship between two expressions or values that is not equal to one another. Inequality results from a lack of balance. When two quantities are equal, we use the symbol '=', and when they are not equal, we use the symbol. If two values are not equal, the first value can be greater than (>) or less than (), or greater than equal to () or less than equal to ().
The midnight temperature is 5 °C and the temperature is decreasing at the rate of 2°C per hour.
If t is the hours past midnight then after t hours the temperature will be
=> ( 5 - 2t ).
Now, if this temperature is colder than - 4° C, then the inequality can be written as ( 5 - 2t ) < - 4.
To learn more about inequality refer the below link
https://brainly.com/question/25275758
#SPJ1
I NEED HELP, LIKE NOW!\
What is -27 radical 72
Answers
Step-by-step explanation:
-27 [tex]\sqrt{72}[/tex] = -27 [tex]\sqrt{36*2}[/tex] = -27 (6) [tex]\sqrt{2}[/tex] = - 162 [tex]\sqrt{2}[/tex] = - 229.1
if a garden box is 4x by 3x and the area of the box in square feet is equal to four times the perimeter in feet what is the value for x that satisfies these requirements
Answers
The answer to this question is x = 6
A company makes 110 bags. 32 of the bags have buttons but no zips. 28 of the bags have zips but no buttons. 24 of the bags have neither zips nor buttons. How many bags have zips on them?
Answers
The number of bags that have zips on them is 28.
To solve this problem, we can use the principle of inclusion-exclusion.
First, we know that the total number of bags is 110.
Next, we know that 24 of the bags have neither zips nor buttons. Therefore, the number of bags that have either zips or buttons is 110 - 24 = 86.
We also know that 32 of the bags have buttons but no zips, and 28 of the bags have zips but no buttons.
To find the number of bags that have both zips and buttons, we can subtract the number of bags that have only buttons from the total number of bags with zips, or vice versa:
Number of bags with both zips and buttons = (Number of bags with zips) + (Number of bags with buttons) - (Number of bags with either zips or buttons)
Number of bags with both zips and buttons = 28 + 32 - 86 = -26
This result is clearly nonsensical, so we can conclude that there are no bags with both zips and buttons.
Therefore, the number of bags that have zips on them is simply the number of bags with zips but no buttons, which is 28.
Learn more about principle of inclusion-exclusion here
brainly.com/question/27975057
#SPJ4
julian rolled a normal 6-sided die 12 times. his rolls were as follows: 2, 4, 3, 3, 5, 1, 2, 6, 3, 1, 3, 5, 4. what is the probability that he will roll a 3 on the next roll?
Answers
The probability that Julian will roll a 3 on the next roll is approximately 16.67%. The probability of rolling a 3 on a normal 6-sided die is independent of the previous rolls. This means that regardless of the outcomes of Julian's previous rolls, the probability remains the same.
Explanation
On a 6-sided die, there is 1 favorable outcome for rolling a 3 (the number 3 itself) out of 6 possible outcomes (1, 2, 3, 4, 5, and 6).
To find the probability, you can use the formula:
Probability = (Number of favorable outcomes) / (Total number of outcomes)
In this case:
Probability of rolling a 3 = 1 (favorable outcome) / 6 (total outcomes)
Probability of rolling a 3 = 1/6 ≈ 0.1667 or 16.67%
So, the probability that Julian will roll a 3 on the next roll is approximately 16.67%.
To learn more about probability : brainly.com/question/27292589
#SPJ11
When you went to know the mass of a bowling ball what unit do you choose
Answers
Standard unit chose to measure the mass of a bowling ball is equal to kilogram .
The unit typically used to measure the mass of a bowling ball is the pound (lb) or the kilogram (kg).
It depends on the country as different countries have different standard unit for measuring mass.
In the United States, the weight of a bowling ball is often measured in pounds.
While in many other countries, the weight is measured in kilograms.
When measuring the mass of a bowling ball,
It is important to use a calibrated scale that is designed to handle the weight of the ball.
Some scales are specifically designed for weighing bowling balls.
And they may have a higher weight capacity than a typical bathroom scale.
It is also important to ensure that the scale is on a flat, stable surface to ensure an accurate measurement.
learn more about mass here
brainly.com/question/9497577
#SPJ4
a customer spends 21.50 on cupcakes and muffins. the numbet of muffins purchased is 1 few than number of cupcakes. each cupcake costs $2, and each muffin cost $1.25 create a system of equations
Answers
Answer: Let's use the following variables to represent the unknown quantities in the problem:
x: the number of cupcakes purchased
y: the number of muffins purchased
From the problem statement, we can write two equations:
The total amount spent on cupcakes and muffins is $21.50:
2x + 1.25y = 21.50
The number of muffins purchased is one fewer than the number of cupcakes:
y = x - 1
These two equations form a system of equations that can be solved simultaneously to find the values of x and y.
Substituting equation 2 into equation 1, we get:
2x + 1.25(x - 1) = 21.50
Simplifying and solving for x:
2x + 1.25x - 1.25 = 21.50
3.25x = 22.75
x = 7
Now that we know x, we can use equation 2 to find y:
y = x - 1 = 7 - 1 = 6
Therefore, the customer purchased 7 cupcakes and 6 muffins, spending a total of $21.50.
Step-by-step explanation:
Aidan wants to find the mass of a
bowling ball.Which unit should he use
Answers
Answer:
Aiden should use the Standard unit of Mass
Kilogram.
Step-by-step explanation:
He can use other unit also like gram, pound, ounce, tone etc
pamela registered her new phone number on the do not call registry. how long will her number remain on the list?
Answers
If Pamela has registered for the first time, it will remain on the Do Not Call list permanently. If she has re-registered, it will remain on the list for an additional five years from the date of re-registration.
How long do phone numbers remain on the Do Not Call Registry?The length of time that Pamela's phone number will remain on the National Do Not Call Registry depends on whether she registered her number on the Do Not Call Registry for the first time or if she has re-registered her number after it has already been on the list for a while.
If Pamela registered her phone number for the first time, it will be added to the Do Not Call Registry within 31 days of her registration date. Her phone number will remain on the list permanently, unless she requests to remove it or the number is disconnected.
If Pamela has re-registered her phone number after it has already been on the list for a while, her number's registration will be extended for another five years from the date she re-registered it.
Therefore, if Pamela registered her phone number for the first time, it will remain on the list permanently. If she has re-registered her number, it will remain on the list for an additional five years from the date of re-registration.
Learn more about do not call registry
brainly.com/question/30780624
#SPJ11
Can someone help me on these last 3 question it’s 3,5 and 6 I js need help on these
Answers
The required area of the given triangle is 63 ft² respectively.
What is a triangle?A triangle is a 3-sided polygon that is occasionally (though not frequently) referred to as the trigon.
There are three sides and three angles in every triangle, some of which may be the same.
A unique triangle and plane (i.e., a two-dimensional Euclidean space) are determined by any three non-collinear points in Euclidean geometry.
In other words, every triangle is contained in a plane, and there is only one plane that contains that triangle.
Area of a triangle:
1/2 * b * h
Now, insert values as follows:
1/2 * b * h
1/2 * 14 * 9
7 * 9
63 ft²
Therefore, the required area of the given triangle is 63 ft² respectively.
Know more about triangles here:
https://brainly.com/question/17335144
#SPJ1
the dimensions of noah’s ark were reported as 3.0 × 102 cubits by 5.0 × 101 cubits. express this size in units of feet (1 cubit = 1.5 ft)
Answers
The dimensions of Noah's Ark in feet are 450 feet by 75 feet if the dimensions of Noah's Ark is 3.0 × 102 cubits by 5.0 × 101 cubits.
Noah's Ark is said to have dimensions of 3.0 × 10^2 cubits by 5.0 × 10^1 cubits. To convert these measurements to feet, we can use the conversion factor of 1 cubit = 1.5 feet.
First, we need to convert the length of the ark from cubits to feet. To do this, we multiply the length of the ark in cubits (3.0 × 10^2) by the conversion factor of 1.5 feet/cubit. This gives us a length of
3.0 × 10^2 cubits x 1.5 feet/cubit = 450 feet
Similarly, we can convert the width of the ark from cubits to feet by multiplying the width in cubits (5.0 × 10^1) by the conversion factor of 1.5 feet/cubit. This gives us a width of:
5.0 × 10^1 cubits x 1.5 feet/cubit = 75 feet
To know more about Ark here
https://brainly.com/question/28350760
#SPJ4
Please help me with these 4 questions
Answers
The total surface area of each figure are:
1) 2,557.3 yd²
2) 601.02 m₂
3) 3782.5 mm²
4)750 in²
How to find the total surface area?1) The total surface area of a cylinder is:
2πrh + 2πr².
where:
r is radius
h is height
Thus:
TSA = 2π(11 * 26) + 2π(11)²
TSA = 2π(286) + 2π(121)
TSA = 2π(407)
TSA = 2,557.3 yd²
2) The total surface area is:
2(¹/₂ * 9 * 11.12) + (16 * 15) + (16 * 12) + (9 * 16)
= 25.02 + 240 + 192 + 144
= 601.02 m₂
3) The total surface area of a cylinder is:
2πrh + 2πr².
where:
r is radius
h is height
Thus:
TSA = 2π(14 * 29) + 2π(14)²
TSA = 2π(406) + 2π(196)
TSA = 2π(602)
TSA = 3782.5 mm²
4) The total surface area of the pyramid is:
TSA = (15 * 8) + (21 * 17) + (21 * 15) + (8 * 21)
TSA = 120 + 147 + 315 + 168
TSA = 750 in²
Read more about Total Surface Area at: https://brainly.com/question/27812847
#SPJ1
minimum of [tex]\frac{a}{b+c} + \frac{b}{c+a} + \sqrt{} \frac{2c}{a+b}[/tex]
Answers
The minimum of the given expression can be found to be 3 x ∛(√2).
How to find the minimum ?Use these inequalities to find the minimum of the given expression:
(a / (b + c)) + (b / (c + a)) + √(2c / (a + b)) ≥ (a / (√(bc))) + (b / (√(ac))) + √(2c / (√(ab)))
Now, simplify the expression:
(a / (√(bc))) + (b / (√(ac))) + √(2c / (√(ab))) = (√(a²/bc)) + (√(b²/ac)) + (√(2c²/ab))
Apply AM-GM inequality to the terms (√(a²/bc)), (√(b²/ac)), and (√(2c²/ab)):
AM = [(√(a²/bc)) + (√(b²/ac)) + (√(2c²/ab))] / 3 ≥ GM = ∛[(√(a²/bc)) * (√(b²/ac)) * (√(2c²/ab))]
The geometric mean (GM) is:
GM = ∛[(√(a²/bc)) x (√(b²/ac)) x (√(2c²/ab))]
GM = ∛(√(2a²b²c² / a²b²c²))
GM = ∛(√2)
Thus, the minimum of the given expression is:
= 3 x ∛(√2)
Find out more on minimum at https://brainly.com/question/30196594
#SPJ1
assume that arrivals occur according to a poisson process with an average of seven per hour. what is the probability that exactly two customers arrive in the two-hour period of time between a 2:00 p.m. and 4:00 p.m. (one continuous two-hour period)? b 1:00 p.m. and 2:00 p.m. or between 3:00 p.m. and 4:00 p.m. (two separate one-hour periods that total two hours)?
Answers
a) The probability that exactly two customers arrive between 2:00 p.m. and 4:00 p.m. is 0.0915 (or approximately 9.15%).
b) The probability of at least one customer arriving between 1:00 p.m. and 2:00 p.m. or between 3:00 p.m. and 4:00 p.m. is approximately 0.99999917.
For a Poisson process, the number of arrivals in a fixed time interval follows a Poisson distribution.
Let's denote the number of arrivals in a two-hour period as X.
Since the average number of arrivals per hour is 7, the average number of arrivals in a two-hour period is 14.
Therefore, we have λ = 14.
a) Probability of exactly 2 customers arriving between 2:00 p.m. and 4:00 p.m.:
Using the Poisson distribution formula, the probability of X arrivals in a two-hour period is:
[tex]P(X = x) = (e^{-\lambda} * \lambda^x) / x![/tex]
So, for X = 2, we have:
[tex]P(X = 2) = (e^{-14} * 14^2) / 2! = 0.0915[/tex] (rounded to four decimal places)
Therefore, the probability that exactly two customers arrive between 2:00 p.m. and 4:00 p.m. is 0.0915 (or approximately 9.15%).
b) Probability of at least one customer arriving between 1:00 p.m. and 2:00 p.m. or between 3:00 p.m. and 4:00 p.m.:
We can approach this problem by using the complementary probability. The complementary probability of at least one customer arriving in a two-hour period is the probability of no customers arriving in that period. Since the arrival rate is the same for each hour, we can divide the two-hour period into two one-hour periods and use the Poisson distribution formula for each period separately.
The probability of no customers arriving in a one-hour period with λ = 7 is:
[tex]P(X = 0) = (e^{-7}* 7^0) / 0! = 0.000911[/tex]
The probability of no customers arriving in a two-hour period is the product of the probabilities for each one-hour period:
P(no customers in two-hour period) = P(X = 0) * P(X = 0) = 0.000911 * 0.000911 = 8.30e-7
The complementary probability of at least one customer arriving in a two-hour period is:
P(at least one customer in two-hour period) = 1 - P(no customers in two-hour period) = 1 - 8.30e-7 = 0.99999917 (rounded to eight decimal places).
For similar question on probability.
https://brainly.com/question/29260334
#SPJ11
shawna is going out of town for the day, so she asks a friend to watch her 3 dogs. she wants to leave 12 of a pound of food for each dog. if a can of dog food has 0.75 pounds of food, how many cans should shawna leave?write your answer as a whole number, decimal, fraction, or mixed number. simplify any fractions.
Answers
Shawna wants to make sure her three dogs are fed and cared for when she leaves town for the day. She intends to give each of her dogs 12 ounces of food to achieve this. She must therefore leave a total of 36 ounces of food (3 dogs x 12 ounces of food per dog). 36 ounces are equivalent to 2.25 pounds of food because 16 ounces make up one pound.
There are 0.75 pounds of food in each can of dog food. We must divide 2.25 by 0.75 to find the quantity of dog food Shawna should leave for her companion. 3 dog food cans are the end outcome.Shawna ought to give her buddy three cans of dog food so that she can feed her dogs.
Shawna may make sure her dogs have enough food and are well cared for while she is away by leaving adequate food for them. Shawna may put any fears or concerns about her pets' welfare to rest by leaving ample food and clear directions.
Learn more about fractions:
https://brainly.com/question/10354322
Male mosquitos have pretty short lifespans. Males of a certain species have lifespans that are strongly skewed to the right with a mean of 8 88 days and a standard deviation of 6 66 days. A biologist collects a random sample of 36 3636 of these male mosquitos and observes them to calculate the sample mean lifespan. What is the probability that the mean lifespan from the sample of 36 3636 mosquitos x ˉ x ˉ x, with, \bar, on top exceeds 10 1010 days? Choose 1 answer: Choose 1 answer: (Choice A) A P ( x ˉ > 10 ) ≈ 0. 02 P( x ˉ >10)≈0. 02P, left parenthesis, x, with, \bar, on top, is greater than, 10, right parenthesis, approximately equals, 0, point, 02 (Choice B) B P ( x ˉ > 10 ) ≈ 0. 14 P( x ˉ >10)≈0. 14P, left parenthesis, x, with, \bar, on top, is greater than, 10, right parenthesis, approximately equals, 0, point, 14 (Choice C) C P ( x ˉ > 10 ) ≈ 0. 25 P( x ˉ >10)≈0. 25P, left parenthesis, x, with, \bar, on top, is greater than, 10, right parenthesis, approximately equals, 0, point, 25 (Choice D) D P ( x ˉ > 10 ) ≈ 0. 37 P( x ˉ >10)≈0. 37P, left parenthesis, x, with, \bar, on top, is greater than, 10, right parenthesis, approximately equals, 0, point, 37 (Choice E) E We cannot calculate this probability because the sampling distribution is not normal
Answers
Given a sample of 36 male mosquitos of a species with a mean lifespan of 8.88 days and a standard deviation of 6.66 days, the probability of the sample mean lifespan exceeding 10 days is approximately 0.14. So, the correct choice is option B is P ( x ˉ > 10 ) ≈ 0. 14 P( x ˉ >10)≈0. 14P, left parenthesis, x, with, \bar, on top, is greater than, 10, right parenthesis, approximately equals, 0, point, 14.
The sampling distribution of the mean lifespan is approximately normal due to the Central Limit Theorem.
The standard error of the mean is 6.66 / sqrt(36) = 1.11. The z-score for a sample mean of 10 is (10 - 8.88) / 1.11 = 1.08. Using a standard normal distribution table or calculator, the probability of a z-score greater than 1.08 is approximately 0.14.
Therefore, the answer is Choice B is P(X > 10) ≈ 0.14.
To know more about Probability:
https://brainly.com/question/11234923
#SPJ4
I need to know what to fill out
Answers
The function is a linear function because as x increases, the y-value changes at a constant rate . The rate of change of this equation is 2.
How to find linear functions?The difference between linear and exponential functions is that Linear functions change at a constant rate per unit interval while an exponential function changes by a common ratio over equal intervals.
We are given the function table as:
(0, -3)
(1, -1)
(2, 1)
(3, 3)
Thus, we can see that as x increases, the y-value changes at a constant rate of + 2.
Read more about Linear Functions at: https://brainly.com/question/15602982
#SPJ1
help please this is due tonight and im struggling
Answers
Thus, the value of x for the given angle of cyclic quadrilateral is found as the x = 50.
Explain about the cyclic quadrilateral:When you hear the word "cyclic," think of the two round wheels on you bicycle. A quadrilateral is a figure with four sides. The result is a cyclic quadrilateral, which is defined as any four-sided shape (quadrilateral) its four vertices (corners) are located on a circle.
A cyclic quadrilateral's opposite angles add up to 180 degrees, making them supplementary to one another.
Given data:
∠T = x + 60°∠R = x + 20°Using the property of cyclic quadrilateral: sum of opposite angle are 180 degrees.
∠T + ∠R = 180
x + 60 + x + 20 = 180
2x + 80 = 180
2x = 180 - 80
2x = 100
x = 50
Thus, the value of x for the given angle of cyclic quadrilateral is found as the x = 50.
Know more about the cyclic quadrilateral:
https://brainly.com/question/27585352
#SPJ1
2. when conducting a hypothesis test, the hypothesis that illustrates what we really think is going on in the population is called the hypothesis. an. analytical b. hypothetical c. null d. theoretical e. alternative
Answers
what is the degree of the polynomial 8 x to the power of 5 plus 4 x cubed minus 5 x squared minus 9 ?
Answers
Out of these powers, the highest is 5.
Therefore, the degree of the polynomial is 5.
The degree of a polynomial is the highest power of the variable in the polynomial. In the given polynomial, the highest power of x is 5,
so the degree of the polynomial is 5.
The degree of a polynomial is the highest power of the variable (x) in the expression.
In the polynomial you provided:
[tex]8x^5 + 4x^3 - 5x^2 - 9[/tex]
Let's identify the terms and their respective powers of x:
[tex]8x^5[/tex]has a power of 5.
[tex]4x^3[/tex]has a power of 3.
[tex]-5x^2[/tex] has a power of 2.
-9 is a constant term, so there is no power of x.
For similar question on polynomial.
https://brainly.com/question/24662212
#SPJ11
Simplify. 11 3/4-8 1/2
Answers
Therefore, 11 3/4 - 8 1/2 = 13/4, or 3 1/4 as a mixed number.
What is mixed number?A mixed number is a type of number that represents a whole number and a fraction together. It is written in the form of a whole number followed by a fraction, such as 3 1/2. The whole number represents the number of whole units, while the fraction represents the part of a unit.
For example, the mixed number 3 1/2 can be interpreted as three whole units and one half of a unit. Another example of a mixed number is 2 3/4, which represents two whole units and three-quarters of a unit. Mixed numbers are commonly used in everyday life, such as in cooking and measuring, and in mathematical calculations involving fractions.
To subtract mixed numbers like these, we need to convert them to improper fractions first:
[tex]11 3/4 = (4 * 11 + 3)/4 = 47/4[/tex]
[tex]8 1/2 = (2 * 8 + 1)/2 = 17/2[/tex]
Now, we can subtract the fractions:
[tex]47/4 - 17/2[/tex]
To subtract these fractions, we need to find a common denominator. The least common multiple of 4 and 2 is 4 × 2 = 8. We can convert both fractions to have a denominator of 8:
[tex]47/4 = (47/4) * (2/2) = 94/8[/tex]
[tex]17/2 = (17/2) * (4/4) = 68/8[/tex]
Now, we can subtract the numerators:
[tex]94/8 - 68/8 = 26/8[/tex]
Finally, we can simplify the result by dividing both numerator and denominator by their greatest common factor, which is 2:
[tex]26/8 = (2 * 13)/(2 * 4) = 13/4[/tex]
To know more about common factor, visit:
https://brainly.com/question/30961988
#SPJ1
please help someone..50 points
Answers
Answer:
We can find the sum of the interior angles of any polygon using the formula
[tex]S_{n}=180(n-2)[/tex], where n is the number of sides.
Because each of these polygons have four sides, we can use one formula where our n is 4 to find the sum of the interior angles:
[tex]S_{4}=180(4-2)\\ S_{4}=180*2\\ S_{4}=360[/tex]
Thus, for all four problems, we can set the four angles equal in the four polygons equal to 360 and solve for the variables
(15) *Note the right angle symbol in this problem which always equals 90°
[tex]84+90+(2x+118)+(2x+68)=360\\174+2x+118+2x+68=360\\360+4x=360\\4x=0\\x=0[/tex]
Now, to find the measure of <Y, we simply plug in 0 for x in its equation
m<Y = 2(0) + 118 = 118°
(16):
[tex]82+105+(8x+11)+10x=360\\187+8x+11+10x=360\\198+18x=360\\18x=162\\x=9[/tex]
To find the measure of <F, we plug in 9 for x in its equation
m<F = 10(9) = 90°
(17):
[tex]95+95+(10x-5)+(8x+13)=360\\190+10x-5+8x+13=360\\198+18x=360\\18x=162\\x=9[/tex]
To find the measure of <M, we plug in 9 for x in its equation
m<M = 10(9) - 5 = 85°
(18):
[tex](14x-7)+(11x-2)+93+76=360\\14x-7+11x-2+169=360\\25x+160=360\\25x=200\\x=8[/tex]
To find the measure of <M, we plug in 8 for x in its equation
m<M = 11(8) - 2 = 86°
Suppose an earthquake can be felt up to 76 miles from its epicenter. You are located at a point 65 miles west and 40 miles south of the epicenter. Do you feel the earthquake?
Answers
The distance between your location and the epicenter is just slightly larger than the maximum distance that the earthquake can be felt (76 miles), so you would be able to feel the earthquake.
What is triangle?A triangle is a polygon with three sides and three angles. The sum of the angles in a triangle is always 180 degrees. There are different types of triangles such as equilateral, isosceles, scalene, right-angled, obtuse-angled, and acute-angled triangles. Triangles are used in geometry and other fields of mathematics to solve problems related to areas, angles, and side lengths.
Here,
Yes, you feel the earthquake.
To see why, imagine drawing a circle around the epicenter with a radius of 76 miles. This circle represents the maximum distance that the earthquake can be felt. Then, draw a line from the epicenter to your location. This line represents the distance between you and the epicenter.
To determine whether you feel the earthquake, we need to calculate the distance between your location and the epicenter using the Pythagorean theorem:
distance = √(65² + 40²)
distance ≈ 76.06 miles
To know more about triangle,
https://brainly.com/question/28600396
#SPJ1
At Robinson’s Steakhouse, you can choose from 2 steaks cooked to your liking and have the choice of 2 different sides. What is the probability that a customer will choose a Ribeye, well done or medium with corn?
A- 1/3
B- 1/12
C- 2/7
D- 1/6
Answers
the probability of a customer choosing a Ribeye, well done or medium with corn is [tex]1[/tex] out of [tex]12[/tex], which is answer B [tex]- 1/12[/tex] Thus, option B is correct.
What is the probability?There are two possible steaks that a customer can choose from, and for each steak, there are three possible ways to cook it: rare, medium, or well-done. Additionally, there are two possible sides to choose from: corn or some other option.
Thus, there are a total of [tex]2 \times 3 \times 2 = 12[/tex] possible meal combinations that a customer can choose from.
Out of these 12 possibilities, there is only one way to get a Ribeye cooked well-done or medium with corn, since there is only one Ribeye option on the menu.
Therefore, the probability of a customer choosing a Ribeye, well done or medium with corn is 1 out of 12, which is answer B- 1/12
Learn more about probability here:
https://brainly.com/question/30034780
#SPJ1
a bag contains 7 red balls, 9 blue balls, and 4 yellow balls. what is the minimum number of balls that must be selected to ensure that 4 balls of the same color are chosen?
Answers
The number of balls that must be selected to ensure that 4 balls of the same color are chosen is 10 balls.
To ensure that 4 balls of the same color are chosen, we must consider the worst-case scenario where we select 3 balls of each color before selecting the fourth ball. Therefore, the minimum number of balls that must be selected is:
= 3 (red balls) + 3 (blue balls) + 3 (yellow balls) + 1 (any color)
= 10 balls.
Therefore, we must select at least 10 balls to ensure that 4 balls of the same color are chosen.
To know more about balls
https://brainly.com/question/19930452
#SPJ4