PLEASE HELP. Lesson 15.3 Tangents and Circumscribed Angles
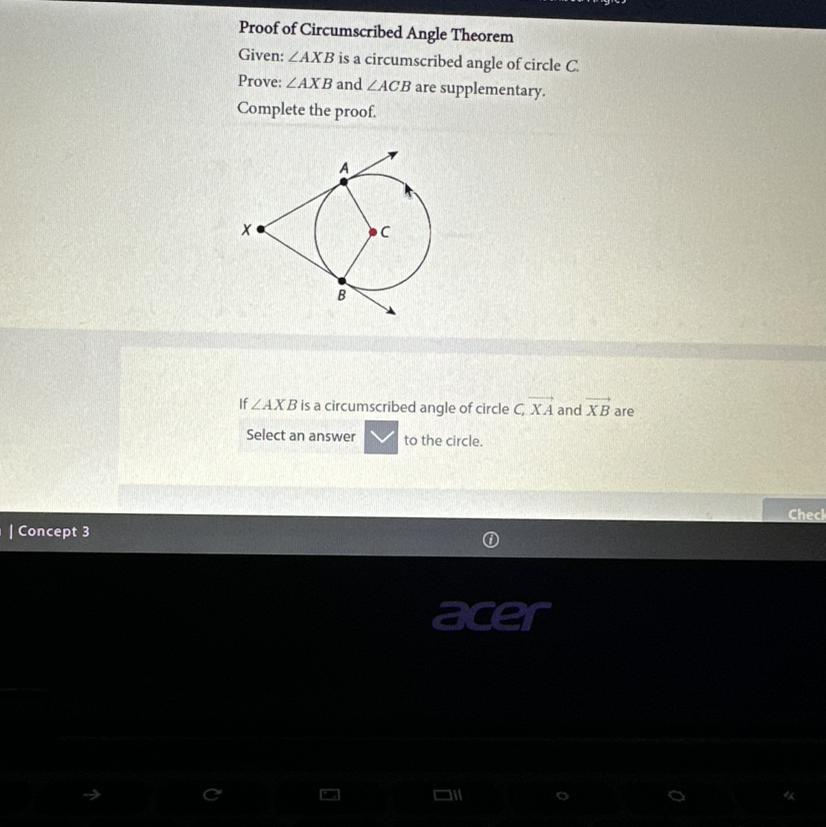
Proof of Circumscribed Angle Theorem
Given: ZAXB is a circumscribed angle of circle C.
Prove: ZAXB and ZACB are supplementary.
Complete the proof.
A
B
C
If ZAXB is a circumscribed angle of circle C, XA and XB are
Select an answer to the circle

The NPV of the CBCS project, using an 8% discount rate, is. [tex]\$21,646.77.[/tex]

Financial value proposition of CBCS:

The financial value proposition of CBCS is based on several factors:

Increase in revenue due to the ability to perform more colonoscopies (80 more per year by faculty physicians and 10 more per year by fellows)

Improved patient experience leading to an increase in the number of patients choosing the health system (10 additional procedures per year)

Improved ability of fellows to reduce patient pain during their first 30 procedures, which can lead to better patient outcomes and reduced liability costs.

Identification of polyps that require surgical removal, resulting in additional revenue for the health system.

Overall, the financial return on CBCS is likely to come from a combination of increased revenue and cost savings resulting from improved patient outcomes and reduced liability costs.

Financial analysis in Excel:

Please see attached Excel file for the financial analysis.

IRR calculation:

The IRR of the CBCS project is 23.2%.

Payback period calculation:

The payback period of the CBCS project is 2.6 years.

CBCS project is 2.6 years.

For similar questions on discount rate.

https://brainly.com/question/13660799

#SPJ11

So the radius and diameter for each plate are:

Plate 1: radius ≈ 7 in., diameter ≈ 14 in.

Plate 2: radius ≈ 4.5 in., diameter ≈ 9 in.

Plate 3: radius ≈ 3.5 in., diameter ≈ 7 in.

Circumference is the distance around the edge of a circle. It is the total length of the boundary of a circle. It is also referred to as the perimeter of a circle. The circumference of a circle can be calculated using the formula: C = 2πr where C is the circumference, r is the radius of the circle, and π is a mathematical constant with an approximate value of 3.14. The circumference of a circle is directly proportional to its radius; that is, as the radius of a circle increases, the circumference also increases.

Here,

Part A:

To find the radius and diameter of each plate, we can use the formula for the circumference of a circle:

C = 2πr

where C is the circumference and r is the radius. We can rearrange this formula to solve for the radius:

r = C / 2π

Using the given circumferences and the value of π as 3.14, we can find the radius for each plate:

Plate 1:

C = 43.96 in.

r = 43.96 / (2 x 3.14) ≈ 7 in.

d = 2r ≈ 14 in.

Plate 2:

C = 28.26 in.

r = 28.26 / (2 x 3.14) ≈ 4.5 in.

d = 2r ≈ 9 in.

Plate 3:

C = 21.98 in.

r = 21.98 / (2 x 3.14) ≈ 3.5 in.

d = 2r ≈ 7 in.

So the radius and diameter for each plate are:

Plate 1: radius ≈ 7 in., diameter ≈ 14 in.

Plate 2: radius ≈ 4.5 in., diameter ≈ 9 in.

Plate 3: radius ≈ 3.5 in., diameter ≈ 7 in.

Part B:

To find the radius and diameter of each plate, we used the formula for the circumference of a circle and rearranged it to solve for the radius. We then used the formula for the diameter of a circle, which is simply twice the radius, to find the diameter. We also used the value of π as 3.14 in our calculations.

To know more about circumference,

https://brainly.com/question/11213974

#SPJ1

Answer:

[tex]\dfrac{4}{3}[/tex]

Step-by-step explanation:

We can find the y-intercept of this line by:

1) finding the slope using the given points

[tex]m = \dfrac{8-(-7)}{4-(5)}[/tex]

[tex]m = \dfrac{8+7}{4+5}[/tex]

[tex]m = \dfrac{15}{9}[/tex]

[tex]m=\dfrac{5}{3}[/tex]

2) forming an equation for the line using point slope form

[tex]y - b = m(x - a)[/tex]     where [tex](a,b)[/tex] is a point on the line

... using the point (4,8)

[tex]y - 8 = \frac{5}{3}(x - 4)[/tex]

3) plugging 0 in for x to get the y-intercept

[tex]y - 8 = \frac{5}{3}(0 - 4)[/tex]

[tex]y - 8 = \frac{5}{3}(-4)[/tex]

[tex]y = 8 -\frac{20}{3}[/tex]

[tex]y = \frac{24}{3} -\frac{20}{3}[/tex]

[tex]\boxed{y=\dfrac{4}{3}}[/tex]

The researcher should consider the following steps when creating the two groups: Random assignment, Pairing students with similar abilities, Controlling for potential confounding variables,

Collecting data and analyzing results.
Random assignment:

To minimize any potential bias, the researcher should randomly assign one student from each pair to receive extra homework problems while the other does not.
Pairing students with similar abilities:

In order to make a valid comparison, the researcher should pair students with similar algebra skills or previous performance in the subject.

This way, any observed differences in the test results are more likely to be due to the extra homework rather than differences in ability.
Controlling for potential confounding variables:

The researcher should control for any other factors that could influence students' algebra test results, such as attendance, study habits, and teacher quality.

After the two-week period, the researcher should collect the test scores of both groups and compare their performance.

This can be done using statistical methods, such as a paired t-test, to determine if there is a significant difference between the groups.

For similar question on researcher.

https://brainly.com/question/30106546

#SPJ11

(a) The linear density (mass/length) rho has SI units of kg/m. Since rho = a + bx, the SI units of a must be kg/m and the SI units of b must be kg/m^2.
(b) To find the mass of the rod, we need to integrate the linear density function over the length of the rod:
m = ∫₀ᴸ ρ(x) dx
Substituting in ρ(x) = a + bx:
m = ∫₀ᴸ (a + bx) dx
m = [ax + (1/2)bx²] from 0 to L
m = aL + (1/2)bL²
Therefore, the mass of the rod in terms of a, b, and L is m = aL + (1/2)bL².

(a) In this problem, rho (ρ) represents linear density, which has units of mass per length. In SI units, mass is measured in kilograms (kg) and length in meters (m). Therefore, the units of linear density are kg/m. Since ρ = a + bx, the units of a and b must be consistent with this equation. The units of a are the same as those of ρ, so a has units of kg/m. For b, since it is multiplied by x (which has units of meters), b must have units of kg/m² to maintain consistency in the equation.

(b) To find the mass of the rod, we need to integrate the linear density function over the length of the rod (from x=0 to x=L). Let's set up the integral:

Mass (M) = ∫(a + bx) dx, with limits from 0 to L

Now, we can integrate:

M = [a * x + (b/2) * x²] evaluated from 0 to L

Substitute the limits:

M = a * L + (b/2) * L²

So, the mass of the rod in terms of a, b, and L is:

M = aL + (bL²)/2

To learn more about density visit;

https://brainly.com/question/29775886

#SPJ11

(b) The volume of the medium box is 5832 cubic inches.

In mathematics, a ratio is a comparison of two quantities or numbers. It is expressed as the quotient of one number divided by another, and is often written as "a:b" or "a/b". Ratios are used to compare the sizes of two or more quantities, and they can be used to solve problems involving proportions and percentages.

For example, if a recipe calls for a ratio of 2 cups of flour to 1 cup of sugar, this means that for every 2 cups of flour used, 1 cup of sugar should be used as well. Similarly, if a company has a debt-to-equity ratio of 2:1, this means that for every $2 of debt, the company has $1 of equity.

(a) Let x be the length of the sides of the original box. Then the volume of the box is x^3 = 216, so x = 6.

When the length, width, and height are all tripled, the new side length of the medium box is 3x = 18.

The ratio of the sides of the medium box to the original box is 18:6, or simplified, 3:1.

The area of the base of the original box is. [tex]x^2 = 6^2 = 36[/tex]square inches.

The area of the base of the medium box is. [tex](3x)^2 = 18^2 = 324[/tex] square inches.

The ratio of the 5832 of the bases of the medium box to the original box is 324:36, or simplified, 9:1.

The volume of the medium box is. [tex](3x)^3 = 18^3 = 5832[/tex]cubic inches.

The ratio of the volumes of the medium box to the original box is 5832:216, or simplified, 27:1.

(b) The volume of the medium box is 5832 cubic inches.

To know more about volume visit:

https://brainly.com/question/13338592

#SPJ1

The volume of the sphere with a radius of 7 feet is therefore 1436.8 cubic feet when expressed in terms of pi and rounded to the closest tenth (or about 1436.76 cubic feet).

The volume of such a three-dimensional object is the amount of space it takes up in algebra and geometry. It is a description of an object's capacity and, depending on the situation, may be stated in terms of cubic metres, cubic centimetres, litres, or gallons. A cube's volume, for instance, can be determined by adding up its length, width, and height. An equation for calculating a cube's volume is: V = l × w × h where V indicates for volume, l for length, w for width, and h for height.

given

The following equation determines a sphere's volume:

[tex]V = (4/3)\pi r^3[/tex]

where r denotes the sphere's radius.

If we substitute r = 7 feet, we obtain:

[tex]V = (4/3)\pi (7 feet)^3[/tex]

Using V, 1436.76 cubic feet (3.14159)

To the nearest tenth, we round and obtain:

1436.8 cubic feet equals V.

The volume of the sphere with a radius of 7 feet is therefore 1436.8 cubic feet when expressed in terms of pi and rounded to the closest tenth (or about 1436.76 cubic feet).

To know more about volume visit :-

https://brainly.com/question/1578538

#SPJ1

The Gabrielsons ran a total of 30 kilometers in the family relay race.

What is the equivalent expression?

Equivalent expressions are expressions that perform the same function despite their appearance. If two algebraic expressions are equivalent, they have the same value when we use the same variable value.

It seems that there are five family members who participated in the relay race, and the distance run by each of them in kilometers is listed as follows:

11, 4, 8, 2, 5

To find the total distance run by the family, we simply add up the distances:

11 + 4 + 8 + 2 + 5 = 30

Therefore, the Gabrielsons ran a total of 30 kilometers in the family relay race.

To learn more about the equivalent expression visit:

https://brainly.com/question/2972832

#SPJ1

a) The graph for the function [tex]A = 225 - 3.14r^2[/tex] is a downward sloping parabola.

b) The x-values make sense for the domain is a non-negative number.

c) The y-values make sense for the range is  0≤ A≤ 25.

In mathematics, a graph is a collection of points, called vertices or nodes, and edges that connect pairs of vertices.

a. To graph the function [tex]A = 225 - 3.14r^2[/tex]. The graph should be a downward-sloping parabola, opening downwards.

b. The domain of the function represents the possible values of r. Since the radius of a circle cannot be negative, the x-values (or the values of r) that make sense for the domain are non-negative numbers, i.e., r >= 0.

c. The range of the function represents the possible values of A, the area to be painted blue. Since the poster board is 15 in wide, the maximum area that can be painted blue is 225 sq in (15 in x 15 in). Since the area of the circular drawing is given by [tex]3.14r^2[/tex], the area to be painted blue can be no greater than 225 sq in, which occurs when the circular drawing has a radius of 0. Therefore, the y-values (or the values of A) that make sense for the range are 0 <= A <= 225.

To know more about graph visit:

https://brainly.com/question/19040584

#SPJ1

Therefore, the probability of exactly 5 cars arriving over a 5-minute interval during rush hour is approximately 0.017 or 1.7%.

To solve this problem, we first need to determine the rate of cars arriving per minute. We can do this by dividing 25 cars by 11 minutes, which gives us a rate of approximately 2.27 cars per minute.

Next, we need to use the Poisson distribution formula to calculate the probability of exactly 5 cars arriving over a 5-minute interval. The Poisson distribution is used to model the probability of a certain number of events occurring within a given time frame when those events occur randomly and independently of each other.

The formula for the Poisson distribution is:

[tex]P(X = k) = (e^-lambda * lambda^k) / k![/tex]

Where:
- P(X = k) is the probability of k events occurring within the specified time frame
- e is Euler's number (approximately equal to 2.718)
- λ is the average rate of events occurring per unit of time (in our case, 2.27 cars per minute)
- k is the number of events we want to calculate the probability for
- k! is the factorial of k (i.e., k! = k * (k-1) * (k-2) * ... * 2 * 1)

Plugging in the values we have, we get:

[tex]P(X = 5) = (e^-2.27 * 2.27^5) / 5![/tex]
P(X = 5) = (0.040 * 51.84) / 120
P(X = 5) = 0.017

Therefore, the probability of exactly 5 cars arriving over a 5-minute interval during rush hour is approximately 0.017 or 1.7%.

Learn more about probability here:

https://brainly.com/question/30034780

#SPJ11

The probability that exactly five cars will arrive over a 5-minute interval during rush hour is approximately 0.0126 or 1.26%.

To solve this problem, we will use the Poisson distribution formula.

Calculate the average arrival rate (λ) for a 5-minute interval.
Since 25 cars arrive in 11 minutes, we can find the rate per minute as follows:
(25 cars) / (11 minutes) ≈ 2.27 cars per minute
For a 5-minute interval, multiply the rate per minute by 5:
(2.27 cars per minute) × (5 minutes) ≈ 11.36 cars.

Use the Poisson distribution formula to find the probability.
The Poisson distribution formula is:
[tex]P(x) = (e^{-\lambda} *  (\lambda^x)) / x![/tex]
In this problem, x = 5 (exactly five cars) and λ ≈ 11.36.
Calculate the probability.
P(5) = (e^(-11.36) × (11.36^5)) / 5!
P(5) ≈ 0.0126.

For similar question on probability.

https://brainly.com/question/30075981

#SPJ11

Answer:

BC=4

AC=[tex]4\sqrt{2}[/tex]

Answer:

k = - 8

Step-by-step explanation:

given that (x - a) is a factor of f(x) , then f(a) = 0

given

(x - 1) is a factor of f(x) then f(1) = 0 , that is

3(1)³ + 5(1) + k = 0

3(1) + 5 + k = 0

3 + 5 + k = 0

8 + k = 0 ( subtract 8 from both sides )

k = - 8

There are 302,702,400 possible baseball teams of nine that can be formed with three designated pitchers and 12 multitalented players who can play any of the remaining positions.

Since three players are designated as pitchers, we need to choose three players out of the total 15 players on the team. This can be done in C(15, 3) ways, where C(n, r) represents the number of combinations of r objects selected from a set of n objects.

For the remaining six positions, any of the 12 multitalented players can be assigned to any of the positions, which means that there are 12 choices for the first position, 11 choices for the second position, and so on, down to 7 choices for the sixth position.

Therefore, the total number of baseball teams of nine that can be formed is:

C(15, 3) x 12 x 11 x 10 x 9 x 8 x 7

which simplifies to:

(15 x 14 x 13 / 3 x 2 x 1) x (12 x 11 x 10 x 9 x 8 x 7)

= 455 x 665,280

= 302,702,400

To learn more about combinations click on,

https://brainly.com/question/27511977

#SPJ4

The flour will fit into two of the container is 144 inches.

What is the volume of cuboids?

A cuboid is a six-sided solid known as a hexahedron. Quadrilaterals make up its faces. Cuboid is short for "like a cube". A cuboid is similar to a cube in that a cuboid can become a cube by varying the lengths of the edges or the angles between the faces.

Here, we have

Given: Mrs. Hanson is filling containers in her bakery with flour.

we have to find how much flour will fit into two of the containers.

Volume of cuboid = length × breadth × height

Length = 6 inches

Breadth = 3 inches

Height = 8 inches

The flour will fit into two of the containers = length × breadth × height

= 6 ×3 × 8

= 144 inches

Hence, The flour will fit into two of the container 144 inches.

To learn more about the volume of cuboids from the given link

https://brainly.com/question/30176305

#SPJ1

Probability about at least one customer arrives at the shop while a one-minute interval is almost 0.632 or 63.2%.

The probability that at least one customer arrives at the shop during a one-minute interval can be calculated using the Poisson distribution, which is commonly used to model the arrival of events over a given time period.

Let's assume that the average number of customers arriving at the shop per minute is [tex]l[/tex]. Poisson probability mass function is;

[tex]P(X = k) = (e^{-l} * l^k) / k![/tex]

where X is the random variable representing the number of customers arriving in a one-minute interval, and k is the number of customers that arrive.

To find the probability of at least one customer arriving, we need to calculate the probability of X being greater than or equal to 1. That is,

[tex]P(X > = 1) = 1 - P(X = 0)[/tex]

When [tex]l[/tex] is relatively small, we can use approximation:

[tex]P(X = 0) = e^{-l[/tex]

Therefore,

[tex]P(X > = 1) = 1 - P(X = 0)[/tex]

[tex]≈ 1 - e^{-l[/tex]

We don't have the value of [tex]l[/tex], but assuming an average arrival rate of 1 customer per minute (i.e., [tex]l[/tex] = 1), we get:

[tex]P(X > = 1) = 1 - e^{-1[/tex]

≈ 0.632

Therefore, the probability about  at least one customer arrives at the shop while a one-minute interval is almost 0.632 or 63.2%.

Learn more about Probability.

brainly.com/question/30034780

#SPJ11

The ratio of 2:3:30 in 385​ can be expressed with the values 22:33:330 repectively.

To find the actual values represented by the ratio 2:3:30 in 385, we need to first add up the parts of the ratio: 2 + 3 + 30 = 35.

Next, we can find the value of each "part" of the ratio by dividing the total value (385) by the total number of parts (35):

385 ÷ 35 = 11

Now we can multiply each part of the ratio by this value to find the actual values:

2 x 11 = 22

3 x 11 = 33

30 x 11 = 330

So the ratio 2:3:30 in 385 represents the values 22:33:330.

Learn more about ratio at:

https://brainly.com/question/12024093

#SPJ1

The equivalent sum to the given equation is -9c - 20.

An algebraic expression is consists of variables, numbers with various mathematical operations.

Equivalent sums refers to addition or subtraction from the other number to maintain the same total value.

= 9c-12-15c-8-3c

To find the equivalent sum, first we can simplify this expression by first combining like terms:

= 9c - 15c - 3c - 12 - 8

= (9c - 15c - 3c) - (12 + 8)   (grouping the like terms)

Solving the expression for terms c and  for constant terms,

= -9c - 20

Therefore, the equivalent sum is -9c - 20.

To know more about algebraic expression

https://brainly.com/question/19245500

#SPJ4

Answer:

I dont know the answer to be honest..

JUST KIDDING.. ill answer this step by step lol

To solve the inequality 9/x + 81 > 45, we can follow these steps:

Step 1: Subtract 81 from both sides of the inequality to isolate the fraction on the left-hand side:

9/x + 81 - 81 > 45 - 81

9/x > -36

Step 2: Take the reciprocal of both sides of the inequality to eliminate the fraction:

1 / (9/x) < 1 / (-36)

x/9 < -1/36

Step 3: Multiply both sides of the inequality by 9 to get rid of the fraction in the numerator:

9 * (x/9) < 9 * (-1/36)

x < -1/4

So, the solution to the inequality 9/x + 81 > 45 is x < -1/4. This means that x must be less than -1/4 for the inequality to be true.

Answer:

63.3%

Step-by-step explanation:

30 divided by 100 and then multiplied by 19 gives u the answer

Answer:

8 pounds

Step-by-step explanation:

Simply add the fractions. Think of mixed fractions as whole numbers + fractions.

[tex]4\frac{1}{4} =\\4+\frac{1}{4} \\\\\\3\frac{3}{4} =\\3+\frac{3}{4}[/tex]

Now, add all the terms together:

[tex]4+\frac{1}{4}+3+\frac{3}{4} =\\\\ 7+\frac{4}{4}[/tex]

4/4 can be rewritten as 1, so we have:

[tex]7+\frac{4}{4} =\\\\ 7+1= \\\\8[/tex]

Thus, Sarah and Nathan picked 8 pounds of strawberries altogether.

An analysis of future events performed by the probability of those events and the potential outcomes is called probabilistic analysis.

Probabilistic analysis involves using mathematical models and statistical techniques to estimate the likelihood of different outcomes, given a set of assumptions and inputs. It is commonly used in risk management, financial analysis, and project management to evaluate the potential impact of different scenarios and make informed decisions. By quantifying the probabilities of different outcomes, probabilistic analysis helps decision-makers identify the best course of action and manage uncertainty and risk.

Learn more about probability

https://brainly.com/question/24756209

#SPJ4

Step-by-step explanation:

Ok do what you need to do is label the line opposite the square angle as H for the hypotenuse. Then label the line opposite the circular angle as O for the opposite. And finally, the last line remaining should be labelled as A for Adjacent. Does this help?

The process of bisecting an angle with a straightedge and compass is an important process in geometry. It is used to prove theorems, construct regular polygons, and much more. With enough practice, anyone can perfect this process and use it to their advantage.

Angle is a mathematical concept that describes the relationship between two lines (or edges) that share a common point (or vertex). It is measured in degrees, with a full circle being equal to 360 degrees. Angles can be either acute (less than 90 degrees), right (equal to 90 degrees), obtuse (greater than 90 but less than 180 degrees), or straight (equal to 180 degrees). Angles can also be classified as complementary (two angles whose sum equals 90 degrees) or supplementary (two angles whose sum equals 180 degrees).

1. Draw two rays from the vertex of the angle, and label them A and B.

2. Place the compass at A and draw an arc that intersects both rays.

3. Place the compass at B and draw an arc that intersects both rays.

4. The two arcs intersect at the bisector of the angle.

Bisecting an angle with a straightedge and compass is a simple process, but requires some practice to perfect. The process of bisecting an angle can be used to prove theorems in geometry, such as the Angle Bisector Theorem, which states that the bisector of an angle divides it into two congruent angles. This theorem can be used to prove the equality of two angles, or to construct an angle with a given measure.

Bisecting an angle can also be used to construct regular polygons, such as a hexagon. To construct a regular hexagon, one can use the process of bisecting an angle to construct six congruent angles. These angles can then be connected to form the sides of the hexagon.

The process of bisecting an angle with a straightedge and compass is an important process in geometry. It is used to prove theorems, construct regular polygons, and much more. With enough practice, anyone can perfect this process and use it to their advantage.

To know more about angle click-
https://brainly.com/question/25716982
#SPJ1

The value of the test statistic is approximately 2.84. Its significance can't be determined.

To determine whether or not there is a significant difference between the hourly wages of two companies, we need to conduct a hypothesis test.

The null hypothesis states that there is no significant difference between the hourly wages of the two companies, while the alternative hypothesis states that there is a significant difference.

The test statistic for this hypothesis test is calculated using the formula:

[tex]t = (x1 - x2) / (s1^2/n1 + s2^2/n2)^(1/2)[/tex]

where x1, x2 are the sample means for companies A and B, s1 and s2 are the sample standard deviations for companies A and B, and n1 and n2 are the sample sizes for companies A and B.

Plugging in given values, we get:

[tex]t = (6.75 - 6.25) / [(1^2/80) + (0.95^2/60)]^(1/2)[/tex]

t = 0.5 / 0.1759

t = 2.8437

Without knowing the significance level or the degrees of freedom, we cannot determine whether or not the test statistic is statistically significant.

Learn more about test statistic here:

https://brainly.com/question/14128303

#SPJ11

The value of the test statistic is 2.75.

To determine the test statistic for comparing the hourly wages of two companies, the researcher would need to conduct a two-sample t-test with equal variances.

The formula for the test statistic is:

[tex]t = (\bar x1 - \barx2) / [s_p \times \sqrt(1/n1 + 1/n2)][/tex]

where:

[tex]\bar x1[/tex] and[tex]\bar x2[/tex] are the sample means for Company A and Company B, respectively

[tex]s_p[/tex] is the pooled standard deviation of the two samples, calculated as:

[tex]s_p = sqrt [((n1 - 1) \times s1^2 + (n2 - 1) \times s2^2) / (n1 + n2 - 2)][/tex]

n1 and n2 are the sample sizes for Company A and Company B, respectively

s1 and s2 are the sample standard deviations for Company A and Company B, respectively.

Plugging in the given values, we get:

[tex]t = (6.75 - 6.25) / [\sqrt(((80-1)\times 1^2 + (60-1)\times 0.95^2)/(80+60-2)) \times \sqrt(1/80 + 1/60)][/tex]

[tex]t = 2.75[/tex]

For similar questions on statistic

https://brainly.com/question/15525560

#SPJ11

Answer:

it A or B

Step-by-step explanation:

the other two C and D dont make sense to what the question is asking

The ratio of their surface areas is x^2

Let's assume that the lengths of the edges of the first cube are a, and the lengths of the edges of the second cube are bx, where b is a constant.

The surface area of a cube is given by the formula A = 6a^2, where a is the length of an edge.

Therefore, the surface area of the first cube is 6a^2 and the surface area of the second cube is 6(bx)^2 = 6b^2x^2.

The ratio of their surface areas is:

(6b^2x^2) / (6a^2) = b^2x^2 / a^2

Since the ratio of the lengths of the edges of the two cubes is x, we have:

a / bx = 1 / x

Solving for a, we get:

a = bx^2

Substituting this value into the ratio of their surface areas, we get:

(b^2x^2) / (bx^2)^2 = (b^2x^2) / b^2x^4 = x^2

Therefore, the ratio of the surface areas of the two cubes is x^2.

Read more about surface area at

https://brainly.com/question/16519513

#SPJ1

Answer:

5 units is the distance

Step-by-step explanation:

7,2 is point c

7,7 is point d

7 - 7 = 0

7 - 2 = 5

5 is the answer

There are 19 people who own a cat or a dog.

A number is a mathematical object used to represent quantity, measurement, or a count of something. It can be an integer (whole number), a rational number (fraction), an irrational number (such as pi), or a real number (which includes all rational and irrational numbers).

To find the number of people who own a cat or a dog, we need to add the number of people who own only cats to the number of people who own only dogs, and then add the number of people who own both cats and dogs.

Let's start by finding the number of people who own only cats. We know that 16 people own cats, and 5 people own both cats and dogs. Therefore, the number of people who own only cats is:

16 - 5 = 11

Next, let's find the number of people who own only dogs. We know that 8 people own dogs, and 5 people own both cats and dogs. Therefore, the number of people who own only dogs is:

8 - 5 = 3

Finally, we can add the number of people who own only cats to the number of people who own only dogs, and then add the number of people who own both cats and dogs:

11 + 3 + 5 = 19

So, there are 19 people who own a cat or a dog.

Learn more about integer here:

https://brainly.com/question/15276410

#SPJ1

The correct answer is option b. Burger Quick, because it has a larger mean.

Statistics is a branch of mathematics that deals with the collection, analysis, interpretation, presentation, and organization of data. It involves using mathematical and computational methods to gather, analyze, and interpret data from various fields, including business, economics, medicine, engineering, psychology, and social sciences. Statistics allows researchers and analysts to draw conclusions and make predictions based on data, and is used in a wide range of applications, from designing experiments and conducting surveys to testing hypotheses and making decisions based on data-driven insights.

Burger Quick typically has more wait time, because it has a larger interquartile range (IQR) and a larger upper whisker on the box plot, indicating that there is more variability in the wait times and some customers have experienced longer wait times. Although the median wait time for Burger Quick is also larger, it is the IQR and upper whisker that provide more evidence for the longer wait times. The mean is not shown on the box plot and therefore cannot be used to determine which drive-thru typically has more wait time.

Therefore, the correct answer is option b. Burger Quick, because it has a larger mean.

To learn more about median from the given link

https://brainly.com/question/14532771

#SPJ1

$2,560 needs to be invested at time 3 in order to have $3,200 at time 8.

Since the money grows according to the simple interest accumulation function a(t) = 1.05t, the amount of money A at time t, given an initial amount P, can be calculated using the formula:

A = P + Pr(t)

where r is the interest rate (in this case, 5% or 0.05) and t is the time period (measured in years).

To determine how much money needs to be invested at time 3 to have $3,200 at time 8, we can use the above formula and solve for P:

3200 = P + Pr(8-3)

3200 = P + 5P(0.05)

3200 = P + 0.25P

3200 = 1.25P

P = 3200 / 1.25

P = 2560

Therefore, an initial investment of $2,560 at time 3 would be needed to have $3,200 at time 8, assuming a simple interest accumulation function with an interest rate of 5%.

Learn more about simple interest;

https://brainly.com/question/25845758

#SPJ4