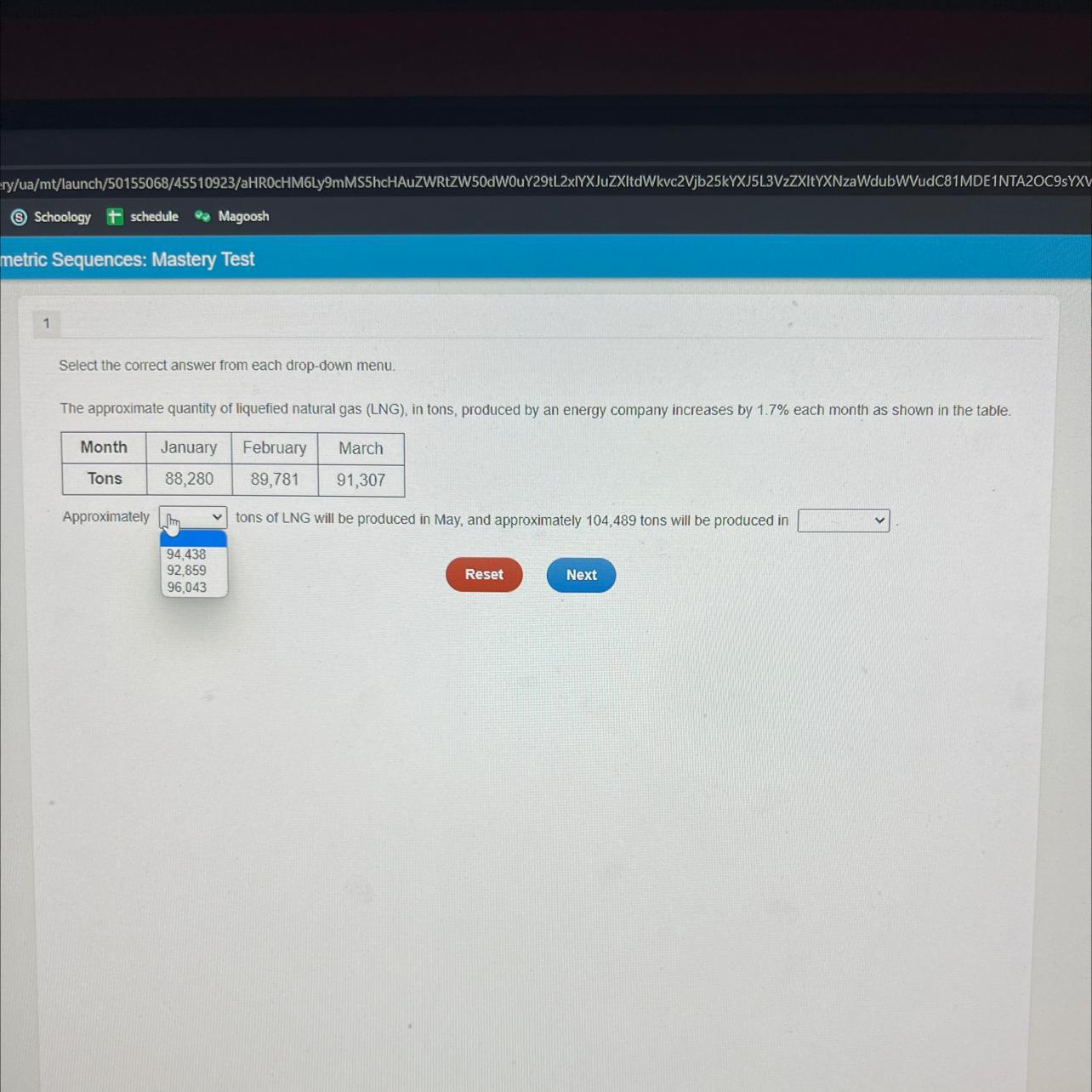
Select the correct answer from each drop-down menu.
The approximate quantity of liquefied natural gas (LNG), in tons, produced by an energy company increases by 1.7% each month as shown in the table.
January
88,280
Month
Tons
Approximately
February
March
89,781
91,307
tons of LNG will be produced in May, and approximately 104,489 tons will be produced in
Answers
Approximately 94,358 tons of LNG will be produced in May based on the given 1.7% monthly increase.
The given problem states that the approximate quantity of liquefied natural gas (LNG) produced by an energy company increases by 1.7% each month. We are given the production numbers for January, February, and March, and we need to calculate the approximate production for May.
To solve this problem, we can start with the production quantity in January, which is given as 88,280 tons. We then apply a 1.7% increase each month to find the production for subsequent months.
In February, the production can be calculated by multiplying the previous month's production by 1.017 (1 + 1.7%):
February production = 88,280 * 1.017 = 89,781 tons (rounded to the nearest whole ton).
Similarly, for March, we multiply the February production by 1.017:
March production = 89,781 * 1.017 = 91,307 tons (rounded to the nearest whole ton).
To find the production for May, we continue the pattern of applying a 1.7% increase:
April production = March production * 1.017 = 91,307 * 1.017 = 92,823 tons (rounded to the nearest whole ton).
Finally, we calculate the May production using the same method:
May production = April production * 1.017 = 92,823 * 1.017 = 94,358 tons (rounded to the nearest whole ton).
For more such information on: LNG
https://brainly.com/question/32004778
#SPJ8
Related Questions
The velocity v(t) in the table below is increasing for 0 t 12. Find an upper estimate for the total distance traveled using n = 4 subdivisions: distance traveled = n = 2 subdivisions: distance traveled = Which of the two answers in part (A) is more accurate? n = is more accurate (Be sure that you can explain why!) Find a lower estimate for the total distance traveled using n = 4. distance traveled =
Answers
Given: A table of velocity values. Let us find an upper estimate for the total distance traveled using n = 4 subdivisions and n = 2 subdivisions.The table of velocity values is shown below.
The formula for distance traveled is given by:$\Delta x=\sum_{i=1}^n v(t_i)\Delta t$The upper estimate for the total distance traveled using n = 4 subdivisions is:Distance traveled $= \Delta x = \sum_{i=1}^4 v(t_i) \Delta t$Here, $\Delta t = \dfrac{12-0}{4}=3$.Let us now substitute the values of velocity in the above formula.$\Delta x = v(0)3 + v(3)3 + v(6)3 + v(9)3 + v(12)3$$\Delta x = 0(3) + 3(3) + 9(3) + 15(3) + 21(3)$$\Delta x = 0 + 27 + 81 + 135 + 189$$\Delta x = 432$The upper estimate for the total distance traveled using n = 4 subdivisions is 432.The distance traveled using n = 2 subdivisions is:$\Delta x = \sum_{i=1}^2 v(t_i) \Delta t$Here, $\Delta t = \dfrac{12-0}{2}=6$.Let us now substitute the values of velocity in the above formula.$\Delta x = v(0)6 + v(6)6 + v(12)6$$\Delta x = 0(6) + 9(6) + 21(6)$$\Delta x = 0 + 54 + 126$$\Delta x = 180$Which of the two answers in part (A) is more accurate?Answer: n = 4 is more accurate than n = 2. Because, if we use more subdivisions, it gives us a better estimate. In other words, as n increases, the accuracy of our estimate increases.The lower estimate for the total distance traveled using n = 4 is:$\Delta x = \sum_{i=1}^4 v(t_i) \Delta t$Here, $\Delta t = \dfrac{12-0}{4}=3$.Let us now use the lower estimate and substitute the minimum value of velocity in the formula.$\Delta x = v(0)3 + v(3)3 + v(6)3 + v(9)3 + v(12)3$$\Delta x = 0(3) + 3(3) + 6(3) + 9(3) + 12(3)$$\Delta x = 0 + 9 + 18 + 27 + 36$$\Delta x = 90$Hence, the lower estimate for the total distance traveled using n = 4 is 90.
to know more about velocity visit:
https://brainly.in/question/11504533
#SPJ11
The velocity v(t) in the table below is increasing for 0 t 12. The lower estimate for the total distance traveled using n = 4 is 90.
Given: A table of velocity values. Let us find an upper estimate for the total distance traveled using n = 4 subdivisions and n = 2 subdivisions.
The formula for distance traveled is given by:[tex]$\Delta x=\sum_{i=1}^n v(t_i)\Delta t$[/tex].
The upper estimate for the total distance traveled using n = 4 subdivisions is: Distance traveled [tex]$= \Delta x = \sum_{i=1}^4 v(t_i) \Delta t$[/tex].
Here, [tex]$\Delta t = \dfrac{12-0}{4}=3$[/tex].
Let us now substitute the values of velocity in the above formula.
[tex]$\Delta x = v(0)3 + v(3)3 + v(6)3 + v(9)3 + v(12)3$$\Delta x = 0(3) + 3(3) + 9(3) + 15(3) + 21(3)$$\Delta x = 0 + 27 + 81 + 135 + 189$$\Delta x = 432$[/tex]The upper estimate for the total distance traveled using n = 4 subdivisions is 432.
The distance traveled using n = 2 subdivisions is: [tex]$\Delta x = \sum_{i=1}^2 v(t_i) \Delta t$[/tex]
Here, [tex]$\Delta t = \dfrac{12-0}{2}=6$.[/tex]
Let us now substitute the values of velocity in the above formula.[tex]$\Delta x = v(0)6 + v(6)6 + v(12)6$$\Delta x = 0(6) + 9(6) + 21(6)$$\Delta x = 0 + 54 + 126$$\Delta x = 180$[/tex]
Answer: n = 4 is more accurate than n = 2, because, if we use more subdivisions, it gives us a better estimate. In other words, as n increases, the accuracy of our estimate increases.
The lower estimate for the total distance traveled using n = 4 is: [tex]$\Delta x = \sum_{i=1}^4 v(t_i) \Delta t$[/tex]Here,
[tex]$\Delta t = \dfrac{12-0}{4}=3$[/tex].
Let us now use the lower estimate and substitute the minimum value of velocity in the formula.
[tex]$\Delta x = v(0)3 + v(3)3 + v(6)3 + v(9)3 + v(12)3$$\Delta x = 0(3) + 3(3) + 6(3) + 9(3) + 12(3)$$\Delta x = 0 + 9 + 18 + 27 + 36$$\Delta x = 90$[/tex].
To know more about velocity visit:
https://brainly.com/question/24259848
#SPJ11
For the graph Y at right: (a) Prove or disprowe that Y has an Euler circuit. B . D EC F G H K (b) Prove or disprove that Y has an Euler path. (By convention, Euler paths are non-closed.) (c) Prove or disprove that Y has a Hamilton circuit. (d) Prove or disprove that Y has a Hamilton path. (By convention. Hamilton paths are non-closed.)
Answers
a. The prove whether the graph Y at right has an Euler circuit or not.An Euler Circuit is defined as a circuit that traverses every edge of a graph once and only once and returns to its starting point.
To prove that a graph Y has a Euler circuit, it must satisfy the following conditions: Every vertex in the graph should have even degrees. If one vertex has odd degree, it won't be able to return to the starting point and complete the circuit. The graph must be connected and not have any vertices with 0 degree or isolated vertices. Using the graph provided, the vertices, their degrees, and the degrees are A: 3B: 4C: 2D: 4E: 3F: 3G: 3H: 2I: 1J: 2K: 2The degrees of the vertices in the graph above are all even, except vertex I, which is odd. Hence, it is impossible to construct an Euler circuit in the graph. Therefore, the main answer to part (a) is disproved. b.
The part (b) of the question is to prove whether Y has an Euler path or not. An Euler path is defined as a path that traverses every edge of a graph once and only once and does not have to return to its starting point. To prove that a graph Y has an Euler path, it must satisfy the following conditions:It must have exactly 2 vertices with odd degrees, and the other vertices must have even degrees. If a graph has more than 2 vertices with odd degrees, it cannot have an Euler path. If it has zero vertices with odd degrees, it can have an Euler path, but it will also have an Euler circuit since there are no vertices left out.
Using the graph provided, there are 2 vertices with odd degrees, namely A and E. The other vertices have even degrees, so the graph Y has an Euler path. Therefore, the main answer to part (b) is proved.c. The explanation for part (c) of the question is to prove whether Y has a Hamilton circuit or not.A Hamilton circuit is defined as a circuit that passes through each vertex of a graph once and only once. To prove that a graph Y has a Hamilton circuit, the following conditions must be satisfied:
The graph must be connected. All vertices in the graph must have a degree of at least 2.If a graph satisfies these conditions,
it may have a Hamilton circuit, but there is no guarantee. Using the graph provided, there is no Hamilton circuit that can pass through all the vertices in the graph Y only once. Therefore, the main answer to part (c) is disproved. d. The explanation for part (d) of the question is to prove whether Y has a Hamilton path or not .A Hamilton path is defined as a path that passes through each vertex of a graph once and only once. To prove that a graph Y has a Hamilton path, the following conditions must be satisfied: The graph must be connected. All vertices in the graph must have a degree of at least 1.If a graph satisfies these conditions, it may have a Hamilton path, but there is no guarantee. Using the graph provided, there is no Hamilton path that can pass through all the vertices in the graph Y only once.
Therefore, the main answer to part (d) is disproved. the main answer for part (a) is disproved, the main answer for part (b) is proved, the main answer for part (c) is disproved, and the main answer for part (d) is disproved.
To know more about degrees visit:
https://brainly.com/question/364572
#SPJ11
i need solving by using charnes and coopers
and using Simplex two phase
Max f(x) = 4X₁ + 3X₂ 3X₁ + 2X₂ +1 sit 3X₁ +5X2₂ < 15 5 X₁ + 2x₂ 5 10 By using charnes and cooper tj Xi X₁ = t₁ = t₂ D(X) Max Lt) 4 +₁ + 3 = ₂ sit 3+₁ +5+₂ -15 to < 0 5t�
Answers
Charnes and Cooper's method is a method for transforming a linear programming problem involving inequalities and equalities to an equivalent linear programming problem involving only equalities.
The given linear programming problem can be solved by using Charnes and Cooper method and using Simplex two-phase.
Max f(x) = 4X₁ + 3X₂ 3X₁ + 2X₂ +1
sit 3X₁ +5X2₂ < 15 5 X₁ + 2x₂ 5 10
By using charges and cooper tj XiX₁ = t₁ = t₂D(X)
Max Lt) 4 +₁ + 3 = ₂
sit 3+₁ +5+₂ -15 to < 0 5t ≤ 10. By substituting X₁ = t₁ = t₂, the problem can be converted into the following problem.
Maximize Z = Lt 4t1 + 3t2 − 0s1 − 0s2 − s3.
Subject to the following constraints:
3t1 + 5t2 + s3 = 15 (1)
5t1 + 2t2 + s4 = 5 (2)
t1 + t2 + s5 = 10 (3) where, Z is the objective function, s1, s2, s3, s4, and s5 are the slack variables of the system which are added to balance the equation, and t1 and t2 are the new variables replacing X1 and X2. Now, the. The simplex two-phase method can be used to solve the problem.
To know more about Linear Programming Problems visit:
https://brainly.com/question/29405477
#SPJ11
a) Give an intuitive reason why the connected sum operation does
not have an inverse.
b) Rigorously prove that the connected sum operation does not
have an inverse.
Answers
The connected sum operation does not have an inverse as it destroys information about the original spaces.
A simple intuitive reason for this is that if one connects two spaces, the operation doesn't have any way of determining which space is the "original" one, and which one is the "newly added" one.
The connected sum of two spaces X and Y is defined as follows: take a copy of X, a copy of Y, remove an open ball from each of them, and then glue the resulting two spaces together along the open balls' boundaries. This is denoted by $X \# Y$.The connected sum operation does not have an inverse, which can be rigorously proved as follows:
Similarly, $Z$ is orientable if and only if both $X$ and $Y$ are orientable.
Learn more about inverse click here:
https://brainly.com/question/3831584
#SPJ11
let l : r3 →r2 be a linear operator given by t (x) = ax. find the matrix a such that l 1 0 1 = (2 0 ) , l 1 1 0 = ( 4 −1 ) , l 0 2 −1 = ( 5 −1
Answers
The matrix a for linear operator given by t (x) = ax, such that l 1 0 1 = (2 0 ) , l 1 1 0 = ( 4 −1 ) , l 0 2 −1 = ( 5 −1 ) is given by the matrix a = 2 4 5 0 -1 -1.
The matrix a such that l 1 0 1 = (2 0 ) , l 1 1 0 = ( 4 −1 ) , l 0 2 −1 = ( 5 −1 ) is given by: a = (l(e1) l(e2) l(e3)) where e1, e2, e3 are the standard basis vectors in R3. Therefore, we need to find l(e1), l(e2), l(e3).Note that e1 = (1, 0, 0), e2 = (0, 1, 0), e3 = (0, 0, 1).
Also, we know that l(x) = ax, where a is the matrix of l with respect to the standard basis in R3 and the standard basis in R2. Now, l(e1) = (2, 0), l(e2) = (4, -1), l(e3) = (5, -1).
Therefore, a = [l(e1) l(e2) l(e3)] = 2 4 5 0 -1 -1.
To know more about linear operator, visit:
https://brainly.com/question/30891905
#SPJ11
The given operator is:
l : R3 → R2 given by t(x) = ax.
The matrix representation of the operator L is given by:
L = [t(e1) t(e2) t(e3)] = [ae1 ae2 ae3]
Where, {e1, e2, e3} is the standard basis for R3, and {t(e1), t(e2)} is the standard basis for R2.
Given,
L[1 0 1] = [2 0] ... (1)L[1 1 0] = [4 -1] ... (2)L[0 2 -1] = [5 -1] ... (3)
Using matrix multiplication in equation (1) and comparing coefficients with the right-hand side, we get:
[a 0 a] = [2 0]So, a = 2.
Using matrix multiplication in equation (2) and comparing coefficients with the right-hand side, we get:
[2a 2a 0] = [4 -1]
So, 4a = 4, and -a = -1.
Hence, a = 1.
Using matrix multiplication in equation (3) and comparing coefficients with the right-hand side, we get:
[0 2a -a] = [5 -1]So, 2a = 5, and a = 5/2.
Substituting the values of a, we have:
A = [2 0 2, 2 2 -1] = [2 0 2;2 2 -1].
Hence, the matrix representation of the operator L is A = [2 0 2;2 2 -1].
The answer is : A = [2 0 2;2 2 -1].
Given,L[1 0 1] = [2 0] ... (1)L[1 1 0] = [4 -1] ... (2)L[0 2 -1] = [5 -1] ... (3)
We need to find the matrix A such that, L = Ax.
Let the matrix A be of the form, A = [a1 a2 a3;b1 b2 b3]
Where, {a1 a2 a3} and {b1 b2 b3} are the columns of the matrix A.
Then, L = Ax can be written as [t(e1) t(e2) t(e3)] = [ae1 ae2 ae3;be1 be2 be3]
Simplifying, we getL = [t(e1) t(e2) t(e3)] = [a1b1 a2b2 a3b3] ... (1)
Now, using equation (1) we can write,L[1 0 1] = [2 0] as [a1b1 a2b2 a3b3] [1 0 1]T = [2 0] ... (2)L[1 1 0] = [4 -1] as [a1b1 a2b2 a3b3] [1 1 0]T = [4 -1] ... (3)L[0 2 -1] = [5 -1] as [a1b1 a2b2 a3b3] [0 2 -1]T = [5 -1] ... (4)
Here, T denotes the transpose of the matrix. Using matrix multiplication in equation (2) and comparing coefficients with the right-hand side, we get,
[a1 a2 a3] [1 0 1]T = [2 0] ... (5)
Similarly, using matrix multiplication in equation (3) and comparing coefficients with the right-hand side, we get,
[a1 a2 a3] [1 1 0]T = [4 -1] ... (6)
And using matrix multiplication in equation (4) and comparing coefficients with the right-hand side, we get,
[a1 a2 a3] [0 2 -1]T = [5 -1] ... (7)
Solving equations (5), (6), and (7), we can find the values of the matrix A.
To know more about matrix, visit:
https://brainly.com/question/29132693
#SPJ11
Why
the formula of a distance from a point to a line in 3D is different
from the formula of a point to a line in 3D?
pls explain in sentence
Answers
The formula for finding the distance from a point to a line in 3D is different from the formula for finding the distance between two points in 3D because they involve different geometric concepts.
When finding the distance from a point to a line in 3D, we are interested in measuring the shortest distance between a specific point and a line. This involves considering the perpendicular distance from the point to the line, and the formula takes into account this perpendicular distance along with the position of the point and the line in 3D space.
On the other hand, when finding the distance between two points in 3D, we are measuring the straight-line distance between the two points. This distance can be calculated using the formula derived from the Pythagorean theorem, which considers the differences in the coordinates of the two points in each dimension (x, y, and z) to calculate the overall distance.
In summary, the formulas for finding the distance from a point to a line and the distance between two points in 3D differ because they address different geometric relationships and measurements in 3D space.
To learn more about Pythagorean theorem, click here: brainly.com/question/14930619
#SPJ11
Find an equation of the line parallel to 3x-y=6 and passing through (3,7). Express the equation in standard form. Which of the following is the equation of a line parallel to 3x-y=6 and passing through (3,7)? O A. x+3y = 16 OB. 3x-y=16 OC. x+3y=2 OD. 3x-y=2
Answers
A linear equation is expressed in its standard form as Axe + By = C, where A, B, and C are all constants and A and B are not equal to zero.
The variables (x and y) are on the left side of the equation and the constant term is on the right side of the equation in this form, where the coefficients A, B, and C are normally integers.
To find an equation of a line parallel to 3x - y = 6, we need to determine the slope of the given line.
Rearranging the equation 3x - y = 6 into slope-intercept form (y = mx + b) by isolating y, we get:
y = 3x - 6
From this equation, we can see that the slope of the given line is 3.
Since parallel lines have the same slope, any line parallel to 3x - y = 6 will also have a slope of 3.
Now, using the point-slope form of a line, we can find the equation of the line passing through the point (3,7) with a slope of 3.
The point-slope form is given by:
y - y₁ = m(x - x₁),
where (x₁, y₁) is the given point and m is the slope.
Substituting the values, we get:
y - 7 = 3(x - 3)
Expanding and simplifying:
y - 7 = 3x - 9
Rearranging the equation into standard form (Ax + By = C), we get:
3x - y = 2
Comparing the equation 3x - y = 2 with the given options, we can see that the correct equation of a line parallel to 3x - y = 6 and passing through (3,7) is:
OD. 3x - y = 2
To know more about Standard Form visit:
https://brainly.com/question/12452575
#SPJ11
A pilot is flying an aircraft into a bad storm, at an airspeed of 450 km/h on a heading of S60°W. The ground velocity of the plane can be measured by 376 km/h at a bearing of $20°W. Determine the wind speed and its direction. You must include a labelled vector diagram. Round side lengths to 3 decimal places and angles to the nearest whole degree.
Answers
The wind speed is approximately 243.372 km/h, blowing in a direction of S81°W. This is determined by calculating the vector difference between the ground velocity and the airspeed.
To solve this problem, we need to calculate the vector difference between the ground velocity and the airspeed. Let's start by breaking down the given information. The airspeed is 450 km/h with a heading of S60°W, while the ground velocity is 376 km/h at a bearing of $20°W.
First, we convert the headings into compass bearings. S60°W is equivalent to S120°E, and $20°W is equivalent to N160°E. Now we can represent the airspeed and ground velocity as vectors on a diagram.
Next, we subtract the airspeed vector from the ground velocity vector to obtain the wind vector. Using vector subtraction, we find that the resultant vector has a magnitude of approximately 243.372 km/h.
Finally, we determine the direction of the wind vector by finding the bearing angle. The bearing angle is measured clockwise from the north, so we subtract 160° from 120° to get a bearing angle of 80°. However, since the wind is blowing in the opposite direction, we subtract 180° from 80° to obtain a direction of S81°W.
In conclusion, the wind speed is approximately 243.372 km/h, blowing in a direction of S81°W.
Learn more about vector here:
https://brainly.com/question/24256726
#SPJ11
Let Y₁, Y2,..., Yn be a random sample from a population with probability mass function of the form 0(1-0)-¹, if y=1,2,..., p(Y = y) = 0, O.W., where 0 <<[infinity]. Estimate using the method of moment [2.5 points] and using the method of maximum likelihood estimation.
Answers
The method of moments estimate for 0 is 0, and the maximum likelihood estimate is undefined due to the nature of the probability mass function. To estimate the parameter 0 using the method of moments, we equate the sample moment to the population moment.
The first population moment (mean) is given by E(Y) = Σ(y * p(Y = y)), where p(Y = y) is the probability mass function.
Since p(Y = y) = 0 for y ≠ 1, we only consider y = 1.
E(Y) = 1 * p(Y = 1) =[tex]1 * 0(1 - 0)^(-1)[/tex] = 0
Setting the sample moment (sample mean) equal to the population moment, we have:
0 = (1/n) * ΣYᵢ
Solving for 0, we get the estimate for the parameter using the method of moments.
To estimate the parameter 0 using the method of maximum likelihood estimation (MLE), we maximize the likelihood function L(0) = Π(p(Y = yᵢ)), where p(Y = y) is the probability mass function.
Since p(Y = y) = 0 for y ≠ 1, the likelihood function becomes
L(0) = [tex]p(Y = 1)^n.[/tex]
To maximize L(0), we take the logarithm of the likelihood function and differentiate with respect to 0:
ln(L(0)) = n * ln(p(Y = 1))
Differentiating with respect to 0 and setting it equal to 0, we solve for the MLE of 0.
However, since p(Y = y) = 0 for y ≠ 1, the likelihood function will be 0 for any non-zero value of 0. Therefore, the maximum likelihood estimate for 0 is undefined.
In summary, the method of moments estimate for 0 is 0, and the maximum likelihood estimate is undefined due to the nature of the probability mass function.
To know more about Maximum likelihood estimation visit-
brainly.com/question/32530115
#SPJ11
If the product of 12 and a number is decreased by 36, the result is 60.
Answers
Answer: The number is [tex]x=8[/tex]
Step-by-step explanation:
Since decreasing the product of 12 and a number x by 36 results in 60, it follows:
[tex]12x-36=60\\12x=60+36\\12x=96\\x=\frac{96}{12}=8[/tex]
So, the number is [tex]x=8[/tex]
An investor is prepared to buy short term promissory notes at a price that will provide him with a return on investment of 12% What amount would he pay on August 9 for a 120 day note dated July 1 for $4100 with interest at 10.25% pa?
Answers
Therefore, the investor would pay approximately $4234.08 on August 9 for the 120-day note dated July 1.
To calculate the amount the investor would pay for the promissory note, we need to determine the interest earned during the 120-day period and add it to the principal amount.
First, let's calculate the interest earned:
Principal amount (P) = $4100
Interest rate (r) = 10.25% per annum = 10.25/100 = 0.1025
Time (t) = 120 days/365
Interest (I) = P * r * t
= $4100 * 0.1025 * (120/365)
≈ $134.08
Next, we add the interest to the principal amount to determine the total amount paid by the investor:
Total amount = Principal + Interest
= $4100 + $134.08
≈ $4234.08
To know more about investor,
https://brainly.com/question/32166790
#SPJ11
Determine whether the following matrices form a basis for M22 ?. 13 0 0 1 BRI 3 -2 -9 -3 3
Answers
The given matrices do not form a basis for M22.
Is it possible to form a basis with the given matrices?In linear algebra, a basis for a vector space is a set of vectors that are linearly independent and span the entire space. In the case of the matrix space M22, a basis would consist of matrices that satisfy these conditions. To determine whether the given matrices form a basis, we need to check for linear independence and span.
Firstly, we examine linear independence. A set of matrices is linearly independent if none of the matrices can be expressed as a linear combination of the others. To determine this, we can form an augmented matrix with the given matrices and row reduce it. If the row-reduced form has any rows of all zeros, it indicates linear dependence.
In the given case, forming the augmented matrix and row reducing it, we find that the row-reduced form has a row of all zeros. This implies that at least one matrix in the set can be expressed as a linear combination of the others, indicating linear dependence. Hence, the given matrices are not linearly independent.
Since the matrices are not linearly independent, they cannot span the entire space of M22. Therefore, the given matrices do not form a basis for M22.
Learn more about Matrices
brainly.com/question/24810141
#SPJ11
Estimate y(1.5) using Euler's method with h = 0.5
y = 4x+2/y
y(0) = 1
2. Sketch the isocline for the equation from question 1 that includes the initial point (0, 1)
Answers
The isocline that includes the point (0, 1) is the curve passing through (0, √2) and (0, -√2), since the slope of the curve is y' = 0 at these points.
For the value of y(1.5) we use Euler's method with h = 0.5 and the given differential equation,
Determine the slope of the tangent line at the initial point (0, 1):
y'(x) = (d/dx)(4x + 2/y)
= 4 - 2/y²
y'(0) = 4 - 2/1² = 2
Use the slope and the step size to find the approximation of y(0.5):
y(0.5) ≈ y(0) + h y'(0)
= 1 + 0.5 x 2
= 2
Repeat the process to estimate y(1):
y'(0.5) = 4 - 2/2² = 3
y(1) ≈ y(0.5) + h
y'(0.5) = 2 + 0.5 3
= 3.5
Repeat the process to estimate y(1.5):
y'(1) = 4 - 2/3.5² ≈ 3.66
y(1.5) ≈ y(1) + h y'(1) ≈ 3.5 + 0.5 x 3.66 ≈ 5.33
Therefore, using Euler's method with h = 0.5, we estimate that,
y(1.5) ≈ 5.33.
To sketch the isocline for the given differential equation that includes the initial point (0, 1), we need to find the values of y that make,
y' = 0: 4 - 2/y² = 0
y² = 2
y = ±√2
Thus, The isocline that includes the point (0, 1) is the curve passing through (0, √2) and (0, -√2), since the slope of the curve is y' = 0 at these points. And, the isoclines for this equation are hyperbolas centered at (0,0).
Learn more about the coordinate visit:
https://brainly.com/question/24394007
#SPJ4
Determine all solutions of the given equation. Express your answer(s) using radian measure. (Select all that apply.) 2 tan² x + sec² x - 2 = 0 a. x = π/3 + πk, where k is any integer b. x = π/6 + πk, where k is any integer c. x = 2π/3 + πk, where k is any integer d. x = 5π/6 + πk, where k is any integer
e. none of these
Answers
To solve the given equation 2tan²x + sec²x - 2 = 0, we can use trigonometric identities to simplify it and find the solutions.
Let's manipulate the equation step by step:
2tan²x + sec²x - 2 = 0
Using the identity sec²x = 1 + tan²x:
2tan²x + (1 + tan²x) - 2 = 0
Simplifying further:
3tan²x - 1 = 0
Now, let's solve this equation for tan²x:
3tan²x = 1
tan²x = [tex]\frac{1}{3}[/tex]
Taking the square root of both sides:
tanx = [tex]\pm\sqrt{\frac{1}{3}}[/tex]
The solutions for tanx are:
tanx = [tex]\sqrt{\frac{1}{3}}[/tex] and [tex]-\sqrt{\frac{1}{3}}[/tex]
To find the solutions for x, we'll determine the corresponding angles using the inverse tangent function:
[tex]x = \arctan\left(\sqrt{\frac{1}{3}}\right)[/tex]
[tex]x = \arctan\left(-\sqrt{\frac{1}{3}}\right)[/tex]
Using a calculator, we can find the values of x in the range [0, 2π):
x ≈ 0.61548 rad and x ≈ 2.52674 rad
Now, let's check the options provided:
a. [tex]x = \frac{\pi}{3} + \pi k[/tex], where k is any integer
Substituting k = 0, we have x = π/3, which is not one of the solutions we found.
b. [tex]x = \frac{\pi}{6} + \pi k[/tex], where k is any integer
Substituting k = 0, we have x = π/6, which is one of the solutions we found.
c. [tex]x = \frac{2\pi}{3} + \pi k[/tex], where k is any integer
Substituting k = 0, we have x = 2π/3, which is not one of the solutions we found.
d. [tex]x = \frac{5\pi}{3} + \pi k[/tex], where k is any integer
Substituting k = 0, we have x = 5π/6, which is one of the solutions we found.
Based on our analysis, the correct solutions are:
b. [tex]x = \frac{\pi}{6} + \pi k[/tex], where k is any integer
d. [tex]x = \frac{5\pi}{3} + \pi k[/tex], where k is any integer
Therefore, the answer is (b) and (d).
To know more about trigonometric identities visit:
https://brainly.com/question/24377281
#SPJ11
(a) If an initial deposit of 4000 euros is invested now and earns interest at an annual rate of 3%, mhow much will it have grown after 4 years if interest is compounded: (ii) quarterly? (i) yearly; (b) How long does it take for the 4,000 euros to triple with quarterly compounding of interest?
Answers
(a) If an initial deposit of 4000 euros is invested now and earns interest at an annual rate of 3%, then it has grown after 4 years if interest is compounded:
(i) yearly: A = 4641.60 euros
(ii) quarterly: A = 4644.38 euros
(b) It takes 27.17 years for the 4,000 euros to triple with quarterly compounding of interest.
(a) The initial deposit is 4000 euros
The interest rate is 3% per annum
Time for which it is compounded is 4 years
(i) Yearly calculation- The formula to calculate the compound interest annually is given by
A=P(1+r/n)^nt
Where A is the amount, P is the principal, r is the rate of interest, n is the number of times interest is compounded per year, and t is the time in years.
Substituting the values, we get
A = 4000(1 + 0.03/1)^(1*4)
A = 4000(1.03)^4
A = 4641.60 euros
The amount will be 4641.60 euros
(ii) Quarterly calculation- The formula to calculate the compound interest quarterly is given by
A=P(1+r/n)^nt
Where A is the amount, P is the principal, r is the rate of interest, n is the number of times interest is compounded per year, and t is the time in years.
Substituting the values, we get
A = 4000(1 + 0.03/4)^(4*4)
A = 4644.38 euros
The amount will be 4644.38 euros
(b) To find out how long it takes for the 4000 euros to triple, we need to calculate the time it takes for the amount to become three times its original value.
The formula to calculate the compound interest is given by
A = P(1 + r/n)^(nt)
Where A is the amount, P is the principal, r is the rate of interest, n is the number of times interest is compounded per year, and t is the time in years.
Substituting the values, we get
12,000 = 4000(1 + r/4)^(4t)3 = (1 + r/4)^(4t)
Taking the natural log of both sides, we get
ln(3) = 4t ln(1 + r/4)
Dividing by 4 ln(1 + r/4), we get
t = ln(3) / (4 ln(1 + r/4))
Substituting the value of r, we get
t = ln(3) / (4 ln(1 + 0.03/4))
t = 27.17 years
Therefore, it takes approximately 27.17 years for 4000 euros to triple when compounded quarterly.
To learn more about compound interest: https://brainly.com/question/28020457
#SPJ11
Find the value of log_6 7 • log_7 8 • .... • log_n (n+1) • log_(n+1) 6 = _____
Answers
The value of the expression `log_6 7 • log_7 8 • .... • log_n (n+1) • log_(n+1) 6` is `1`.
To find the value of the expression `log_6 7 • log_7 8 • .... • log_n (n+1) • log_(n+1) 6`,
you need to use the logarithmic identity which states that `loga (b) × logb (c) = loga (c)` provided that `
a`, `b`, and `c` are positive numbers and `b ≠ 1`.
Thus, applying this identity to the expression `log_6 7 • log_7 8 • .... • log_n (n+1) • log_(n+1) 6`,
we get:
`log_6 7 × log_7 8 × .... × log_n (n+1) × log_(n+1) 6= log_6 8 × log_8 9 × .... × log_n (n+2) × log_(n+2) 6= log_6 6= 1
To know more about expression visit;-
https://brainly.com/question/28170201
#SPJ11
23. DETAILS LARPCALC10CR 1.4.074. Find the difference quotient and simplify your answer. f(x) = 3x - x², f(3+h)-f(3), h+0 h
Answers
The difference quotient for the given function is (-h² - 6h) / h.
What is the simplified form of the difference quotient for f(x) = 3x - x²?The difference quotient is a mathematical expression used to approximate the derivative of a function. In this case, we are given the function f(x) = 3x - x², and we need to find the difference quotient f(3+h) - f(3) divided by h, as h approaches 0.
To simplify the difference quotient, we substitute the values into the given function. First, we evaluate f(3+h) by plugging in 3+h for x: f(3+h) = 3(3+h) - (3+h)². Expanding and simplifying, we get 9+3h + 3 - h² - 6h - h².
Next, we evaluate f(3) by plugging in 3 for x: f(3) = 3(3) - 3² = 9 - 9 = 0.
Now, we substitute the values back into the difference quotient: [9+3h + 3 - h² - 6h - h² - 0] / h.
Simplifying further, we combine like terms in the numerator: 12 + 3h - 2h² - 6h. Then, we divide the entire expression by h, canceling out the h terms that are common in the numerator and denominator.
The simplified form of the difference quotient is (-h² - 6h) / h.
Learn more about difference quotient
brainly.com/question/6200731
#SPJ11
the number of home runs hit per game for the millard girls' softball team are: 1, 2, 4, 3, 2, 4, 3, 0, 1, 2, 3, 5, 2, 1, and 5.
Answers
The number of games played is not given in the question, so the answer cannot be determined.
The term "average" typically refers to the central tendency of a set of values or data points. It is a measure that represents the typical or typical value within a dataset. There are different types of averages commonly used, including the mean, median, and mode.
The given number of home runs hit per game for the Millard girls' softball team are: 1, 2, 4, 3, 2, 4, 3, 0, 1, 2, 3, 5, 2, 1, and 5.
According to the given data, the total number of home runs hit by the Millard girls' softball team would be:
1 + 2 + 4 + 3 + 2 + 4 + 3 + 0 + 1 + 2 + 3 + 5 + 2 + 1 + 5 = 38.
The average number of home runs hit by the Millard girls' softball team in each game can be calculated by dividing the total number of home runs by the number of games played.
The number of games played is not given in the question, so the answer cannot be determined.
To know more about average , visit
https://brainly.com/question/24057012
#SPJ11
find the torque τ about p due to f⃗ . your answer should correctly express both the magnitude and sign of τ . express your answer in terms of rm and f or in terms of r , θ , and f .
Answers
Torque is the cross product of the distance from the pivot point to the force, denoted by r, and the force applied, denoted by F. τ= r×F, where r is the moment arm, and F is the force. The direction of torque is either clockwise or counterclockwise depending on whether the force causes rotation that is clockwise.
Also, it is denoted by a positive sign for a counterclockwise torque and a negative sign for a clockwise torque.Let's assume that the vector F, acting on a rigid body about pivot point P, creates a moment, i.e., torque. The torque about P is determined by the product of the force magnitude, F, and the perpendicular distance, rm, from point P to the line of action of F.
That is, τ=rm ×F. If F and rm are known, we may substitute them into the equation to obtain the torque in the direction of rotation.τ = rm × Fsin(θ) where θ is the angle between the two vectors F and rm.Therefore, the torque about P due to F is expressed in terms of rm and F or in terms of r, θ, and F as τ=rm ×Fsin(θ) or τ = rFsin(θ), respectively.
To know more about product visit:
https://brainly.com/question/31815585
#SPJ11
Sketch the region enclosed by the given curves. Decide whether to integrate with respect to x or y. Then find the area of the region. ㅠ ㅠ y = 9 cos(x), y = (6 sec(x))², x = x = 4' 4 Question Help
Answers
The region enclosed by the curves y = 9cos(x), y = (6sec(x))², and x = 4' 4 needs to be sketched and the area of the region needs to be found.
To sketch the region enclosed by the given curves, we first need to find the points of intersection between the curves. Setting the two equations for y equal to each other, we have:9cos(x) = (6sec(x))²
Simplifying this equation, we get:9cos(x) = 36sec²(x)
Dividing both sides by 36 and taking the square root, we have:
cos(x) = √(1/4)
cos(x) = ±1/2
This means that x can be either π/3 or 5π/3. Plugging these values back into the equations for y, we find the corresponding y-values:
y = 9cos(π/3) = 9(1/2) = 9/2
y = 9cos(5π/3) = 9(-1/2) = -9/2
Now we can sketch the region on the xy-plane. The region is bounded by the curves y = 9cos(x), y = (6sec(x))², and the vertical line x = 4' 4 (which indicates that the region extends infinitely in the positive x-direction). The region is symmetric about the x-axis due to the cosine function, and it is also bounded below by the x-axis. To find the area of this region, we need to integrate with respect to x. However, since the region is symmetric about the x-axis, we can calculate the area of the upper half and double it.
Therefore, the area of the region is:
2 ∫[π/3, 4' 4] 9cos(x) dx = 2 [9sin(x)] [π/3, 4' 4] = 18(sin(4' 4) - sin(π/3))
To learn more about curves click here
brainly.com/question/31114246
#SPJ11
what is return on assets for 2022? (round answer to 1 decimal place, e.g. 15.2.)
Answers
The return on assets for 2022 can be calculated by dividing the net income by the average total assets for that year.
Return on Assets (ROA) is calculated by dividing a company's net income by its average total assets. The formula for ROA is as follows:
ROA = (Net Income / Average Total Assets) * 100
Once we have the net income and average total assets for 2022, we can plug them into the ROA formula to calculate the return on assets. The result will be expressed as a percentage, which indicates how effectively the company is utilizing its assets to generate profits.
The return on assets provides insights into the company's ability to generate profits relative to the size of its asset base. It is particularly useful when comparing companies within the same industry or when analyzing a company's performance over time.
A high return on assets suggests that the company is utilizing its assets efficiently to generate profits, while a low return on assets may indicate inefficiencies or underutilization of assets.
By analyzing the return on assets, investors and analysts can gain a better understanding of a company's financial performance and make informed decisions about investing in or lending to the company.
It helps to assess the company's ability to generate profits from its assets and provides a basis for comparing its performance to its peers.
To know more about assets here
https://brainly.com/question/14826727
#SPJ4
(a) In an investigation of toxins produced by molds that infect corn crops, a biochemist prepares extracts of the mold culture with organic solvents and then measures the amount of the toxic substance per gram of solution. From 10 preparations of the mold culture, the following measurements of the toxic substance (in milligrams) are obtained:
1.2, 1.5, 1.6, 1.6, 2.0, 2.0, 1.8, 1.8, 2.2, 2.2
Find a 99% confidence interval for the mean weight (in milligrams) of toxic substance per gram of mold culture in the sampled population.
(b) Which of the following statements is true regarding part (a)?
Problem #7(a):
confidence interval
enter your answer in the form a,b
(numbers correct to 2 decimals)
(A) The population does not need to be normal. (B) The population mean must be inside the confidence interval.
(C) The population must be normal. (D) The population must follow a t-distribution.
(E) The population standard deviation o must be known.
Problem #7(b):
C
Just Save
Your work has been saved! (Back to Admin Page).
Submit Problem #7 for Grading
Problem #7 Attempt #1 Attempt #2 Attempt #3
Your Answer: 7(a) 7(a) 7(a)
7(b) 7(b) 7(b)
Your Mark: 7(a) 7(a) 7(a)
7(b) 7(b) 7(b)
Answers
(a) The 99% confidence interval for the mean weight of the toxic substance per gram of mold culture is approximately 1.612 to 2.108 milligrams. (b) The correct statement is (A) The population does not need to be normal.
(a) To find the 99% confidence interval for the mean weight of the toxic substance per gram of mold culture, we can use the following steps:
1, Calculate the sample mean (x) of the measurements provided. Add up all the values and divide by the total number of measurements (in this case, 10).
x = (1.2 + 1.5 + 1.6 + 1.6 + 2.0 + 2.0 + 1.8 + 1.8 + 2.2 + 2.2) / 10 ≈ 1.86
2, Calculate the sample standard deviation (s) of the measurements. This measures the variability in the data.
s = √[((1.2 - 1.86)² + (1.5 - 1.86)² + ... + (2.2 - 1.86)²) / (10 - 1)] ≈ 0.302
3, Determine the critical value (z*) corresponding to the desired confidence level of 99%. This value can be obtained from the standard normal distribution table or using statistical software. For a 99% confidence level, the critical value is approximately 2.62.
4, Calculate the margin of error (E) using the formula:
E = z* * (s / √n)
where z* is the critical value, s is the sample standard deviation, and n is the sample size.
E = 2.62 * (0.302 / √10) ≈ 0.248
5, Finally, construct the confidence interval by subtracting and adding the margin of error to the sample mean:
Confidence interval = x ± E = 1.86 ± 0.248
Therefore, the 99% confidence interval for the mean weight of the toxic substance per gram of mold culture is approximately 1.612 to 2.108 milligrams.
(b) The correct statement regarding part (a) is (A) The population does not need to be normal.
The confidence interval for the mean can be calculated without assuming that the population follows a specific distribution, as long as the sample size is large enough (n ≥ 30) or the population is approximately normally distributed.
To know more about confidence interval:
https://brainly.com/question/31482147
#SPJ4
Let G be a simple graph with the vertex set V = {V1, V2, V3, V4, V5, V6}. Which of the following statements is certainly true about G? —
Select one or more:
a. G has at most 15 edges.
b. G has at least 5 edges.
c. If G is bipartite, then it has at least 5 edges.
d. If G contains a vertex of degree 5, then G has no isolated vertex.
e. If G is a complete graph, then it has 30 edges.
f. If G is bipartite, then it has at most 8 edges.
g. G contains a cycle.
Answers
The statement that is certainly true about the graph G is d. If G contains a vertex of degree 5, then G has no isolated vertex. Statement d is the only one that can be confirmed as true for the given graph G.
a. G has at most 15 edges: This statement cannot be determined based on the information provided. The number of edges in the graph G depends on the specific connections between the vertices, which are not given.
b. G has at least 5 edges: Similar to statement a, the number of edges cannot be determined without specific information about the connections in the graph.
c. If G is bipartite, then it has at least 5 edges: The statement cannot be confirmed as true since we don't know if G is bipartite or not. It is possible for a bipartite graph to have fewer than 5 edges.
d. If G contains a vertex of degree 5, then G has no isolated vertex: This statement is certainly true. If a vertex in G has a degree of 5, it means that it is connected to 5 other vertices. In order for the vertex to have no isolated vertices, it must be connected to all other vertices in the graph.
e. If G is a complete graph, then it has 30 edges: This statement cannot be confirmed as true since the number of vertices in graph G is not specified. The number of edges in a complete graph is determined by the number of vertices according to the formula (n * (n-1)) / 2, where n is the number of vertices.
f. If G is bipartite, then it has at most 8 edges: The statement cannot be confirmed as true since we don't know if G is bipartite or not. Bipartite graphs can have any number of edges depending on their specific connections.
g. G contains a cycle: The presence of a cycle in graph G cannot be determined based on the given information. It depends on the specific connections between the vertices, which are not provided.
Learn more about graph here: https://brainly.com/question/30934484
#SPJ11
Make up two vectors nonzero vectors v1 = (x1, yı) and v2 = (x2, y2) in R2 that are in different directions (i.e. one is not a scalar multiple of the other, or equivalently xi/yi and X2/y2 are different). Show how to 1. use the dot product to calculate the angle between these two vectors. 2. use the determinant to calculate the area of the parallelogram spanned by V1, V2 3. use geogebra (or python) to plot the parallelogram in the previous part, and see if your answer for the angle looks reasonable
Answers
The two vectors, V1 and V2 are defined as V1 = (x1, y1) and V2 = (x2, y2). Both of them are nonzero vectors and are in different directions. To answer the questions:
To use the dot product to calculate the angle between the two vectors:The formula to calculate the dot product is as follows, V1 . V2 = x1*x2 + y1*y2Using the above formula, the dot product of the two vectors is calculated as follows;V1 . V2 = (x1 * x2) + (y1 * y2)
So, the angle between the vectors can be calculated by taking the inverse cosine of the following formula:Cos θ = V1.V2/ (|V1|.|V2|)where V1.V2 is the dot product of V1 and V2, and |V1| and |V2| are the magnitudes of the two vectors.
The angle between the two vectors is shown below:
To calculate the area of the parallelogram spanned by V1, V2:The formula to calculate the area of a parallelogram spanned by two vectors is as follows:
Area of Parallelogram = |(V1 x V2)|where V1 x V2 is the cross product of V1 and V2, and |(V1 x V2)| is the magnitude of V1 x V2.So, the area of the parallelogram spanned by V1 and V2 is shown below:
To plot the parallelogram in the previous part, and see if your answer for the angle looks reasonable:
In order to plot the parallelogram using Python or Geogebra, we first need to create the vectors.
To know more about vector visit :-
https://brainly.com/question/24256726
#SPJ11
Write the equation of the ellipse that has a center at (-3,6), a
focus at (0,6), and a vertex at (2,6).
Answers
To write the equation of an ellipse, we need to determine its major and minor axes' lengths and the coordinates of its center.
Given:
Center: (-3, 6)
Focus: (0, 6)
Vertex: (2, 6)
The center is (-3, 6), which means the x-coordinate of the center is h = -3, and the y-coordinate is k = 6.
The distance between the center and a vertex is the semi-major axis (a). In this case, the distance between (-3, 6) and (2, 6) is 5 units, so a = 5.
The distance between the center and a focus is c. Since the focus is at (0, 6), the distance between (-3, 6) and (0, 6) is 3 units, so c = 3.
To find the semi-minor axis (b), we can use the relationship between a, b, and c in an ellipse:
c^2 = a^2 - b^2
Substituting the values we have:
3^2 = 5^2 - b^2
9 = 25 - b^2
b^2 = 25 - 9
b^2 = 16
b = 4
Now that we have the values for a, b, h, and k, we can write the equation of the ellipse:
(x - h)^2 / a^2 + (y - k)^2 / b^2 = 1
Substituting the values:
(x - (-3))^2 / 5^2 + (y - 6)^2 / 4^2 = 1
Simplifying:
(x + 3)^2 / 25 + (y - 6)^2 / 16 = 1
Therefore, the equation of the ellipse is:
(x + 3)^2 / 25 + (y - 6)^2 / 16 = 1
learn more about coordinates here: brainly.com/question/22261383
#SPJ11
Question 11 7 AGROPT DAY VIA MASTERY TEST TESTOPIES 1 TIOMETRIC RELATIONSHIPS & TRGONOMETRIC CONATIONS E Determine the radian measure of the complement of an angle that measures radians 11 radian
Answers
The radian measure of the complement of an angle that measures radians 11 radian is approximately -9.4292 rad.
What is a complement of an angle?
In mathematics, the complement of an angle refers to the angle that, when added to the given angle, results in a sum of 90 degrees or [tex]\frac{\pi }{2}[/tex] radians(a right angle).
To find the complement of an angle that measures 11 radians, we need to subtract the angle's measure from [tex]\frac{\pi }{2}[/tex] radians (which is equal to 90 degrees). The complement of an angle is the angle that, when combined with the given angle, forms a right angle.
Given:
Angle measure = 11 radians
Complement of the angle = [tex]\frac{\pi }{2}[/tex] - 11
Calculating the complement:
Complement = [tex]\frac{\pi }{2}[/tex] - 11
Using approximate values, [tex]\frac{\pi }{2}[/tex] ≈ 1.5708
Complement ≈ 1.5708 - 11
Complement ≈ -9.4292 radians
Therefore, the radian measure of the complement of an angle that measures 11 radians is approximately -9.4292 radians.
To learn more about complement of an angle from the given link
brainly.com/question/12555020
#SPJ4
A magazine reported that at the top 50 business schools in a? region, students studied an average of 14.8 hours. Set up a hypothesis test to try to prove that the mean number of hours studied at your school is different from the reported 14.8 hour benchmark. Complete parts? (a) through? (c) below.
a. State the null and alternative hypotheses. Choose the correct answer below.
b. What is a Type I error for your? test?
A. Concluding that the mean number of hours studied at your school is different from the reported 14.8 hour benchmark when in fact it is not different
B.Concluding that the mean number of hours studied at your school is different from the reported 14.8 hour benchmark when in fact it is different
C.Concluding that the mean number of hours studied at your school is not different from the reported 14.8 hour benchmark when in fact it is different
c. What is a Type II error for your? test?
A.Concluding that the mean number of hours studied at your school is not different from the reported14.8 hour benchmark when in fact it is different
B.Concluding that the mean number of hours studied at your school is different from the reported 14.8 hour benchmark when in fact it is not different
C.Concluding that the mean number of hours studied at your school is not different from the reported 14.8 hour benchmark when in fact it is not different
Answers
A hypothesis test is conducted to determine if the mean number of hours studied at a school is different from a benchmark.
a. Null hypothesis: The mean number of hours studied at your school is not different from the reported 14.8 hour benchmark.
Alternative hypothesis: The mean number of hours studied at your school is different from the reported 14.8 hour benchmark.
b. A Type I error for this test is A. Concluding that the mean number of hours studied at your school is different from the reported 14.8 hour benchmark when in fact it is not different. This means rejecting the null hypothesis when it is actually true.
c. A Type II error for this test is B. Concluding that the mean number of hours studied at your school is not different from the reported 14.8 hour benchmark when in fact it is different. This means failing to reject the null hypothesis when it is actually false.
Learn more about Null hypothesis here:
brainly.com/question/32456224
#SPJ11
Roger Bennett qualified and got a licence to sell real estate and then accepted a sales position with Max Reality- a leading real estate agency. To prepare for this position, he purchased and read a research report entitled "Buying Habits of Today's Home Buyer". Mr Bennett is attempting to develop a p
a. roduct strategy.
b. relationship strategy.
c. presentation strategy.
d. customer strategy.
e. promotion strategy.
Answers
Based on the given information, Mr. Bennett's purchase and reading of the research report on "Buying Habits of Today's Home Buyer" indicates his focus on developing a product strategy to align his offerings with the preferences and needs of potential customers in the real estate market. Thus, the correct option is :
(a) product strategy.
Analyzing each of the given options :
a. Product Strategy:
By purchasing and reading the research report on the "Buying Habits of Today's Home Buyer," Mr. Bennett is seeking valuable insights into the preferences and behaviors of potential customers in the real estate market. This information is crucial for developing a product strategy. A product strategy involves identifying and defining the features, benefits, and positioning of the products or services being offered. It helps in determining what types of properties, amenities, or services to focus on based on customer preferences and needs. By leveraging the information from the research report, Mr. Bennett can align his offerings with the demands of today's home buyers, potentially giving him a competitive advantage in the market.
b. Relationship Strategy:
A relationship strategy is focused on building and maintaining strong relationships with customers. While it is important for Mr. Bennett to establish relationships with potential buyers and clients as a real estate agent, the given information does not explicitly indicate that he is specifically developing a relationship strategy. The emphasis is more on acquiring knowledge about buyer habits rather than building relationships.
c. Presentation Strategy:
A presentation strategy typically refers to the techniques and approaches used to effectively communicate and present products or services to customers. While this is an important aspect of the real estate sales process, the given information does not suggest that Mr. Bennett is specifically focusing on developing a presentation strategy. The focus is more on gaining insights from the research report rather than on how to present or communicate the products or services.
d. Customer Strategy:
A customer strategy involves understanding and segmenting the target customer base, identifying their needs and preferences, and developing approaches to attract and retain customers. While understanding the buying habits of today's home buyers is important for developing a customer strategy, the given information does not provide sufficient details to conclude that Mr. Bennett is specifically developing a customer strategy.
e. Promotion Strategy:
A promotion strategy typically involves planning and implementing various marketing and advertising activities to create awareness and generate interest in products or services. While promoting real estate properties is a crucial aspect of the sales process, the given information does not explicitly indicate that Mr. Bennett is specifically focusing on developing a promotion strategy. The emphasis is more on gaining knowledge from the research report rather than on promotional activities.
In summary, based on the given information, Mr. Bennett's action of purchasing and reading the research report suggests that he is attempting to develop a product strategy. By understanding the buying habits of today's home buyers, he can align his offerings to meet their needs and preferences, giving him a competitive edge in the real estate market. Therefore, the correct option is (a).
To learn more about product strategy visit : https://brainly.com/question/30331359
#SPJ11
Let X and Y are two independent random variables with U(0, 1)
distributions. The two random
variables U and V are defined as U = X − Y and V = Y .
a. Find the joint distribution of U and V .
Answers
The joint distribution of U and V is constant and equal to 1.
To find the joint distribution of U and V, given that X and Y are independent random variables with U(0, 1) distributions, we can express U = X - Y and V = Y.
Since X and Y have uniform distributions, their joint PDF is 1. Applying the probability transformation formula and calculating the Jacobian matrix, we find that the determinant of the Jacobian is 1. Therefore, the joint distribution of U and V is given by fU, V(u, v) = 1.
This implies that U and V are independent random variables, and their joint distribution is constant and equal to 1 over the range of U and V. In other words, the probability of any specific combination of U and V is the same, regardless of their values.
To learn more about “distribution” refer to the https://brainly.com/question/27905732
#SPJ11
find the directional derivative of f(x,y,z)=xy z^2, at (3,2,1) in the direction of v⃗ =i⃗ j⃗ k
Answers
The directional derivative of a function f(x, y, z) at a point (a, b, c) in the direction of a vector v⃗ = <v₁, v₂, v₃> is given by the dot product of the gradient of f and the unit vector in the direction of v⃗.
First, let's find the gradient of f(x, y, z):
∇f(x, y, z) = <∂f/∂x, ∂f/∂y, ∂f/∂z>
For f(x, y, z) = xy z², we have:
∂f/∂x = yz²
∂f/∂y = xz²
∂f/∂z = 2xyz
So, the gradient of f(x, y, z) is:
∇f(x, y, z) = <yz², xz², 2xyz>
Now, let's find the unit vector in the direction of v⃗ = <v₁, v₂, v₃>:
|v⃗| = √(v₁² + v₂² + v₃²)
|v⃗| = √(1² + 1² + 1²)
|v⃗| = √3
The unit vector in the direction of v⃗ is:
u⃗ = v⃗ / |v⃗|
u⃗ = <1/√3, 1/√3, 1/√3>
Finally, the directional derivative of f(x, y, z) at (3, 2, 1) in the direction of v⃗ = <i⃗, j⃗, k⃗> is given by:
Dv(f) = ∇f(a, b, c) · u⃗
Dv(f) = ∇f(3, 2, 1) · <1/√3, 1/√3, 1/√3>
Dv(f) = <(yz²)(3) + (xz²)(2) + (2xyz)(1)> · <1/√3, 1/√3, 1/√3>
Dv(f) = <3yz² + 2xz² + 2xyz> · <1/√3, 1/√3, 1/√3>
Therefore, the directional derivative of f(x, y, z) at (3, 2, 1) in the direction of v⃗ = <i⃗, j⃗, k⃗> is 3yz² + 2xz² + 2xyz.
To know more about directional derivative, refer here:
https://brainly.com/question/29451547#
#SPJ11