Answers
Answer:
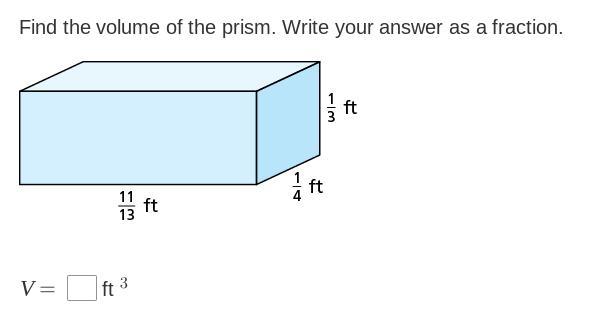
[tex] \frac{11}{13} \times \frac{1}{4} \times \frac{1}{3} = \frac{11}{156} [/tex]
So the volume of this rectangular prism is 11/156 of a cubic foot.
Related Questions
If anyone is reading this, rn i would be so flipping happy if u got this for me ive been waiting for so long and got nothing please answer correctly please
Answers
Answer: The answer is A.
Step-by-step explanation: Because I am smart don't underestimate me.
Answer:
C
Step-by-step explanation: (look at attachment)
3x + 4 = -2x -2
By looking at the y-intercepts, you automatically know the answer is C.
The y-intercept of the pink line is 4 because of 3x + 4.
The y-intercept of the blue line is -2, because of -2x - 2.
Charlie made the following table to record the height of each person in his family.
If Cheyenne and Hannah lay end to end, how far will they reach?
A. 9
B. 9, 1/2
C. 10
D. 8
Answers
Please help me so i can finish my homework
Answers
Answer:
[tex]\frac{1}{4}[/tex]w + 3
Step-by-step explanation:
Helping in the name of Jesus.
A rock of radioactive material has 500 atoms in it. The number of atoms decreases at a rate of 11% a day. Write an exponential function that models this situation. f(x) type your answer... (1 choose your answer... choose your answer... ✓)^x
Answers
Answer:
[tex]f(x) = 500( {.89}^{x} )[/tex]
The lengths of two sides of a triangle are 5.2 inches and 3.1 inches. Which lengths, in inches, could be the length of the third side?
Answers
The length of the third side between 2.1 inches and 8.3 inches (exclusive) could be a valid length for the third side of the triangle.
Triangle Inequality Theorem:In a triangle, the length of any side must be less than the sum of the lengths of the other two sides and greater than the difference between the lengths of the other two sides.
We can apply this rule to find the possible lengths of the third side of the triangle, given that the lengths of the two sides are 5.2 inches and 3.1 inches.
Here we have
The lengths of two sides of a triangle are 5.2 inches and 3.1 inches
Let's denote the length of the third side as x. Then, we have:
3.1 + 5.2 > x > 5.2 - 3.1
8.3 > x > 2.1
Therefore, the length of the third side x must be greater than 2.1 inches and less than 8.3 inches.
We can write this as an inequality:
2.1 < x < 8.3
Therefore,
The length of the third side between 2.1 inches and 8.3 inches (exclusive) could be a valid length for the third side of the triangle.
Learn more about Triangles at
https://brainly.com/question/12943336
#SPJ1
Number 7. I don’t understand, what’s the fraction? How do you get fraction and the + a number.
Answers
Answer:
A
Step-by-step explanation:
Equation of a line is: y = mx + b where m = slope b = y axis intercept
To find the slope between any two of the given points :
say 18, 100 and 27, 85
m = slope = (y1-y2) / (x1-x2) = (85-100) / ( 27-18) = -15/12 = -5/3
so now you have
y = - 5/3 x + b we still need to find the value of b
use any point to calculate b
say 15, 106
106 = - 5/3 (15) + b
b = ~ 131
the equation is then y = - 5/3 x + 131 closest to answer 'A'
Find the measures of angle a and B. Round to the
nearest degree.
Answers
The measure of angle A and B is 29° and 61° respectively
What is trigonometric ratio?Trigonometric Ratios are defined as the values of all the trigonometric functions based on the value of the ratio of sides in a right-angled triangle.
sin(tetha) = opp/hyp
tan(tetha) = opp/adj
cos(tetha) = adj/hyp
The opposite is 6 and the adjascent = 11
Therefore tan (tetha) = 11/6 = 1.833
tetha = tan^-1( 1.833)
= 61°( nearest degree)
The sum of angle in a triangle is 180°
therefore,
angle A = 180-( 61+90)
= 180-151
= 29°
therefore the measure of angle A and B is 29° and 61° respectively.
learn more about trigonometric ratio from
https://brainly.com/question/24349828
#SPJ1
justin developed the below hypothesis. h1: younger adults (18-28 years old) spend more time on social media than the middle-aged (29-65 years old) group and older adults (older than 65 years old). what statistical test should he use to test his hypothesis?
Answers
To verify if older adults and middles ages people spend less time on social media, Justin can use the Analysis of variance (ANOVA) test.
ANOVA is used to compare means across two or more groups. Justin can use this test on the different category of younger adults, middle-aged and older adult. This test is done when there is statistically significant difference between the group of samples.
Justin can utilize post-hoc tests (such as Tukey's HSD and Bonferroni) to identify whether particular groups are statistically different from one another if an ANOVA shows a significant difference.
To know more about ANOVA test, visit,
https://brainly.com/question/30127764
#SPJ4
Question 5
A recent conference had 900 people in attendance. In one exhibit room of 80 people, there were 65 teachers and 15 principals. What prediction can you make about the number of principals in attendance at the conference?
There were about 820 principals in attendance.
There were about 731 principals in attendance.
There were about 208 principals in attendance.
There were about 169 principals in attendance.
Question 6
A teacher was interested in the subject that students preferred in a particular school. He gathered data from a random sample of 100 students in the school and wanted to create an appropriate graphical representation for the data.
Which graphical representation would be best for his data?
Stem-and-leaf plot
Histogram
Circle graph
Box plot
Question 7
A random sample of 100 middle schoolers were asked about their favorite sport. The following data was collected from the students.
Sport Basketball Baseball Soccer Tennis
Number of Students 17 12 27 44
Which of the following graphs correctly displays the data?
histogram with the title favorite sport and the x axis labeled sport and the y axis labeled number of students, with the first bar labeled basketball going to a value of 17, the second bar labeled baseball going to a value of 12, the third bar labeled soccer going to a value of 27, and the fourth bar labeled tennis going to a value of 44
histogram with the title favorite sport and the x axis labeled sport and the y axis labeled number of students, with the first bar labeled baseball going to a value of 17, the second bar labeled basketball going to a value of 12, the third bar labeled tennis going to a value of 27, and the fourth bar labeled soccer going to a value of 44
bar graph with the title favorite sport and the x axis labeled sport and the y axis labeled number of students, with the first bar labeled basketball going to a value of 17, the second bar labeled baseball going to a value of 12, the third bar labeled soccer going to a value of 27, and the fourth bar labeled tennis going to a value of 44
bar graph with the title favorite sport and the x axis labeled sport and the y axis labeled number of students, with the first bar labeled baseball going to a value of 17, the second bar labeled basketball going to a value of 12, the third bar labeled tennis going to a value of 27, and the fourth bar labeled soccer going to a value of 44
Question 8
A New York City hotel surveyed its visitors to determine which type of transportation they used to get around the city. The hotel created a table of the data it gathered.
Type of Transportation Number of Visitors
Walk 120
Bicycle 24
Car Service 45
Bus 30
Subway 81
Which of the following circle graphs correctly represents the data in the table?
circle graph titled New York City visitor's transportation, with five sections labeled walk 80 percent, bus 16 percent, car service 30 percent, bicycle 20 percent, and subway 54 percent
circle graph titled New York City visitor's transportation, with five sections labeled walk 40 percent, bicycle 8 percent, car service 15 percent, bus 10 percent, and subway 27 percent
circle graph titled New York City visitor's transportation, with five sections labeled subway 40 percent, bus 8 percent, car service 15 percent, bicycle 10 percent, and walk 27 percent
circle graph titled New York City visitor's transportation, with five sections labeled subway 80 percent, bicycle 20 percent, car service 30 percent, bus 16 percent, and walk 54 percent
Question 9
A college cafeteria is looking for a new dessert to offer its 4,000 students. The table shows the preference of 225 students.
Ice Cream Candy Cake Pie Cookies
81 9 72 36 27
Which statement is the best prediction about the scoops of ice cream the college will need?
The college will have about 480 students who prefer ice cream.
The college will have about 640 students who prefer ice cream.
The college will have about 1,280 students who prefer ice cream.
The college will have about 1,440 students who prefer ice cream.
Question 10
The box plots display measures from data collected when 20 people were asked about their wait time at a drive-thru restaurant window.
A horizontal line starting at 0, with tick marks every one-half unit up to 32. The line is labeled Wait Time In Minutes. The box extends from 8.5 to 15.5 on the number line. A line in the box is at 12. The lines outside the box end at 3 and 27. The graph is titled Super Fast Food.
A horizontal line starting at 0, with tick marks every one-half unit up to 32. The line is labeled Wait Time In Minutes. The box extends from 9.5 to 24 on the number line. A line in the box is at 15.5. The lines outside the box end at 2 and 30. The graph is titled Burger Quick.
Which drive-thru typically has more wait time, and why?
Burger Quick, because it has a larger median
Burger Quick, because it has a larger mean
Super Fast Food, because it has a larger median
Super Fast Food, because it has a larger mean
Answers
Answer:
B
B
A
B
D
C
Step-by-step explanation:
5. B
65 = teachers
15 = principal
65/80 = 81.25
If there's is a total of 900 people, find 81.25 (number of teachers)
=731.25
=731
6. B
The best graphical representation for the teacher's data would be a histogram. A histogram is a graph that displays the distribution of continuous data, such as the number of students who prefer a particular subject. It shows the frequency of each interval, or bin, of values.
A stem-and-leaf plot is typically used for small datasets and displays each data point. A circle graph, also known as a pie chart, is used to show how different parts make up a whole and is not appropriate for showing the distribution of preferences among the students. A box plot, also known as a box-and-whisker plot, is used to display the distribution of data, but it may not be as useful for showing the specific frequencies of each preference as a histogram would be.
7) A
There's an image for it I attached
8) B
The correct circle graph that represents the data in the table is option B) circle graph titled New York City visitor's transportation, with five sections labeled walk 40 percent, bicycle 8 percent, car service 15 percent, bus 10 percent, and subway 27 percent.
In the given table, the number of visitors for each type of transportation is given. To create a circle graph, we need to convert the given numbers to percentages. Then, we can use these percentages to determine the angle of each section in the circle graph.
Using the given numbers, we can calculate the percentage of visitors for each transportation type as follows:
Walk: (120/300) x 100 = 40%
Bicycle: (24/300) x 100 = 8%
Car Service: (45/300) x 100 = 15%
Bus: (30/300) x 100 = 10%
Subway: (81/300) x 100 = 27%
Option B) correctly represents these percentages in a circle graph.
9) D
The best prediction about the scoops of ice cream the college will need is option D) The college will have about 1,440 students who prefer ice cream.
To make this prediction, we need to use the information given in the table and assume that the entire student body has the same preferences as the sample of 225 students.
According to the table, 81 out of 225 students prefer ice cream.
To estimate the number of students who prefer ice cream in the entire student body of 4,000 students, we can use proportions.
81/225 = x/4000
Multiplying both sides by 4000, we get:x = 81/225 x 4000 = 1,440
Therefore, the college will have about 1,440 students who prefer ice cream, and they will need to prepare that many scoops.
10) C
The drive-thru that typically has more wait time is option C) Super Fast Food, because it has a larger median.
The median is the middle value when a set of data is arranged in order. In this case, the median wait time for Super Fast Food is 12 minutes, and the median wait time for Burger Quick is 15.5 minutes.
This means that half of the customers at Super Fast Food waited less than 12 minutes, while half of the customers at Burger Quick waited less than 15.5 minutes.
Therefore, the wait time at Super Fast Food is typically shorter than at Burger Quick.
The mean, on the other hand, is influenced by outliers or extreme values, and it is not as robust a measure of central tendency as the median. Therefore, we cannot determine which drive-thru typically has more wait time based on the mean alone.
the anova procedure is a statistical approach for determining whether the means of . a. more than two samples are equal b. two or more populations are equal c. two samples are equal d. two or more samples are equal
Answers
The means of two or more populations being equal is determined by a statistical approach for the ANOVA procedure. Option B is correct.
The ANOVA (Analysis of Variance) procedure is a statistical method used to determine whether there is a significant difference between the means of two or more groups. To statistically test the equality of means ANOVA uses F-tests.
The repeated-measures ANOVA is a two-stage process that is described as an analysis of dependencies. This test is used to prove an assumed cause-effect relationship between variables. The conditions that must be met for the results of an ANOVA are Independence, Random Sampling, Large Sample Size, and Normality.
To learn more about the ANOVA :
https://brainly.com/question/30127764
#SPJ4
it is believed that 5% of all people requesting travel brochures for transatlantic cruises actually take the cruise within 1 year of the request. an experienced travel agent believes this is wrong. of 100 people requesting one of these brochures, only 3 have taken the cruise within 1 year. we want to test the travel agent's theory with a hypothesis test. if you used a significance level of 0.05, what is your decision?
Answers
Based on the given information, we can set up the following hypotheses for the hypothesis test:
Null Hypothesis (H0): The actual proportion of people taking the cruise within 1 year is equal to the believed proportion of 5%.
Alternative Hypothesis (H1): The actual proportion of people taking the cruise within 1 year is not equal to the believed proportion of 5%.
Let p be the proportion of people taking the cruise within 1 year. We can use the sample proportion, denoted as p-hat, which is calculated as the ratio of the number of people who took the cruise within 1 year (3 in this case) to the total number of people who requested the brochures (100 in this case).
Given that the significance level is 0.05, we can use a z-test to compare the sample proportion with the believed proportion of 5%. The z-test statistic is calculated as:
z = (p-hat - p) / sqrt(p * (1 - p) / n)
where n is the sample size, which is 100 in this case.
Now we can calculate the z-test statistic and compare it with the critical value for a two-tailed test at a significance level of 0.05. If the calculated z-test statistic falls outside the critical value, we would reject the null hypothesis; otherwise, we would fail to reject the null hypothesis.
Since the sample proportion p-hat is 3/100 = 0.03, and the believed proportion p is 0.05, we can substitute these values into the z-test formula:
z = (0.03 - 0.05) / sqrt(0.05 * (1 - 0.05) / 100)
Calculating the above expression, we get the value of z. We can then compare this value with the critical value for a two-tailed test at a significance level of 0.05 from a standard normal distribution table or using a statistical calculator.
If the calculated z-test statistic falls outside the critical value, we would reject the null hypothesis and conclude that the actual proportion of people taking the cruise within 1 year is different from the believed proportion of 5%. If the calculated z-test statistic falls within the critical value, we would fail to reject the null hypothesis and not conclude that the actual proportion is different from the believed proportion.
Without the actual values of the calculated z-test statistic and the critical value, we cannot provide a specific decision for this hypothesis test. Please note that hypothesis testing requires careful consideration of the sample size, significance level, and other relevant factors, and should be conducted with caution and in consultation with a qualified statistician or expert in statistical analysis.
When adding or subtracting mixed numbers with like denominators, the numerators ___ , but the denominators ______ .
A. Stay the same
B. change
Answers
Answer:
Yo, when you adding or subtracting mixed numbers with the same denominators, the numerators stay chill, they don't change, bro.
But the denominators, they also stay the same, man. It's like keeping things consistent, ya feel me? So the answer is A, dude. Numerators stay put, denominators stay put. It's all good vibes, bro! ✌️
Any help? Please. Whoever answer it first gets brainliest!
Answers
Answer:
[tex]c + 15 > 24[/tex]
[tex]c > 9[/tex]
The additional amount will be more than $9.
2. Tyler leaves his house at 7:00 a.m. to go to school. He walks for 20 minutes until he reaches his school, 1 mile from his house. The function d gives the distance d(t), in miles, of Tyler from his house t minutes after 7:00 a.m. a. Explain what d(5) = 0.25 means in this context. b. On snowy days, Tyler's school has a 2 hour delayed start time (120 minutes). The function is gives Tyler's distance s(t), in miles, from home t minutes after 7:00 a.m. with a 120 minute delayed start time. If d(5) = 0.25, then what is the corresponding point on the function s? c. Write an expression for s in terms of d. A new function, n, is defined as n(t) = d(t +60) explain what this means in terms of Tyler's distance from school.
Answers
Answer: a. In this context, d(5) = 0.25 means that 5 minutes after 7:00 a.m., Tyler is 0.25 miles away from his house. This is because the function d(t) gives the distance of Tyler from his house t minutes after 7:00 a.m.
b. If d(5) = 0.25, then we know that 5 minutes after 7:00 a.m., Tyler is 0.25 miles away from his house. If there is a 120-minute delayed start time, then Tyler will walk for 20 + 120 = 140 minutes to reach his school. We want to find the corresponding point on the function s, which gives Tyler's distance from home t minutes after 7:00 a.m. with a 120-minute delayed start time. Since Tyler walks the same distance regardless of the delayed start time, we can use the same function for s as we did for d. Therefore, s(145) = 1.25, since Tyler is 1 mile away from his house after walking for 140 minutes and then an additional 5 minutes to account for the delayed start time.
c. Since Tyler walks the same distance regardless of the delayed start time, we can express s(t) in terms of d(t) by adding 120 minutes to the time t. Therefore, s(t) = d(t + 120).
d. The function n(t) = d(t + 60) gives Tyler's distance from his house t minutes after 8:00 a.m. This is because adding 60 minutes to t corresponds to adding one hour to the time, which means that Tyler leaves his house at 8:00 a.m. instead of 7:00 a.m. Therefore, n(t) gives Tyler's distance from school one hour after he leaves his house.
Step-by-step explanation:
which method uses an arithmetic mean to forecast the next period? group of answer choices naive. exponential smoothing. none of the above moving averages. adaptive filtering.
Answers
The method that uses an arithmetic mean to forecast the next period is "moving averages".
Which method is suitable for arithmetic mean?The method that uses an arithmetic mean to forecast the next period is the "moving averages" method.
In this method, the average of the past observations is calculated, and this average is used as the forecast for the next period.
The number of past observations used in the calculation of the moving average depends on the specific variant of the method being used.
Learn more about arithmetic mean
brainly.com/question/13000783
#SPJ11
use the 60 mutual funds in the table above to conduct the hypothesis test. what is the p value? p value is (to 4 decimals)
Answers
Welch's two-sample t-test indicates that the average of Load Return's population is significantly greater than the average of No Load Return's population, with a large effect size.
The null hypothesis (H0) that the two population means are equal is rejected as the p-value (0.005) is less than the chosen significance level (α=0.05). This indicates that the chance of a Type 1 error is small, and the alternative hypothesis (H1) that the average of Load Return's population is greater than the average of No Load Return's population is supported.
The test statistic (T=-2.646) falls outside the 95% critical value accepted range, which further supports the rejection of H0. The effect size (0.68) is considered large, indicating that the difference between the two population means is substantial.
Learn more about p-value
https://brainly.com/question/13786078
#SPJ4
Complete Question:
use the 60 mutual funds in the table below to conduct the hypothesis test. what is the p value? p value is (to 4 decimals)
in a certain health center there are 3 doctors, 8 nurses and 2 physicians. in how many ways one can form a group of 5 members consisting of 1 doctor, 3 nurse and 1 physician.
Answers
Number of ways to select 1 doctor from 3 = 3C1 = 3
Number of ways to select 3 nurses from 8 = 8C3 = (8*7*6)/(3*2*1) = 56
Number of ways to select 1 physician from 2 = 2C1 = 2
Total number of ways to form the group = number of ways to select 1 doctor * number of ways to select 3 nurses * number of ways to select 1 physician
= 3 * 56 * 2
= 336
Therefore, there are 336 ways to form a group of 5 members consisting of 1 doctor, 3 nurses, and 1 physician from a health center that has 3 doctors, 8 nurses, and 2 physicians.
The radius of a circle is 3 centimeters. What is the length of a 45° arc?
Answers
Answer:
2.36 miles
Step-by-step explanation:
radius, r = 3 miles∅ = 45°Length of an arc = ∅/360 * 2πr= 45/360 * 2 * 3.14 * 3= 2.36 miles
you place in a dark bag 24 marbles. 12 marbles are red, 5 marbles are blue and 7 marbles are yellow. you select 2 random marbles (one after the other without putting the first back in). what is the probability that the marbles have the same color?
Answers
The probability of selecting two marbles with the same color is approximately 0.27 or 27%.
To work out the likelihood that the two marbles drawn have similar variety, we can utilize the accompanying advances:
In the first place, we compute the likelihood of drawing a red marble on the principal pick: 12/24 = 1/2.
On the off chance that the main marble drawn is red, there will be 11 red marbles left clinched, out of a sum of 23 marbles. So the likelihood of drawing one more red marble on the subsequent pick is 11/23.
Likewise, in the event that the principal marble drawn is blue, there will be 4 blue marbles left clinched, out of a sum of 23 marbles. So the likelihood of drawing one more blue marble on the subsequent pick is 4/23.
Furthermore, on the off chance that the main marble drawn is yellow, there will be 6 yellow marbles left taken care of, out of a sum of 23 marbles. So the likelihood of drawing one more yellow marble on the subsequent pick is 6/23.
To get the complete likelihood of drawing two marbles of similar variety, we want to add the probabilities of every one of these cases:
(1/2) x (11/23) + (5/24) x (4/23) + (7/24) x (6/23) = 55/138 or roughly 0.398 or 39.8%.
In this way, the likelihood of drawing two marbles of a similar variety is roughly 39.8%.
To learn more about numerical on probability, refer:
https://brainly.com/question/30736519
#SPJ4
A store is offering a 30% discount on shirts. A shirt at the store has an original cost of $25. What is the cost of the shirt, in dollars, after the discount?
Answers
The cost of the shirt, in dollars, after the 30% discount is $17.50.
What is discount?
A discount is a reduction in the price of a product or service that is offered by a seller to a buyer. Discounts can be offered for a variety of reasons, such as to attract customers, increase sales, or clear out inventory. Discounts can be expressed as a percentage or a fixed amount, and they can be applied at the time of purchase or deducted from an invoice or bill. Discounts are often used in sales promotions, marketing campaigns, and loyalty programs to incentivize customers to buy or use a product or service.
If a store is offering a 30% discount on shirts that cost $25 originally, then the discount amount is:
30% of $25 = 0.30 x $25 = $7.50
The discount amount is $7.50, so the new price of the shirt after the discount is:
$25 - $7.50 = $17.50
Therefore, the cost of the shirt, in dollars, after the 30% discount is $17.50.
To know more about discount visit:
https://brainly.com/question/1548141
#SPJ1
HELP!! 10 POINTS
uhm yeah thats all I've got to say
Answers
The correct statement regarding the middle 50% of the data-set is given as follows:
C. The box, from 41 to 56.
What does a box-and-whisker plot shows?A box and whisker plots shows these five features from a data-set, listed as follows:
The minimum non-outlier value.The 25th percentile, which is the median of the bottom 50%.The median, which splits the entire data-set into two halfs, the bottom 50% and the upper 50%.The 75th percentile, which is the median of the upper 50%.The maximum non-outlier value.The box, from the 25th percentile of 41 to the 75th percentile of 56, shows the middle 50% of the data-set.
More can be learned about box plots at https://brainly.com/question/12343132
#SPJ1
Find the distance, d, of AB.
Answers
The distance between A and B is approximately 8.06 units.
In order to find the distance, d, of AB, we need to use the distance formula. The distance formula gives us the distance between two points in a coordinate plane. It is given as:$$d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$$ where (x1, y1) and (x2, y2) are the coordinates of the two points in question.
In this case, A and B are the two points for which we need to find the distance. Let's assume that the coordinates of A are (x1, y1) and the coordinates of B are (x2, y2).
Then the distance formula becomes:
$$d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$$
$$d = \sqrt{((8 + 4) - 2)^2 + ((5 - 1) - 3)^2}$$
$$d = \sqrt{(10 - 2)^2 + (4 - 3)^2}$$
$$d = \sqrt{(8)^2 + (1)^2}$$
$$d = \sqrt{64 + 1}$$
$$d \approx \sqrt{65}$$
$$d \approx 8.06$$
Therefore, the distance between A and B is approximately 8.06 units.
For more such questions on distance, click on:
https://brainly.com/question/26550516
#SPJ8
If f(x) = 5x - 6, which of these is the inverse of f(x)?
A. f^-¹(x) = x/5 +6
B. f^-¹(x) = x/5 -6
C. f^-¹(x) = x+6/5
D. F^-¹(x) = x-6/5
Answers
To find the inverse of a function, we need to swap the positions of x and y and then solve for y. In other words, we replace f(x) with y and then solve for x.
So, let's start by swapping x and y in the function f(x) = 5x - 6:x = 5y - 6
Next, we'll solve this equation for y:
x + 6 = 5y
y = (x + 6)/5
Therefore, the inverse of f(x) is f^-1(x) = (x + 6)/5, which is option C.shuffle a deck of cards and t urn over t he first card. \i\fhat is t he sample space of t his experiment? how many outcomes are in t he event t hat t he first card is a heart?
Answers
If we shuffle a deck of cards ,turn over first card, then
(a) "Sample-Space" of this experiment is set of all 52 cards.
(b) Number of outcomes in event that the first card is a heart is 13 .
Part (a) : The "Sample-Space" of this experiment refers to all possible outcomes that occur when "first-card" from a shuffled deck of cards is turned over.
In a "standard-deck" of 52 playing cards, the sample space consist of all 52 cards, which includes 4 suits (hearts, diamonds, clubs, spades) each with 13 cards (Ace - 10, Jack, Queen, King).
So, the sample space of this experiment will be set of all 52 possible cards that could be turned over as "first-card".
Part (b) : The event that "first-card" is a heart will consist of all outcomes where the first card turned over is a heart.
In a "standard-deck" of 52 "playing-cards", there are 13 hearts (Ace of Hearts, 2 of Hearts, 3 of Hearts, ..., 10 of Hearts, Jack of Hearts, Queen of Hearts, and King of Hearts).
Therefore, there are 13 outcomes in the event .
Learn more about Sample Space here
https://brainly.com/question/30206035
#SPJ4
The given question is incomplete, the complete question is
Shuffle a deck of cards and turn over the first card.
(a) What is the sample space of this experiment?
(b) How many outcomes are in the event that the first card is a heart?
21st term: 3,8,13,18 What is the indicated term
Answers
The 21st term of the sequence 3, 8, 13, 18, .. is 103
To find the indicated term in the sequence, we first need to identify the pattern followed by the sequence. It appears that each term is obtained by adding 5 to the previous term. So, we can write the general formula for the nth term of the arithmetic sequence as
a(n) = a(1) + (n-1)d
where a(1) is the first term of the sequence, d is the common difference, and n is the term number.
In this case, we have:
a(1) = 3 (the first term)
d = 5 (the common difference)
To find the 21st term, we substitute n = 21 in the formula:
a(21) = a(1) + (21-1)d
a(21) = 3 + 20(5)
a(21) = 103
Learn more about arithmetic sequence here
brainly.com/question/16671654
#SPJ4
Three machines are used to produce nails. The table displays the total number of nails produced by the 3 machines
over different lengths of time.
Nail Production with 3 Machines
Time (minutes)
Number of Nails
(thousands)
15
16
45
48
55
593
ON
If each machine produces nails at the same rate, how many nails can 1 machine produce in 1 hour?
nails
Answers
One machine can produce 600,000 nails in one hour.
Finding the total number of nails produced by the three machines in a minute and dividing that number by three to obtain the number of nails produced by a single machine in a minute are the first two steps in the solution to this problem.
The number of nails produced by a single machine in an hour can then be calculated by multiplying that number by 60.
Now, we add up the total number of nails produced during :
(15 + 16 + 45 + 48 + 55 + 59 + 3) / 7 = 30
To find the number of nails produced by one machine in one hour, we multiply by 60: 10,000 x 60 = 600,000
To know more about multiplying, here
brainly.com/question/30875464
#SPJ4
In triangle ∆ABC, m<A = 33°, m<C = 58°, and AB = 25 in. What is AC to the nearest tenth of an inch?
1. 16.1 in.
2. 38.9 in
3. 42 in.
4. 12 in.
Answers
The length of AC using the laws of sines is 29.5 inches
Calculating the length of ACWe can use the law of sines to solve this problem.
The law of sines states that in any triangle ∆ABC:
a/sin(A) = b/sin(B) = c/sin(C)
where a, b, and c are the lengths of the sides opposite to the angles A, B, and C, respectively.
In this case, we know that m<A = 33°, m<C = 58°, and AB = 25 in.
We need to find AC, which is opposite to angle A.
Let's use the law of sines to solve for AC:
AC/sin(B) = AB/sin(C)
Where
B = 180 - 33 - 58
B = 89
So, we have
AC/sin(89°) = 25/sin(58°)
This gives
AC = 29.5 in. (rounded to the nearest tenth)
Therefore, the answer is 29.5 inches
Read more about triangles at
https://brainly.com/question/19387653
#SPJ1
we have studied srs and stratified sampling, and have also mentioned cluster sampling. there is one more sampling method which arises frequently, called systematic sampling. this is how it works in its simplest form:
Answers
Systematic sampling is a type of probability sampling method where every nth item in a population is selected for inclusion in the sample.
For example, if a researcher wanted to select a systematic sample of 100 students from a school population of 1,000 students, they would randomly select one of the first 10 students (1/10th of the population) and then select every 10th student thereafter until they reach 100. Systematic sampling is often used when the population is too large to enumerate and it is more efficient than simple random sampling. However, it is important to ensure that the sampling interval is not biased in any way, otherwise the sample may not be representative of the population.
Learn about more inclusion here:
https://brainly.com/question/22302092
#SPJ11
Systematic sampling is a relatively easy and quick method of sampling, as it requires less effort and time than other methods such as stratified or cluster sampling.
The starting point is truly random, and that the interval selected does not create any bias in the sample.
Systematic sampling is a method of selecting a sample from a population using a system or a pattern.
It involves selecting every nth item or person from the population after a random starting point has been determined.
To perform systematic sampling, the first item or individual in the sample is randomly selected from the population.
Then, the remaining items or individuals are selected at regular intervals, such as every 10th or 20th item or individual.
The interval is calculated by dividing the population size by the desired sample size.
A researcher wants to select a sample of 100 from a population of 1000, the interval would be. [tex]1000/100 = 10.[/tex]
The researcher would randomly select the first item or individual from the population, and then select every 10th item or individual thereafter until the desired sample size is reached.
For similar questions on Systematic sampling
https://brainly.com/question/28505229
#SPJ11
given: weight a: 140 pounds at 17 inches aft of datum weight b: 120 pounds at 110 inches aft of datum weight c: 85 pounds at 210 inches aft of datum based on this information, the cg would be located how far aft of datum?
Answers
The center of gravity is located 96.7 inches aft of the datum.
To determine the location of the center of gravity (CG) of the system, we need to calculate the moment of each weight about the datum, and then divide the sum of the moments by the total weight of the system.
The moment of each weight is equal to its weight multiplied by its distance from the datum. In this case:
Moment of weight a = 140 pounds x 17 inches = 2,380 inch-pounds
Moment of weight b = 120 pounds x 110 inches = 13,200 inch-pounds
Moment of weight c = 85 pounds x 210 inches = 17,850 inch-pounds
The total weight of the system is:
Total weight = weight a + weight b + weight c = 140 + 120 + 85 = 345 pounds
Therefore, the location of the CG can be calculated as follows:
CG location = (Moment of weight a + Moment of weight b + Moment of weight c) / Total weight
CG location = (2,380 + 13,200 + 17,850) / 345
CG location = 33,430 / 345
CG location = 96.7 inches aft of datum
As a result, the center of gravity is 96.7 inches aft of the datum.
To know more about the Datum, here
https://brainly.com/question/15138411
#SPJ4
find the smallest which 108 must be multiplied to get a perfect square
Answers
Answer:
The answer is 3
Step-by-step explanation:
x×108=y
x×2²×3³=y
3×108=324