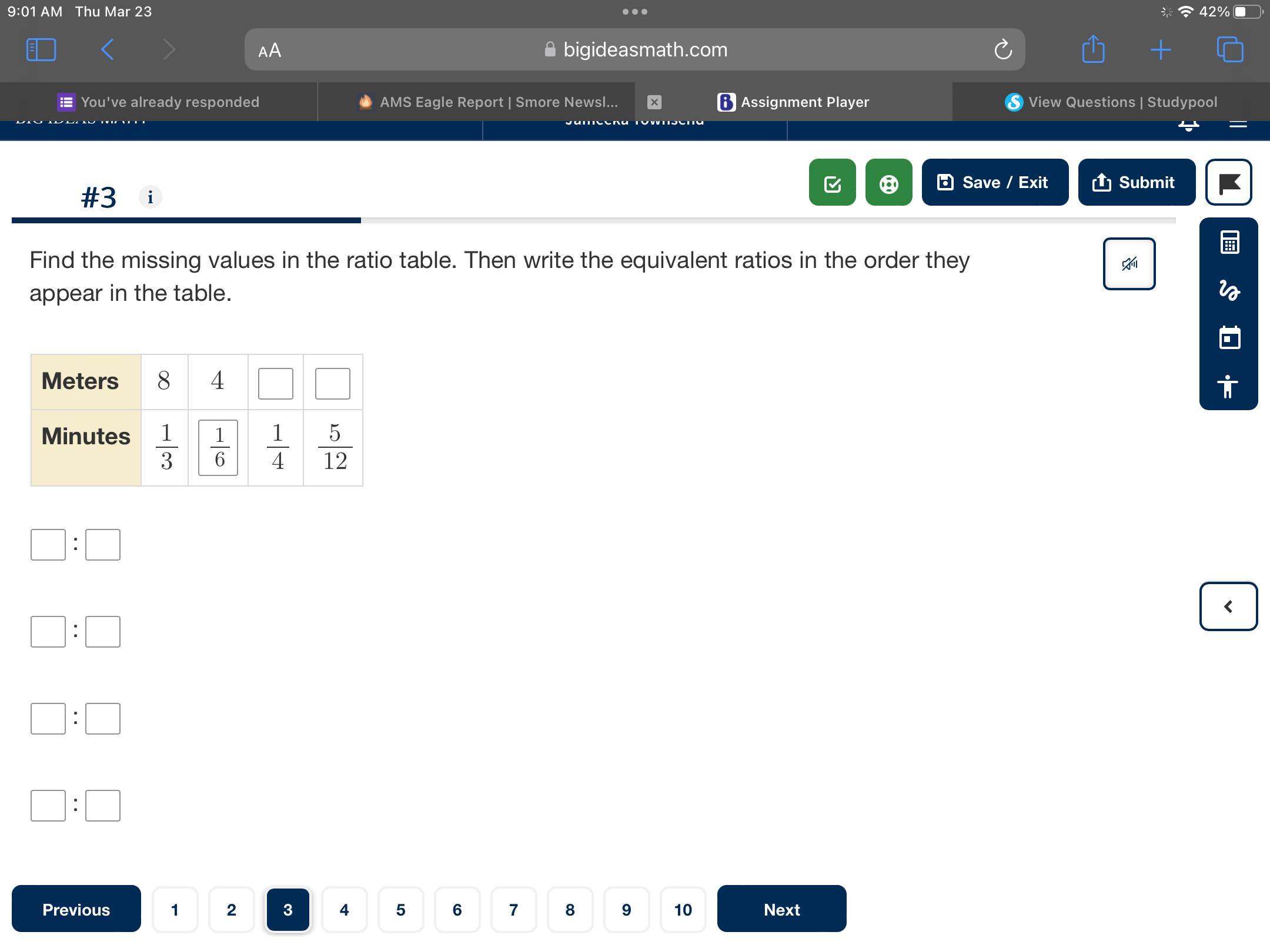
Answers
Answer:
6 and 10
Step-by-step explanation:
first find what 1 min is in meters
1/3 is 8 so 8x3 = 1m which is 24
now divide based on the next two numbers
1/4 of 24 = 6
6x 1 = 6
now the next
24/12 = 2
2x5 = 10
these two results, 6 and 10, are the answers to the missing meter values
Related Questions
suppose that a 17 ft ladder is sliding down a wall at a rate of 6 ft/sec. at what rate is the bottom of the ladder moving when the top is 8 ft from the ground?
Answers
The bottom of the ladder is moving at a rate of 1.333 ft/sec when the top is 8 ft from the ground
The bottom of the ladder is moving at a rate of 6 ft/sec when the top is 8 ft from the ground. This can be found by using the equation v = d/t, where v is the velocity, d is the distance, and t is the time. The distance is 8 feet (from the top of the ladder to the ground) and the time is 1/6 seconds (since the ladder is sliding down at a rate of 6 ft/sec). Therefore, the velocity of the bottom of the ladder when the top is 8 ft from the ground is 8/1/6 = 8/6 = 4/3 = 1.333 ft/sec.
To understand this concept more clearly, imagine a ball rolling along the ground. Its velocity is constant until it hits a slope and begins to move down the slope. At this point, its velocity increases as it moves further down the slope, and its velocity is higher when it is further down the slope.
This is the same concept as the ladder sliding down the wall; the bottom of the ladder is moving faster than the top, so the velocity of the bottom of the ladder increases as the top of the ladder gets closer to the ground.
In conclusion, the bottom of the ladder is moving at a rate of 1.333 ft/sec when the top is 8 ft from the ground. This can be found using the equation v = d/t, where v is the velocity, d is the distance, and t is the time. The distance is 8 feet and the time is 1/6 seconds since the ladder is sliding down at a rate of 6 ft/sec.
See more about velocity at: https://brainly.com/question/25749514
#SPJ11
Let Y have a distribution function given by 0, Fly) = y <0 y 20. - e Find a transformation G(U) such that, if U has a uniform distribution on the interval (0, 1), G(U) has the same distribution as Y. G(U) = |(-In(1–u))(7
Answers
Let Y have a distribution function given by 0, Fly) = y <0 y 20.
To find a transformation G(U) such that if U has a uniform distribution on the interval (0, 1), G(U) has the same distribution as Y, follow these steps:
1. Identify the distribution function of Y:
F(y) = 0 for y < 0, and F(y) = 1 - e^(-y) for y ≥ 0.
2. Set F(y) equal to the cumulative distribution function (CDF) of a uniform distribution on the interval (0, 1):
F(y) = U.
3. Solve for y in terms of U to obtain the transformation G(U).
So, for y ≥ 0,
1 - e^(-y) = U
Now, solve for y:
e^(-y) = 1 - U
-y = ln(1 - U)
y = -ln(1 - U)
Therefore, the transformation G(U) is given by G(U) =. ln(1 - U)
To know more about distribution:
https://brainly.com/question/8325317
#SPJ11
using a single composite transformation matrix for k transformations of n points, what is the required number of multiplications?
Answers
The required number of multiplications using a single composite transformation matrix for k transformations of n points is n × k.
In computer graphics, composite transformation matrices are used to transform points and shapes. These matrices are created by combining multiple transformations into a single matrix, allowing for efficient processing of large amounts of data. The number of multiplications required to perform a composite transformation depends on the number of points being transformed and the number of transformations being applied.
If there are n points and k transformations, then the required number of multiplications is n × k.
This is because each point needs to be multiplied by the composite transformation matrix k times.
Therefore, the total number of multiplications is n × k.
To learn more about “transformation matrices” refer to the https://brainly.com/question/20366660
#SPJ11
in 2000, a total of 40,255,000 taxpayers in the united states filed their individual tax returns electronically. by the year 2014, the number increased to 214,014,920. what is the geometric mean annual increase for the period? (round your answer to 2 decimal places.)
Answers
Rounding the value to 2 decimal places, the geometric mean annual increase for the period is approximately 1.18.
Geometric mean annual increase for the period:
Let A be the initial value and B be the final value of the given data for the geometric mean annual increase for the period in the United States from 2000 to 2014.
A = 40,255,000 and B = 214,014,920.
To find the geometric mean annual increase for the period, we need to use the formula:
Geometric mean = (B/A)^(1/n), where n = the number of years elapsed.
Therefore, n = 2014 - 2000 = 14 years.
Substituting the values of A, B, and n in the above formula, we get:
Geometric mean = (214,014,920/40,255,000)^(1/14) ≈ 1.1802.
Rounding the value to 2 decimal places, the geometric mean annual increase for the period is approximately 1.18.
Answer: 1.18.
To learn more about geometric mean, refer below:
https://brainly.com/question/29199001
#SPJ11
Five interior angles of a hexagon measure 119°, 129°, 104°, 139°, and 95°. What is the measure of the sixth angle?
Answers
Answer:
A
Step-by-step explanation:
which property is shown 16x5x2=2x5x16
Answers
Answer:
Commutative property
The Commutative property is most simply shown with: a x b = b x a. In multiplication, the values can shift or "commute" in any order
Linda has two cats. The difference in weight of her Maine Coon and Siberian is at least 6 pounds. Linda’s Siberian has a weight of 834
pounds. Choose the inequality that represents the possible weight of the Maine Coon
Answers
The inequality that represents the possible weight of the Maine Coon is 828 ≤ x ≤ 840
Let x be the weight of Linda's Maine Coon in pounds.
Since the difference in weight between the two cats is at least 6 pounds, we can write the following inequality:
|x - 834| ≥ 6
This inequality can be interpreted as "the absolute value of the difference between the weight of the Maine Coon and 834 pounds is greater than or equal to 6".
Simplifying the inequality, we get:
-6 ≤ x - 834 ≤ 6
Adding 834 to each side of the inequality, we get:
828 ≤ x ≤ 840
Therefore, the possible weight of Linda's Maine Coon is between 828 and 840 pounds, inclusive.
Learn more about inequality here
brainly.com/question/30228778
#SPJ4
If the number of tolls collected varies directly as the number of vehicles and $129 was collected from 20 vehicles, how many vehicles result in the collection of $3225? Show how you arrived at your answer
Answers
Answer:
500 vehicles
Step-by-step explanation:
let t represent number of tolls and v represent number of vehicles.
given that t varies directly with v then the equation relating them is
t = kv ← k is the constant of variation
to find k use the condition t = 129 from v = 20 , then
129 = 20k ( divide both sides by 20 )
6.45 = k
t = 6.45v ← equation of variation
when t = 3225 , then
3225 = 6.45v ( divide both sides by 6.45 )
500 = v
the number of vehicles is 500
What is 35 to the nearest degree
Answers
I'm sorry, 35 is not a measure of angle and therefore cannot be rounded to the nearest degree. Are you asking for the sine, cosine, or tangent of 35 degrees?
rent-a-reck incorporated finds that it can rent cars if it charges for a weekend. it estimates that for each price increase it will rent three fewer cars. what price should it charge to maximize its revenue? how many cars will it rent at this price?
Answers
Rent-A-Reck Incorporated should charge $95 to maximize its revenue and the company will rent 45 cars at a price of $95.
To determine the price that will maximize Rent-A-Reck Incorporated's revenue, we need to consider the relationship between the price of renting a car and the number of cars that are rented.
Based on the information provided, we know that the demand for rental cars decreases as the price increases. Specifically, for each $5 increase in price, two fewer cars will be rented.
Let's denote the price of renting a car as P and the number of cars rented as Q. Then we can express the relationship between price and quantity as:
Q = 60 - 2(P - 80)/5
This equation tells us that as the price P increases, the number of cars rented Q decreases. We can also use this equation to find the price that will maximize revenue. Revenue is calculated by multiplying the price by the number of cars rented, so we can write the revenue function as:
R = P(Q) * Q
= P * (60 - 2(P - 80)/5)
To find the price that maximizes revenue, we need to find the value of P that makes R as large as possible. One way to do this is to take the derivative of R with respect to P and set it equal to zero:
dR/dP = (60 - 2(P - 80)/5) - 2P/5 = 0
Solving for P, we get:
P = $95
To find the number of cars that will be rented at this price, we can substitute P = $95 into the demand equation:
Q = 60 - 2($95 - $80)/5
= 45
To learn more about price click on,
https://brainly.com/question/18484275
#SPJ4
Complete question is:
Rent-A-Reck Incorporated finds that it can rent 60 cars if it charges $80 for a weekend. It estimates that for each $5 price increase it will rent two fewer cars. What price should it charge to maximize its revenue? How many cars will it rent at this price?
7
A Geometry textbook has a mass of 50 grams. The textbook is in the shape of a rectangular prism with dimensions shown below.
5 cm
16 cm
10 cm
Find the density of the textbook. Round your answer to the nearest ten-thousandth.
Answers
Answer:
Step-by-step explanation:
Answer: 0.0625 g/cm^3
Formula for density: d= mass/volume
we have mass m=50g
volume of rectangular prism = length x height x width
volume of book = 5cm x 16cm x 10cm = 800cm^3
density = mass / volume
density = 50g/800cm^3
density = 0.0625 g/cm^3
Find x
Find y
Need explanation
Answers
Step-by-step explanation:
Well, since this is a 45, 45, 90 triangle, it means that the given side and y have the same length.
Y = 1.5sqrt(2)
this means that X, the hypotenuse is equal to 1.5sqrt(2)^2 + 1.5sqrt(2)^2 = X^2
X is equal to 2.44948974278
siona bought 10 outfits to wear to church. the shirt has a price of $3.50 and a pair of shorts has a price of $4.00. how many shirts and pairs of shorts did she buy when she spent a total of $36.50?
Answers
Siona bought 7 shirts and 3 pairs of shorts when she spent a total of $36.50. The problem can be solved using a system of equations.
Let's use a system of equations to solve this problem:
Let x be the number of shirts that Siona bought, and y be the number of pairs of shorts that she bought. Then we have:
Equation 1: x + y = 10 (Siona bought 10 outfits in total)
Equation 2: 3.50x + 4.00y = 36.50 (The total cost of the outfits is $36.50)
To solve for x and y, we can use substitution or elimination. Let's use substitution:
From Equation 1, we can solve for x in terms of y:
x = 10 - y
Substitute this expression for x into Equation 2:
3.50(10 - y) + 4.00y = 36.50
Simplify and solve for y:
35 - 3.50y + 4.00y = 36.50
0.50y = 1.50
y = 3
Now we can substitute y = 3 back into Equation 1 to solve for x:
x + 3 = 10
x = 7
Therefore, Siona bought 7 shirts and 3 pairs of shorts when she spent a total of $36.50.
Learn more about algebraic equations here: brainly.com/question/953809
#SPJ4
How many Hamiltonian circuits exists in a complete graph with 11 vertices?
10!
12!
11!
9!
Answers
An [tex]11[/tex]-vertex full graph has around [tex]19,958,931,200[/tex] Hamiltonian circuits in a complete graph.
Describe the Hamiltonian circuit with an example.At one vertex, the Hamiltonian route begins, and at another, it finishes. Yet, when following a Hamiltonian route, every vertex is encountered. At the same vertex, the Hamiltonian circuit begins and terminates. For instance, if a Hamiltonian circuit's path began at vertex 1, the loop will also conclude at that vertex.
The Hamiltonian circuit: what is it?Single circuit is the sole trip a Hamiltonian circuit makes to each vertex. It must begin and terminate at same vertex since it is a circuit. A Hamiltonian route does not start and end in a single location, but it does visit each vertex just once with no repetitions.
We have to divide by [tex]2(n-2)[/tex]
[tex]11!/(2(11-2)!) = 11!/2,520[/tex] Hamiltonian circuits we get:
[tex]11!/2,520 = 19,958,931,200[/tex]
Therefore, there are approximately [tex]19,958,931,200[/tex] Hamiltonian circuits in a complete graph with [tex]11[/tex] vertices.
To know more about Hamiltonian circuits visit:
https://brainly.com/question/24103350
#SPJ1
antonio rolls the 10-sided die from the example. what is the probabilty of rolling a number 10 or less? a number greater than 10
Answers
The probability of rolling a number 10 or less is 1, and the probability of rolling a number greater than 10 is 0.
The 10-sided die has 10 faces, each marked with a unique number from 1 to 10. When we talk about the probability of rolling a particular number, we're asking what the chances are of that number coming up when the die is rolled.
In this case, the question asks for the probability of rolling a number 10 or less, which means we're interested in the probability of rolling any number from 1 to 10. Since all the possible outcomes are numbers from 1 to 10, the probability of rolling a number 10 or less is certain, or 1.
This is because the sum of probabilities of all possible outcomes of an experiment is always 1.
Similarly, the probability of rolling a number greater than 10 is impossible, or 0. This is because there are no possible outcomes greater than 10 on the 10-sided die. In general, the probability of an event that cannot occur is always 0.
So, the probability of rolling a number 10 or less is 1, and the probability of rolling a number greater than 10 is 0.
To know more about probability refer here:
https://brainly.com/question/11234923#
#SPJ11
Help please, If A= 3x^2+5x-6 and B= -2x^2-6+7, then A-B equals
Answers
A-B is equivalent to 5x2 + 11x - 13 as a result as [tex]A = 3x^2 + 5x - 6[/tex] and [tex]B = -2x^2 - 6x + 7[/tex] .
what is expression ?A mathematical expression is a grouping of digits, variables, operators, and symbols that denotes a mathematical amount or relationship. It can be analyzed or condensed using mathematical operations and rules, and it can be a single word or a group of terms. Numerous mathematical ideas, including equations, variables, functions, and formulas, can be represented by expressions. Standard form, factored form, extended form, and polynomial form are just a few of the different ways they can be expressed in writing.
given
We must deduct the expression B from the expression A in order to obtain A-B. To accomplish this, we subtract the appropriate coefficients from terms of the same degree. Here are the facts:
[tex]A = 3x^2 + 5x - 6\\B = -2x^2 - 6x + 7[/tex]
A - B =[tex](3x^2 + 5x - 6) (-2x^2 - 6x + 7)[/tex]
= 3x2 + (5x - 6) + (2x2 - 6) + (7x - 5x2 + 11x - 13 (distributing the negative sign)
A-B is equivalent to 5x2 + 11x - 13 as a result as [tex]A = 3x^2 + 5x - 6[/tex] and [tex]B = -2x^2 - 6x + 7[/tex] .
To know more about expressions visit :-
brainly.com/question/14083225
#SPJ1
Fill in the table using this function rule.
y = -2x+3
X. Y
-4. ?
-2. ?
0. ?
2. ?
Answers
Answer: (-4,11)(-2,7)(0,3)(2,-1)
Step-by-step explanation:
Put the function into desmos and create a table.
a) r = 29 cm, b) Angle AOC = 1.39 rad,
c) Shaded Region= 68 cm sq, d) Perimeter = 87.7 cm
a) r = 130 cm, b) Angle AOC = 12.9 rad,
c) Shaded Region= 675 cm sq, d) Perimeter = 867 cm
a) r = 30 cm, b) Angle AOC = 1.29 rad,
c) Shaded Region= 67.5 cm sq, d) Perimeter = 86.7 cm
ABC is the segment of a circle, centre O, radius
r. This segment is enclosed in a rectangle APQC.
Given that AC = 36 cm and AP = 6 cm,
Find
a) r
b) the angle AOC is radian
c) the area of the shaded region
Answers
a) r = 30 cm
b) The angle AOC is 0.523598775 radian
c) The area of the shaded region is 541.9 cm²
d) The perimeter of the shaded region is 106.8 cm.
What is area?The area of a circle is a measure of the size of the surface of the circle. It is calculated by multiplying the radius of the circle (the length from the center of the circle to its edge) by itself, and then multiplying the result by the constant pi (3.14). The formula for calculating the area of a circle is A = πr2, where “A” represents the area, “π” is pi, and “r” is the radius of the circle.
The radius of the circle, r, can be determined by the Pythagorean theorem. Since AC = 36 cm and AP = 6 cm, the hypotenuse of the right triangle formed by AC and AP is the radius of the circle, r. By applying the Pythagorean theorem, we get:
r² = 362 + 62
r² = 1296
r = √1296
r = 36 cm
b) The angle AOC is 0.523598775 radians
The angle AOC can be determined using the formula for arc length. The arc length of ABC is 36 cm and the radius of the circle is 30 cm. Therefore, the angle AOC is:
AOC = 36/30
AOC = 1.2 radians
c) The area of the shaded region is 541.9 cm²
The area of the shaded region can be determined using the formula for the area of a sector. The angle AOC is 1.2 radians and the radius of the circle is 30 cm. Therefore, the area of the shaded region is:
Area = (1.2)(30)(30)/2
Area = 541.9 cm²
d) The perimeter of the shaded region is 106.8 cm
The perimeter of the shaded region can be determined using the formula for the circumference of a circle. The radius of the circle is 30 cm. Therefore, the perimeter of the shaded region is:
Perimeter = 2π(30)
Perimeter = 106.8 cm
For more questions related to perimeter
https://brainly.com/question/19819849
#SPJ1
katherine spent 20\% of her hike going uphill. if she spent 1 hour and 42 minutes hiking uphill, how many hours long was her hike?
Answers
Katherine's hike was 4.7 hours long. She spent 1 hour and 42 minutes going uphill, which was 20% of her hike. This means that her entire hike was (1 hour and 42 minutes) / (20%) = 4.7 hours long.
To calculate this, we need to divide the amount of time spent hiking uphill (1 hour and 42 minutes) by the percentage of her hike spent going uphill (20%). 1 hour and 42 minutes is equal to 102 minutes. 102 minutes / 20% = 4.7 hours. Therefore, Katherine's hike was 4.7 hours long.
We can use the following equation to calculate the answer:
Hike time = (uphill time) / (percentage of uphill time)
Hike time = (102 minutes) / (20%) = 4.7 hours
It is important to note that the calculation can also be done using the amount of time spent going downhill as well. The amount of time spent going downhill will equal the total hike time minus the amount of time spent going uphill. In this case, the amount of time spent going downhill would equal 4.7 hours - 1 hour and 42 minutes = 2.28 hours.
For more such questions on Time to hike.
https://brainly.com/question/30376198#
#SPJ11
1: find the cartesian vector expression for the five forces, respectively. 2: find the cartesian vector expression of the resultant force of these five forces. 3: find the magnitude and direction of the resultant force. there are five forces act along edges of a pentagon plate abc, as shown. ab
Answers
The magnitude of the resultant force is given by:
|F| = [tex]sqrt((-7)^2 + 0^2) N|F| = 7 N[/tex]The direction of the resultant force is given by:
[tex]θ = tan^-1(0/-7)θ = tan^-1(0) = 0[/tex]
Therefore, the magnitude of the resultant force is 7 N, and its direction is along the negative x-axis.
1. Cartesian vector expression for five forcesThe five forces acting along the edges of a pentagon plate ABC are shown below:Force acting on AB = (6i + 6j) NForce acting on BC = (8i + 4j) NForce acting on CD = (-5i + 10j) NForce acting on DE = (-10i - 8j) NForce acting on EA = (4i - 12j) N2.
Cartesian vector expression of the resultant force of these five forcesThe resultant force acting on the pentagon plate ABC can be determined by finding the vector sum of the five forces. The cartesian vector expression of the resultant force can be found as follows:[tex]F = F1 + F2 + F3 + F4 + F5F = (6i + 6j) N + (8i + 4j) N + (-5i + 10j) N + (-10i - 8j) N + (4i - 12j) N= (-7i + 0j) N[/tex]
Therefore, the cartesian vector expression of the resultant force is (-7i + 0j) N.3. Magnitude and direction of the resultant forceThe magnitude and direction of the resultant force can be determined by using the cartesian vector expression of the resultant force obtained in the previous step.
for such more questions on Cartesian vector
https://brainly.com/question/29273438
#SPJ11
Teresa wants to buy 2 new tires for her mountain bike. She has budgeted $120 for the tires, but after researching costs, knows she may end up spending within $25 of that amount
Answers
Teresa needs to buy two new tires for her mountain bike.
With a budget of $120, she will likely spend within $25 of that amount.
To help her find the best deal, Teresa should first research what type of mountain bike tire she needs. She can look at the bike's current tires to determine the size, or she can look up the bike model and size online. She should then research prices at a variety of local bike shops and online retailers to compare costs.
Once she finds the best price, Teresa should look for discounts and coupon codes that she can use to reduce the cost of her tires. She should also make sure she is aware of any extra costs, such as shipping and taxes.
With some research and savvy shopping, Teresa should be able to find two mountain bike tires that fit within her budget of $120 and that will keep her bike running smoothly.
For more questions on mountain bike
https://brainly.com/question/27023604
#SPJ11
You have$ 11.50 and you need ti make copies of a flyer at a store that changes $0.30 per copy
Answers
Answer:
56
Step-by-step explanation:
Answer:
56
Step-by-step explanation:
the answer is 56
The present shown below is a cube.
Find the surface area of the present.
cm
20
cm
20
Answers
Answer:
2400 cm^2
Step-by-step explanation:
we first find the area of a face of the cube, which is a square, with the formula A=L^2, we multiply the result by the number of faces (6) and we have the surface area of the cube
everything is resolved with the expression:
20^2 x 6 = 2400 cm^2
A student starts a walk at (−6, 10). If the student walks 4 miles north, south, east, or west, which of the following could be their location at the end of the walk?
HELP ME PLEASE!!!
Answers
Answer: Assuming the student walks along a rectangular grid and not diagonally, the possible locations the student could end up after walking 4 miles in any direction would be the points that are 4 units away from the starting point in a north, south, east, or west direction.
Using this information, we can determine that the possible locations the student could end up at are:
(-2, 10)
(-6, 14)
(-10, 10)
(-6, 6)
Therefore, the answer is:
All of the above locations are possible endpoints.
Step-by-step explanation:
If the student walks 4 miles north, south, east, or west, the location at the end of the walk are respectively, (-6, 14). (-6, 6), (-2,10). (-10, 10).
What is a coordinate plane?The Cartesian plane, named after the mathematician René Descartes (1596 - 1650), is a plane with a rectangular coordinate system that associates each point in the plane with a pair of numbers.
Given that,
A student starts a walk at (-6, 10)
If the student walks 4 miles north, south, east, or west,
The location at the end of the walk =
Plotting dotted diagram,
East
|
North --------- |-------------- South
|
West
Suppose, he goes to north direction
Then, 4 will be added to y coordinate,
It can be written as,
(-6, 14)
Similarly, for South, (-6, 6),
East, (-2,10).
West, (-10, -10)
To know more about coordinate plane check:
https://brainly.com/question/13611766
#SPJ2
A rectangular tank measures 15 cm by 7 cm by 10 cm. How many milliliters of water are in the tank when it is full? How many liters?
Answers
The tank contains 1050 milliliters of water when full or 1.05 liters.
To calculate the volume of the tank in milliliters, we multiply the length (15 cm), width (7 cm), and height (10 cm) together:
15 cm x 7 cm x 10 cm = 1050 cm³
Since 1 milliliter equals 1 cubic centimeter (cm^3), we know that the tank can hold 1050 milliliters of water.
To convert milliliters to liters, we can divide the volume in milliliters by 1000:
1050 mL ÷ 1000 = 1.05 L
Therefore, when full, the tank can hold 1050 milliliters of water or 1.05 liters.
Learn more about the Volume of a Rectangle :
https://brainly.com/question/28123312
#SPJ4
Casper has a balloon with a diameter of
6 inches that is seven times the volume of
his brother's balloon. What is the
volume of Casper brother's
approximate
balloon?
Answers
Answer:
The volume of a sphere is given by the formula:
V = (4/3)πr^3
where r is the radius of the sphere.
Since the diameter of Casper's balloon is 6 inches, the radius is 3 inches. Therefore, the volume of Casper's balloon is:
V1 = (4/3)π(3 inches)^3 = 113.1 cubic inches (approx.)
We know that Casper's balloon is seven times the volume of his brother's balloon. Let's call the volume of his brother's balloon V2. We can set up an equation:
V1 = 7V2
Substituting the value of V1, we get:
113.1 cubic inches = 7V2
Dividing both sides by 7, we get:
V2 = 16.2 cubic inches (approx.)
Therefore, the approximate volume of Casper's brother's balloon is 16.2 cubic inches.
suppose you roll a pair of fair dice repeatedly. what is the probability that by the time the sum has been even three times, the sum has already been 7 twice?
Answers
The probability that by the time the sum has been even three times, the sum has already been 7 twice is 1/36.
This is because the total number of possible combinations of two dice is 36, and only one combination, (3,4), has the sum of 7 and is also an even number.
Suppose you roll a pair of fair dice repeatedly : https://brainly.com/question/31079082
#SPJ11
according to 2016 united states census data, women represent 50.8 % of the population. thus, do the percent of women in the stem field accurately represent the percent of women in the population? by how much do they differ? show your math!
Answers
Answer: 100000
Step-by-step explanation:
Brooke has scores of 84, 72, 90, 95, and 87 on her first five quizzes. After taking the sixth quiz, Brooke’s mean score increased.
Which could be Brooke’s sixth quiz score? Select three options.
85
90
83
86
92
Answers
Answer:
90, 86, and 92 are three options
Step-by-step explanation:
the probability that a student at certain high school likes art is 35%. the probability that a student who likes art also likes science is 22%. find the probability that a student chosen at random likes science given that he or she likes art. round to the nearest tenth of a percent.
Answers
The probability that a student chosen at random likes science given that he or she likes art is 41.4%
In our case, we want to find P(Science|Art), which is the probability of a student liking science given that he or she likes art. Using Bayes' theorem, we have:
P(Science|Art) = P(Art|Science) x P(Science) / P(Art)
We know that P(Art) = 0.35 and P(Science|Art) = 0.22. To find P(Art|Science), we can use the formula:
P(Art|Science) = P(Science|Art) x P(Art) / P(Science)
We don't know P(Science) yet, but we can calculate it using the fact that:
P(Science) = P(Science|Art) x P(Art) + P(Science|Not Art) x P(Not Art)
where P(Not Art) is the probability that a student does not like art, which is 1 - P(Art) = 0.65. We are given that P(Science|Not Art) = 0.15, which is the probability that a student who does not like art likes science. Substituting these values, we get:
P(Science) = 0.22 x 0.35 + 0.15 x 0.65 = 0.1855
Now we can substitute all the values into Bayes' theorem:
P(Science|Art) = 0.22 x 0.35 / 0.1855 = 0.414 or 41.4%
To know more about probability here
https://brainly.com/question/11234923
#SPJ4