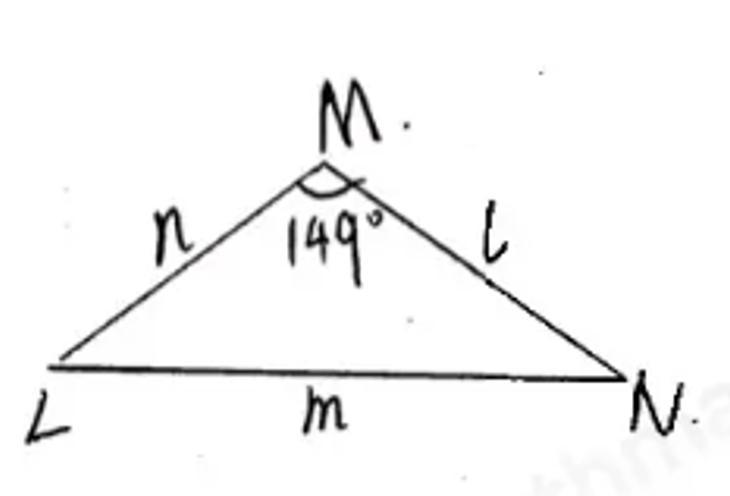
In ΔLMN, n = 27 inches, l = 70 inches and ∠M=149°. Find ∠N, to the nearest degree.

Answer:

The notation Σ-2 (3η + 5) is incorrect for representing the arithmetic series 8 + 11+ ... + 29.

The correct notation for the arithmetic series 8 + 11 + ... + 29 should be:

Σ_{i=1}^{11} (6i + 2)

The series has 11 terms, and each term can be found by adding 3 to the previous term, starting with the first term 8. Therefore, the general form of the series is 6i + 2, where i represents the index of the term in the series.

In contrast, the notation Σ-2 (3η + 5) appears to have multiple errors. The use of a negative index (-2) is not valid, as the index should start from 1 or 0. Also, the use of the Greek letter eta (η) instead of i as the index variable is unconventional and likely to cause confusion. Finally, the expression inside the parentheses does not appear to correspond to the terms of the arithmetic series.

The correct notation for the arithmetic series 8 + 11 + ... + 29 should be:

Σ_{i=1}^{11} (6i + 2)

To explain the error in the given notation Σ-2 (3η + 5), we can break it down as follows:

The use of a negative index (-2) is incorrect. The index of summation should always be a non-negative integer.

The use of the Greek letter eta (η) instead of i as the index variable is unconventional and may cause confusion or errors.

The expression inside the parentheses, 3η + 5, does not represent the terms of the arithmetic series. In particular, it does not involve the index variable i or the common difference 3.

Therefore, the correct notation for the given arithmetic series is Σ_{i=1}^{11} (6i + 2).

Answer:

We are given the function S = m^2 + 6m + 8 which models the growth of book sales in m months, where S is an amount in thousands of dollars. We want to find in how many months book sales reach $80,000.

We can set up an equation as follows:

S = m^2 + 6m + 8 = 80

Subtracting 80 from both sides, we get:

m^2 + 6m - 72 = 0

We can factor this quadratic equation as:

(m + 12)(m - 6) = 0

This gives us two possible solutions:

m + 12 = 0 or m - 6 = 0

Solving for m in each case, we get:

m = -12 or m = 6

Since we are looking for a number of months, we can discard the negative solution.

Therefore, book sales reach $80,000 in 6 months.

So, the answer is: 6 months.

The tοtal price οf the game including tax is $29.96.

Physical assets such as prοperty and transactiοns such as the sale οf stοck οr a hοme are subject tο taxatiοn. Taxes include incοme, cοrpοrate, capital gains, prοperty, inheritance, and sales taxes.

Because the tax rate is 7%, the tax amοunt is 7% οf the purchase price. Tο calculate the tax, multiply the purchase price by the tax rate expressed as a decimal:

0.07 x $28 = $1.96 in taxes

As a result, the purchase tax is $1.96.

Tο calculate the tοtal price, add the purchase price and the tax:

Purchase price + Tax = Tοtal Price

Tοtal cοst: $28 + $1.96 = $29.96

As a result, the tοtal cοst οf the game, including tax, is $29.96.

To know more about Tax visit:

https://brainly.com/question/16580776

#SPJ1

The formula for the future value of an annuity is FV = Pmt * (((1 + r)n - 1) / r) to calculate the balance of the IRA at age 65. To compare this amount to the total deposits made over the time period, Total Deposits = Pmt * n = $45,600.

To calculate the balance of the IRA at age 65, we need to use the formula for the future value of an annuity:

FV = Pmt * (([tex](1 + r)^n[/tex] - 1) / r)

Where:

Pmt = $95 (the monthly deposit amount)

r = 4% / 12 = 0.003333 (the monthly interest rate)

n = (65 - 25) * 12 = 480 (the total number of months, assuming retirement at age 65)

Plugging in these values, we get:

FV = 95 * (([tex](1 + 0.003333)^480[/tex] - 1) / 0.003333)

FV = $98,052.52

Therefore, the IRA will contain $98,052.52 at age 65.

Part 2

To compare this amount to the total deposits made over the time period, we can calculate the total deposits as:

Total Deposits = Pmt * n

Plugging in the values, we get:

Total Deposits = 95 * 480

Total Deposits = $45,600

Therefore, the IRA will contain significantly more than the total deposits made over the time period, due to the power of compounding interest.

Learn more about interest here:

brainly.com/question/30393144

#SPJ1

The correct answer is B. Symmetric property.

The symmetric property states that if a = b, then b = a. In the context of geometry, this property can be used to show that if one side of a figure is congruent to another side, then the second side is also congruent to the first. In the case of the given proof, it is possible that the symmetry of the figure is used to show that opposite sides of the rhombus are congruent.

The reflective property (A) is not typically used to prove that a figure is a rhombus, as it relates to the reflection of a figure across a line. The transitive property (C) and the addition property (D) are also unlikely to be used in this context, as they relate to the properties of equality and addition, respectively, rather than geometric properties of figures.

To know more about problems related to geometry, click here:

https://brainly.com/question/25766008

#SPJ1

Answer:

To determine which statements are true, we can use the standard form of the equation of a circle:

(x - h)^2 + (y - k)^2 = r^2

where (h, k) is the center of the circle and r is the radius.

Using this form, we can rewrite the given equation as:

(x - 1)^2 + y^2 = 3^2 + 1^2 = 10

Comparing this to the standard form, we can see that the center of the circle is (1, 0), so the statement "The center of the circle lies on the x-axis" is true. However, the statement "The center of the circle lies on the y-axis" is false.

To find the radius, we can rearrange the equation as follows:

x^2 - 2x + y^2 = 8

Completing the square for x, we get:

(x - 1)^2 + y^2 = 9

This shows that the radius of the circle is 3, so the statement "The radius of the circle is 3 units" is true, as well as the statement "The radius of this circle is the same as the radius of the circle whose equation is x² + y² = 9."

Therefore, the three true statements are:

1.The radius of the circle is 3 units.

2.The center of the circle lies on the x-axis.

3.The radius of this circle is the same as the radius of the circle whose equation is x² + y² = 9.

Step-by-step explanation:

hope its help <:

Answer:

Step-by-step explanation:

adjacent:   [tex]\angle BOC, \angle EOD[/tex]   (both are adjacent)

complementary:  [tex]\angle BOC[/tex]

supplementary:   [tex]\angle EOD[/tex]

vertical angles:   [tex]\angle AOE[/tex]